Five More Clusters of Rhombicosidodecahedra

Posted on 11 June 2015 by RobertLovesPi

Making the four different clusters of rhombicosidodecahedra seen in the post right before this one was fun, so I decided to make more of them.

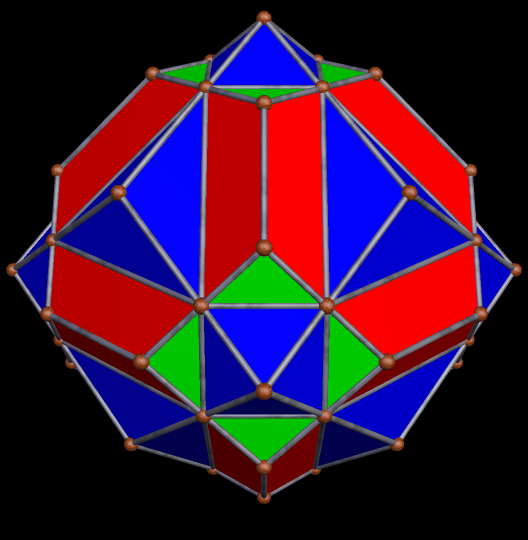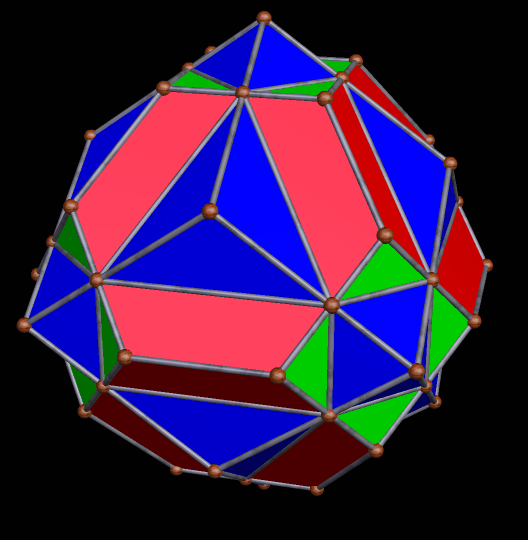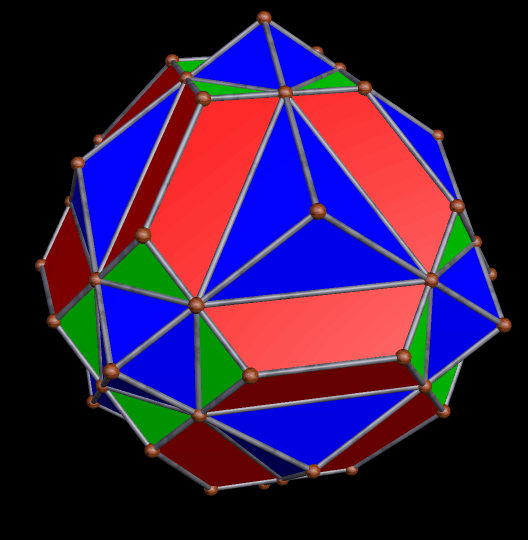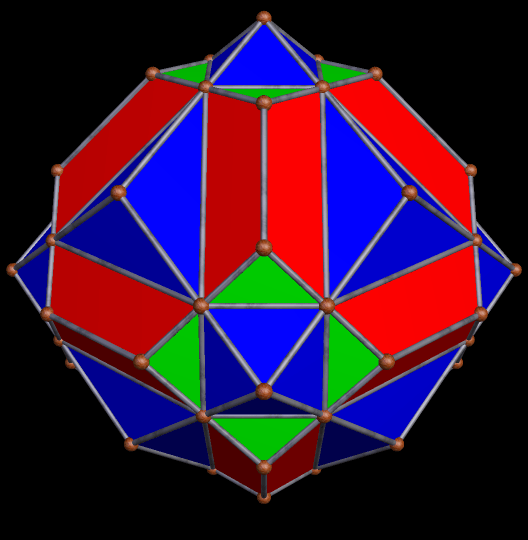
There are two different forms of the compound of twenty tetrahedra. To make the polyhedral cluster above, I chose one of them, and then augmented each of its 20(4) = 80 triangular faces with a rhombicosidodecahedron.

For the next of these clusters, I decided to move away from using compounds for the central, hidden figure. Instead, I chose a snub cube, and augmented each of its 32 triangular faces with a rhombicosidodecahedron. Since the snub cube is chiral, this cluster is chiral as well.

Any chiral polyhedron can be combined with its mirror-image to produce a new compound, and that’s what I did to make this next cluster, which is composed of 64 rhombicosidodecahedra: I simply added the cluster above to its own reflection.

Next, I turned to the snub dodecahedron, also chiral, and with 80 triangular faces. Augmentation of all 80 produced this chiral cluster of 80 rhombicosidodecahedra:

Finally, I added this last cluster to its own mirror-image, producing this symmetrical cluster of 160 rhombicosidodecahedra.

Each of these was created using a program called Stella 4d: Polyhedron Navigator, software you can try for free right here.

Four Different Clusters of Multiple Rhombicosidodecahedra

Posted on 11 June 2015 by RobertLovesPi

To make the cluster above, I began with the compound of five octahedra, which has 5(8) = 40 faces, all of them equilateral triangles. Next, I augmented each of those triangular faces with a single rhombicosidodecahedron — forty in all.

Next, I started anew with the compound of five dodecahedra, which has 5(12) = 60 pentagonal faces, all of them regular. Each of these sixty pentagons was then augmented by a single rhombicosidodecahedron.

For the next cluster, I started with the most well-known compound of ten tetrahedra. There are actually two such compounds; I used the one which is the compound of the chiral five-tetrahedron compound, combined with its mirror image. Since 10(4) = 40, this cluster, like the first one in this post, contains forty rhombicosidodecahedra. Unlike the other models shown here, this one has “holes,” which you can see as it rotates, but the reason for this is a mystery to me. The same is true for the first cluster shown in this post.

There also exist two compounds of eight tetrahedra each, and I used one of them for this next cluster, using the same procedure, so this cluster is composed of 8(4) = 32 rhombicosidodecahedra.