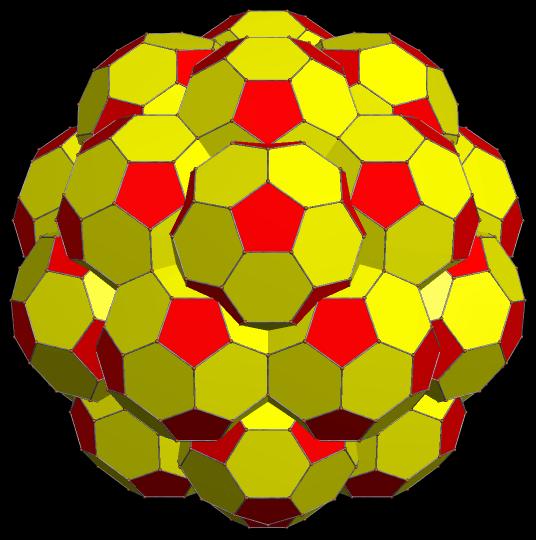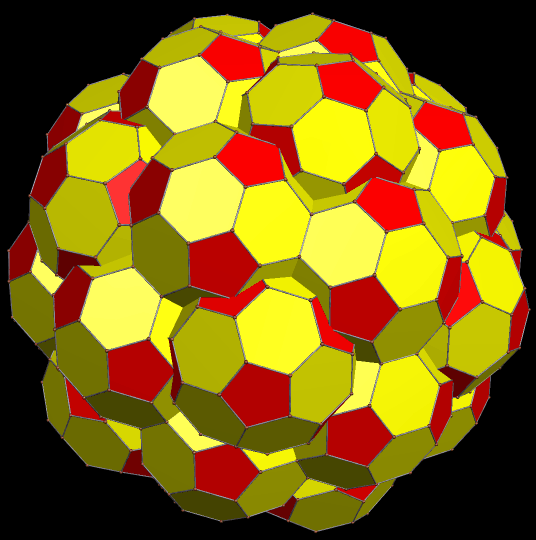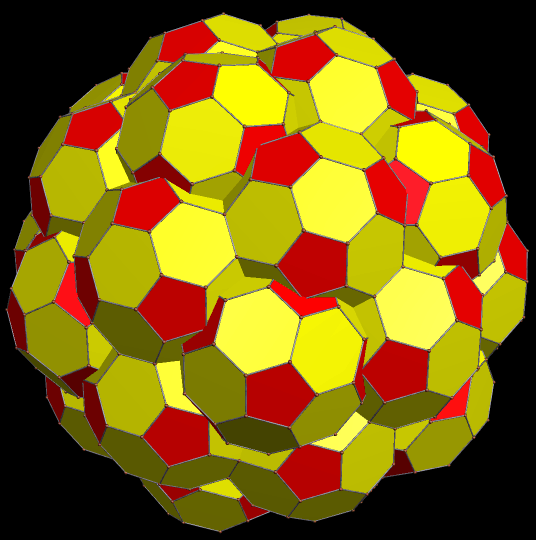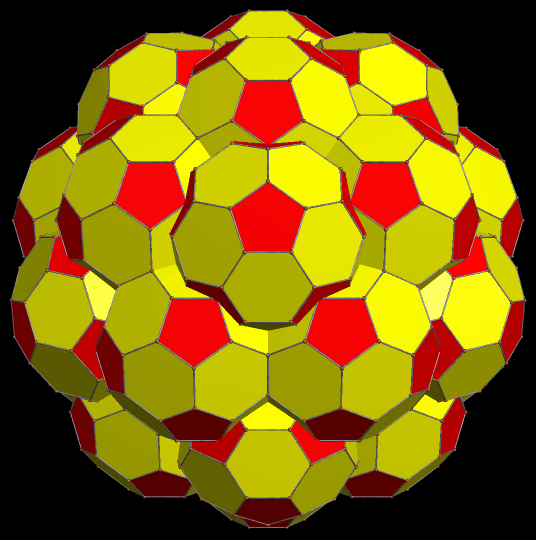
There is one truncated icosahedron at the center of this cluster, and each of its 32 faces is augmented with another truncated icosahedron, for a total of 33. I built this cluster using Stella 4d, software available here.
Monthly Archives: November 2015
A Box of Heptagons
It is hard to find polyhedra which contain regular heptagons, but that simply makes the search more challenging, and therefore more fun. This polyhedron features six regular heptagons, and was created with Stella 4d, software available here.
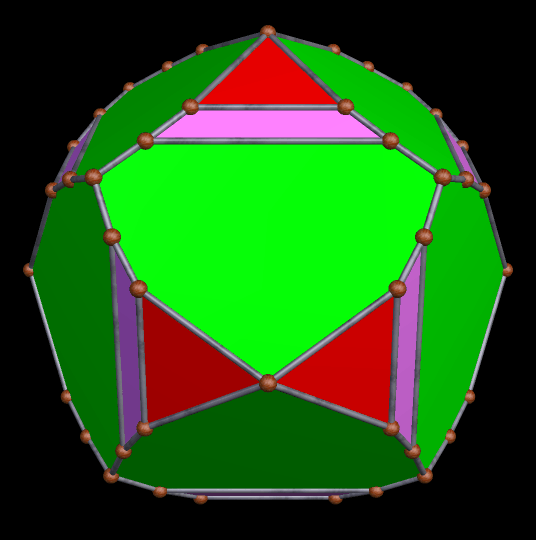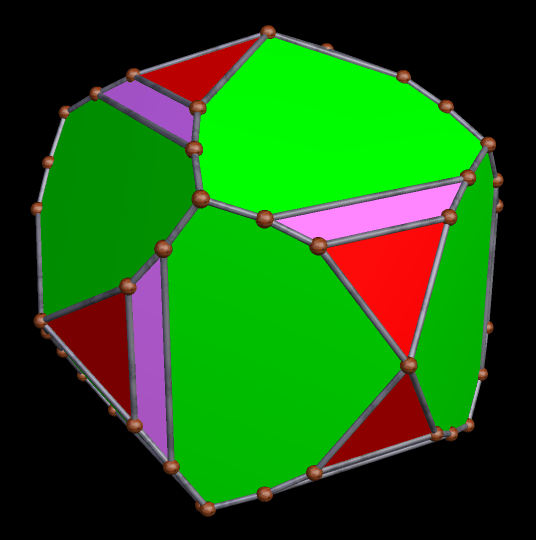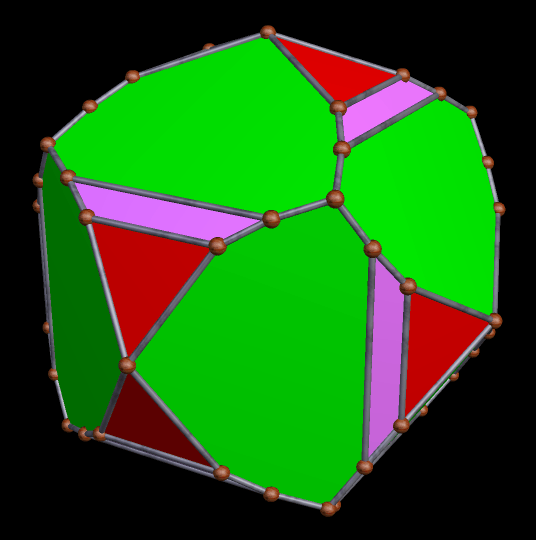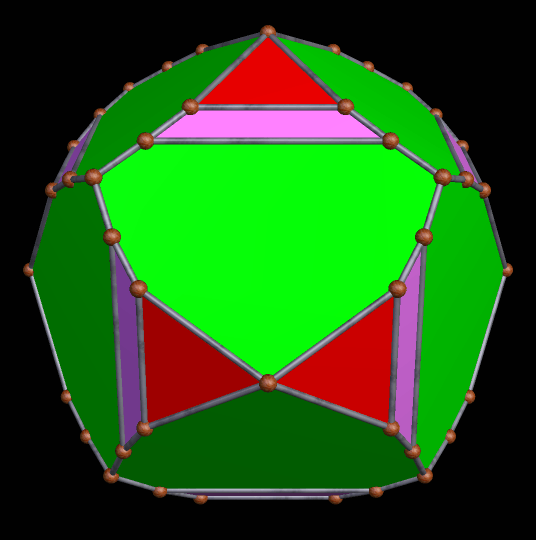
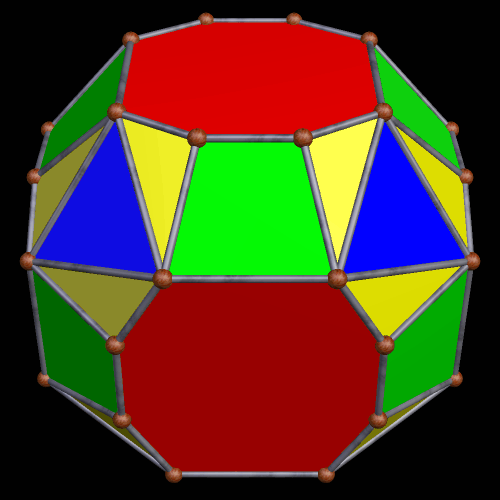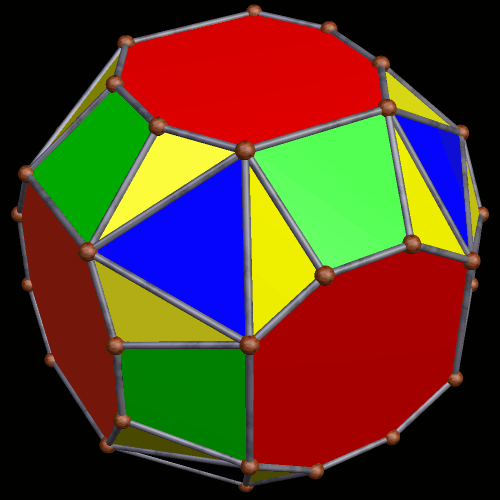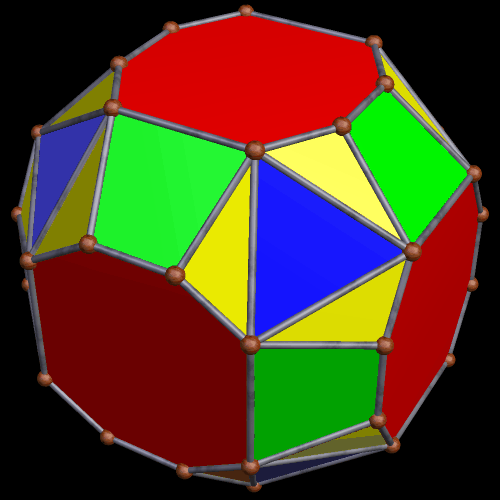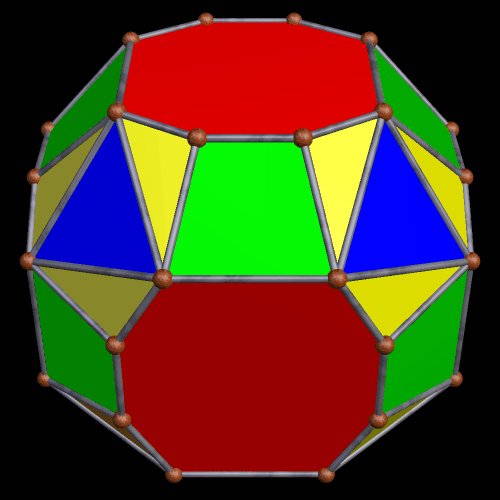
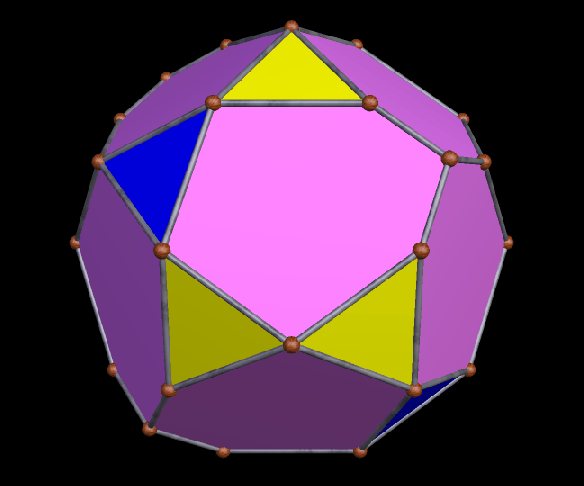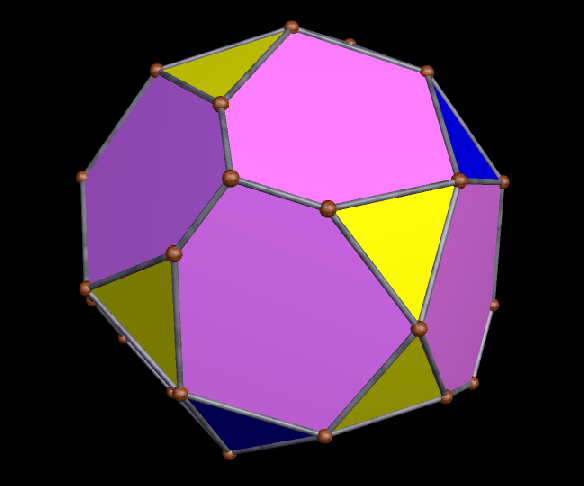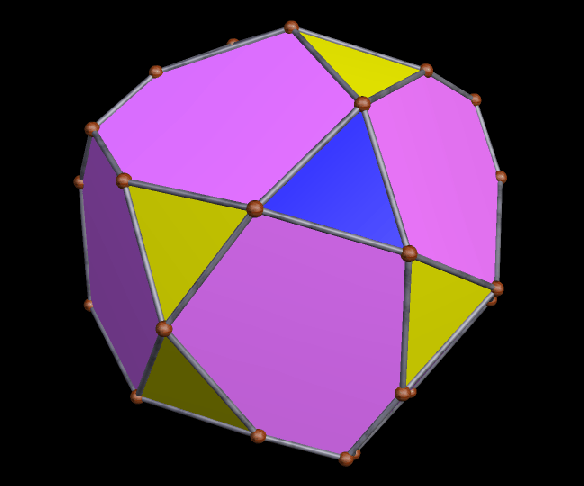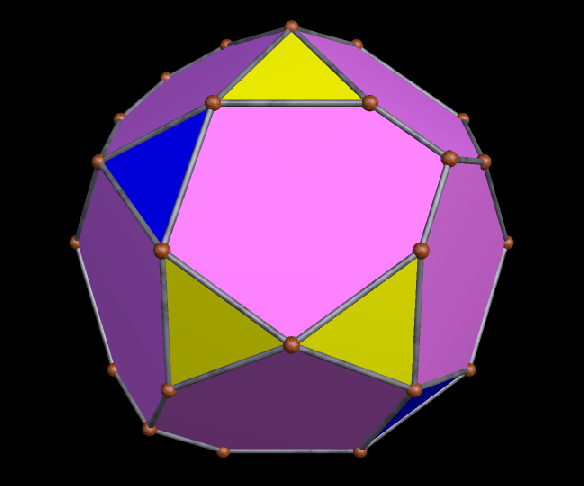
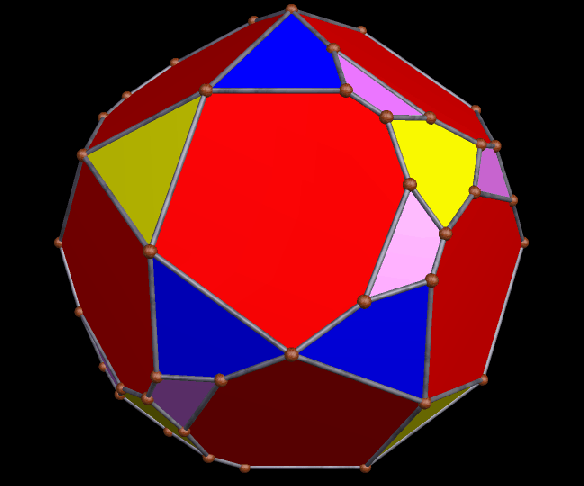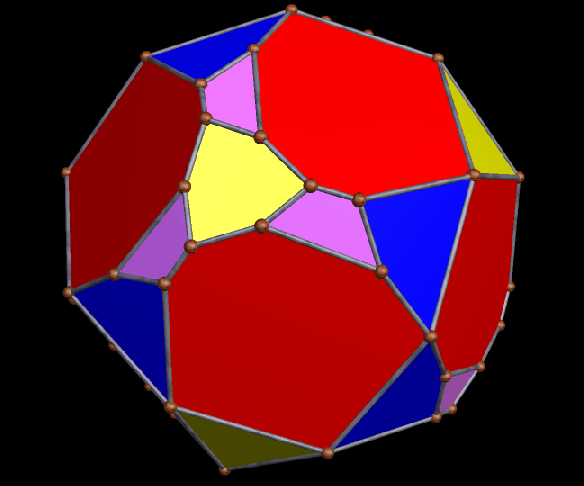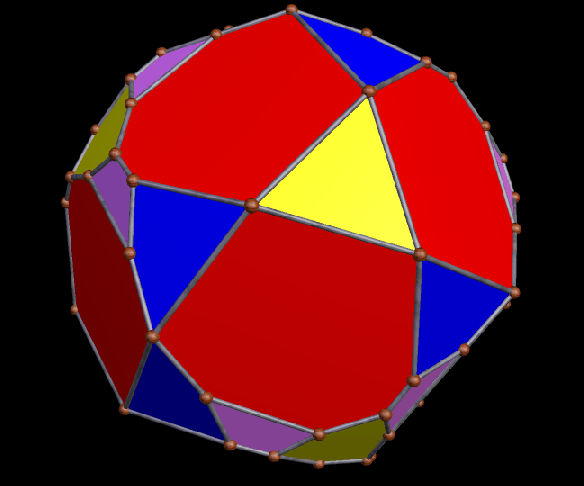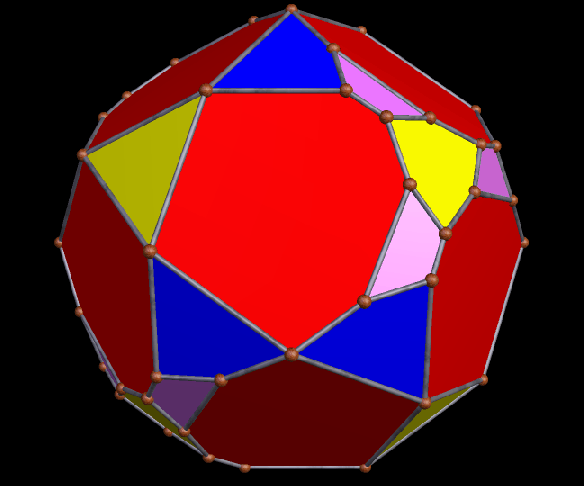
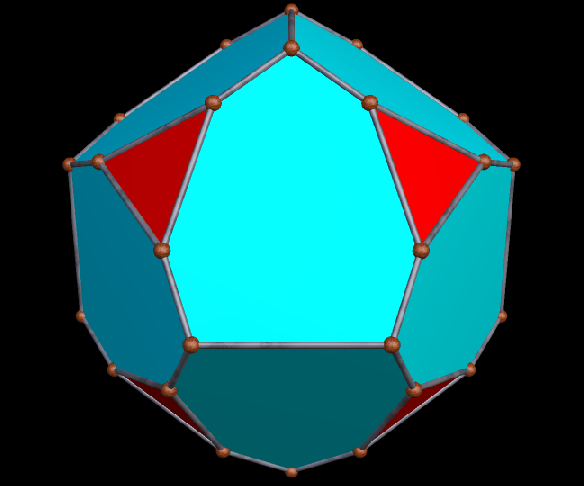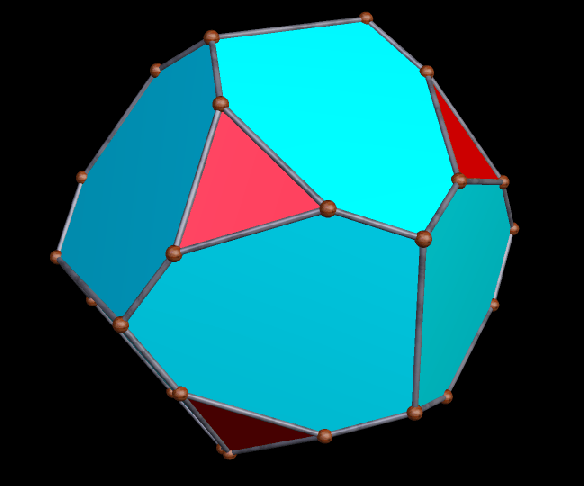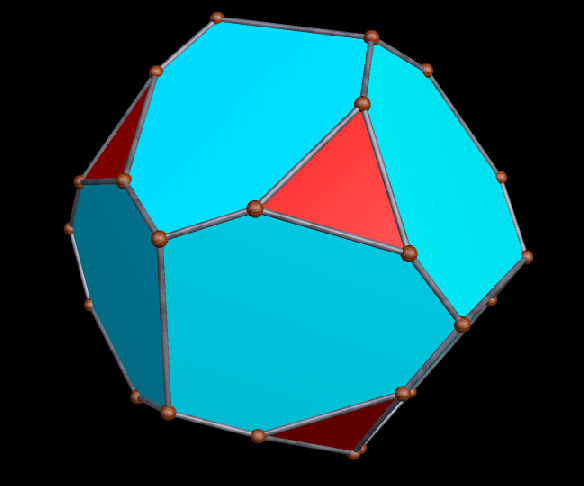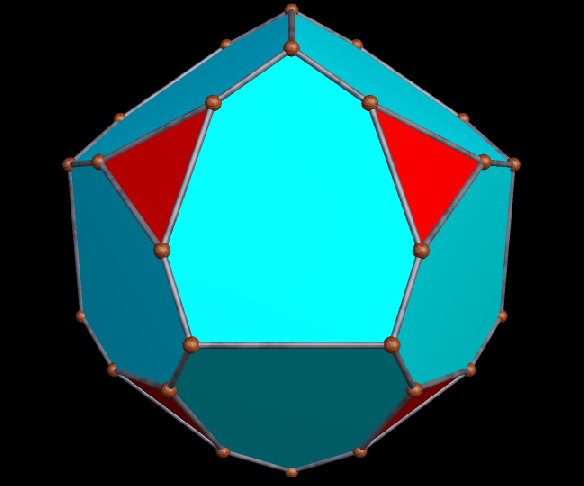
A Large Collection of Polyhedra with Pyritohedral Symmetry, Some of Them Chiral
It’s quite an informal way to define it, but pyritohedral symmetry is the symmetry-type of a standard volleyball. These images of pyritohedral polyhedra were made using Stella 4d, software available at http://software3d.com/Stella.php.
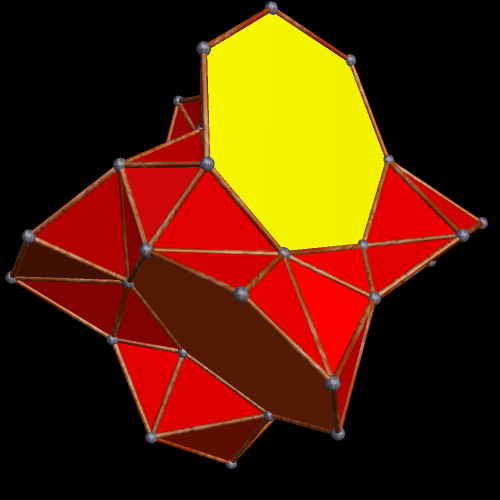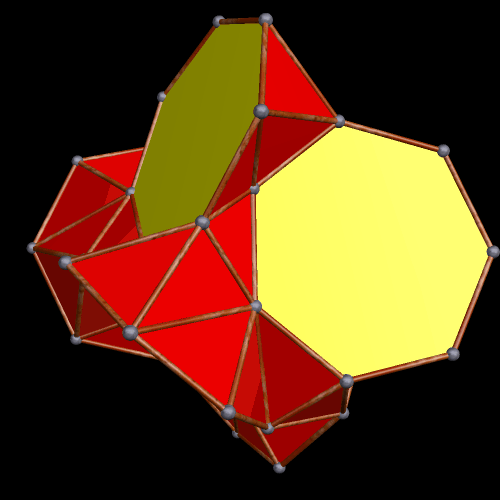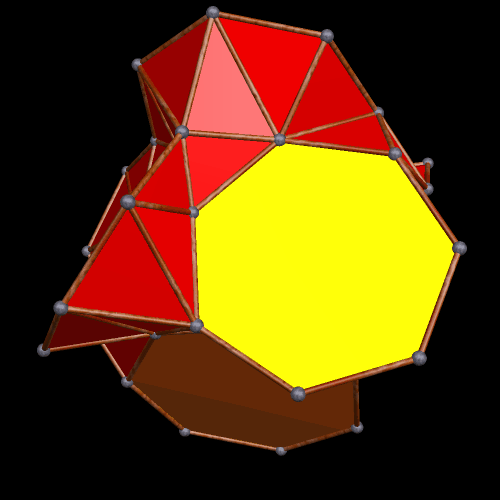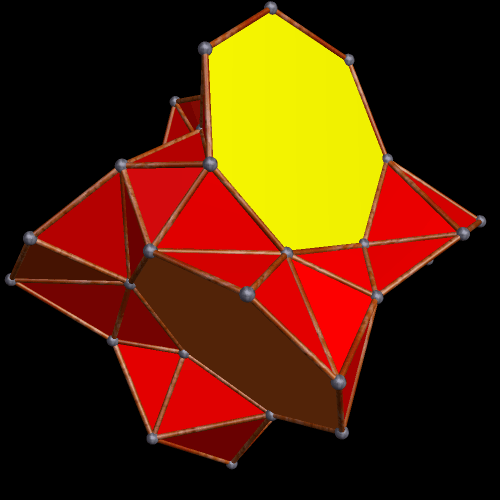
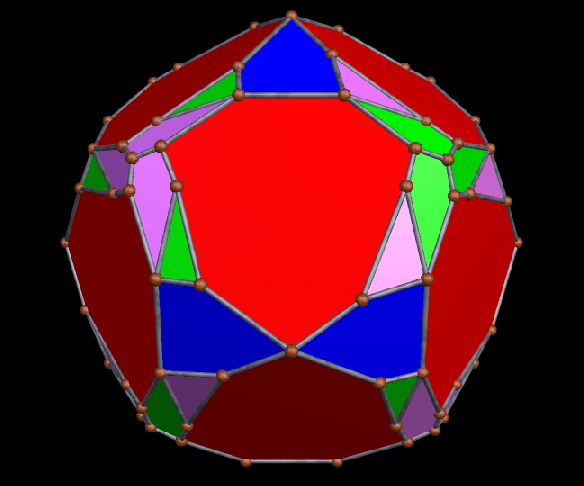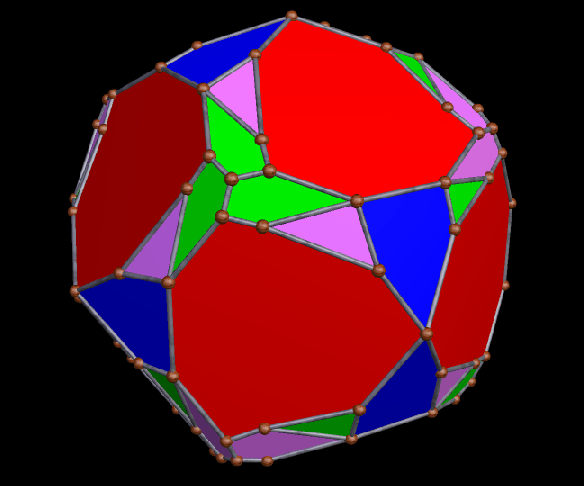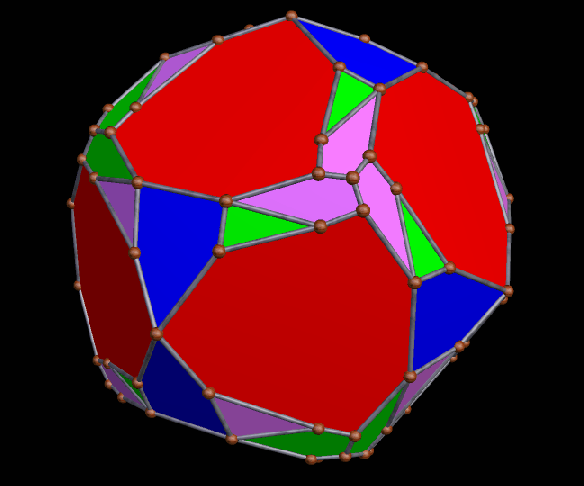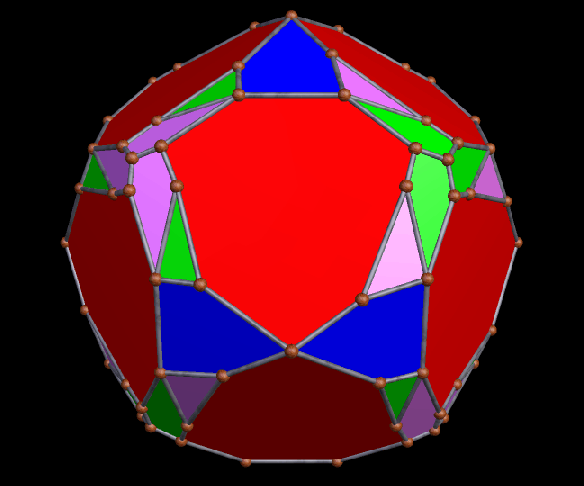
The Small Ditrigonal Icosidodecahedron, Together with Its Fifth Stellation
I made the polyhedron above by performing a faceting of the dodecahedron, and only realized, after the fact, that I had stumbled upon one of the uniform polyhedra, a set of polyhedra I have not yet studied extensively. It is called the small ditrigonal icosidodecahedron, and its faces are twelve star pentagons and twenty equilateral triangles, with the triangles intersecting each other. Below is its fifth stellation, which appears to be a compound of a yellow dodecahedron and a red polyhedron which I do not (yet) recognize, although it does look quite familiar.
Both images were created using Stella 4d, software you can try right here.
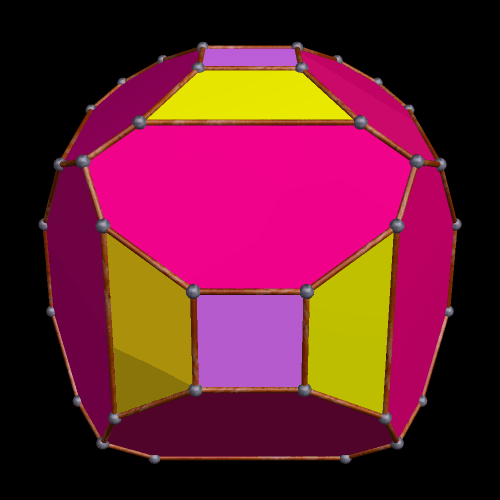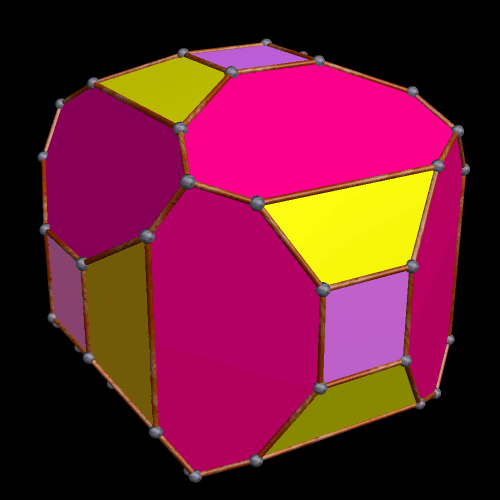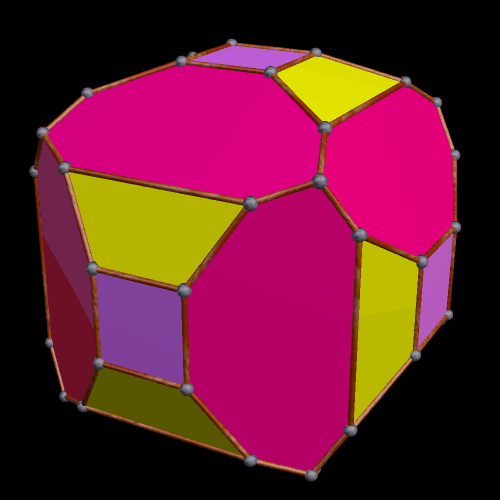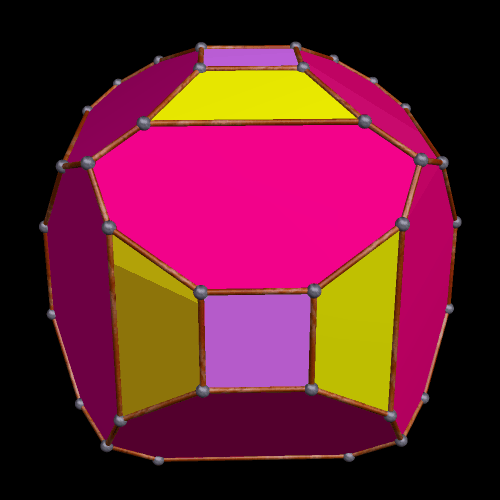
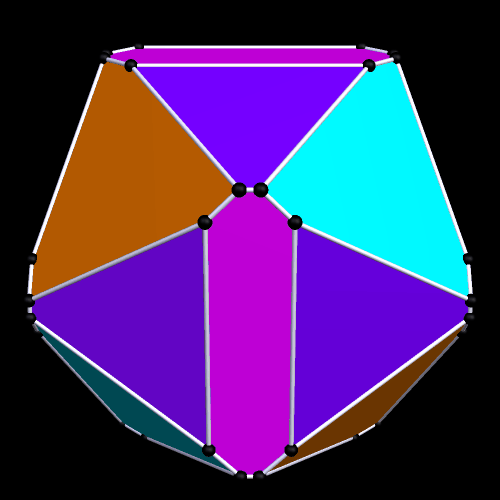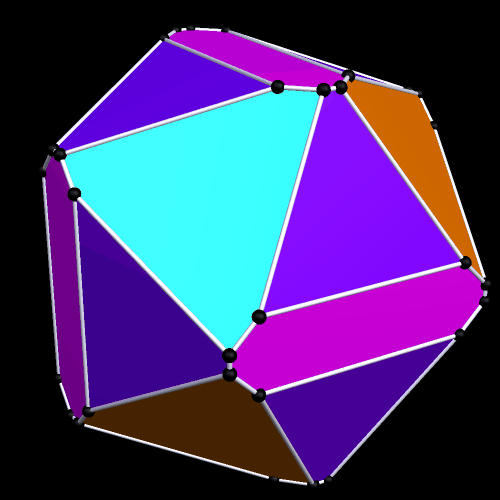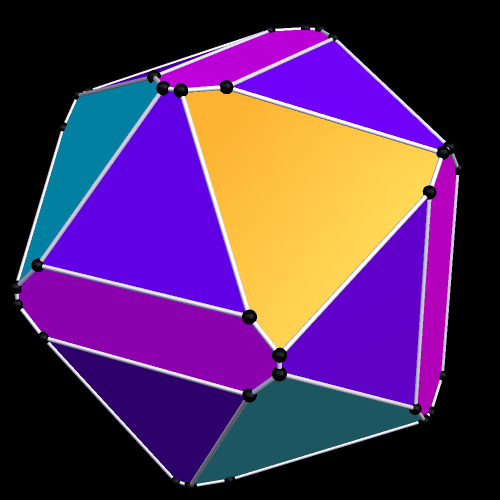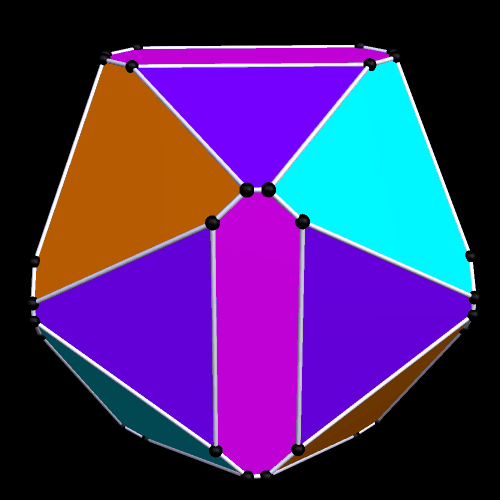
Partially Truncated Platonic and Rhombic Dodecahedra
Each of these dodecahedra were modified by truncations at exactly four of their three-valent vertices. As a result, each has four equilateral triangles as faces. In the one above, the Platonic dodecahedron’s pentagonal faces are modified into a dozen irregular hexagons by these truncations, while, in the one below, the rhombic dodecahedron’s faces are modified into twelve irregular pentagons.
Both of these polyhedra were created using Stella 4d, software you can try for yourself at this website.
A Mandala Made of Hexagons, Enneagons, and Dodecagons
Six Random Starsplosions of Non-Convex Polyhedra with Cuboctahedral Symmetry
All of these were made using Stella 4d, a program you can try for free at http://www.software3d.com/Stella.php.
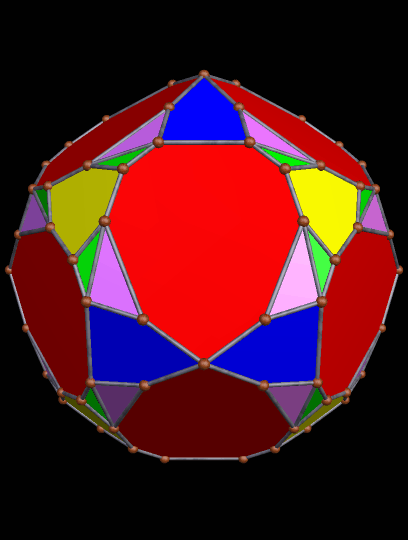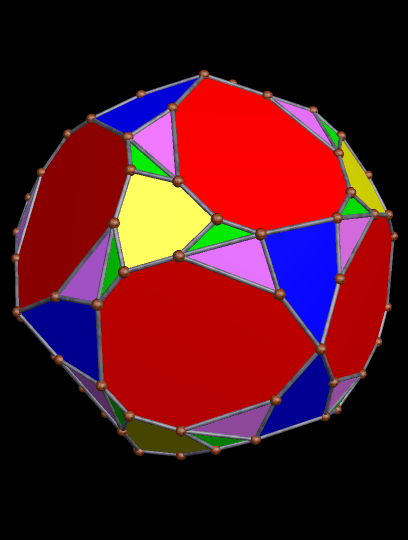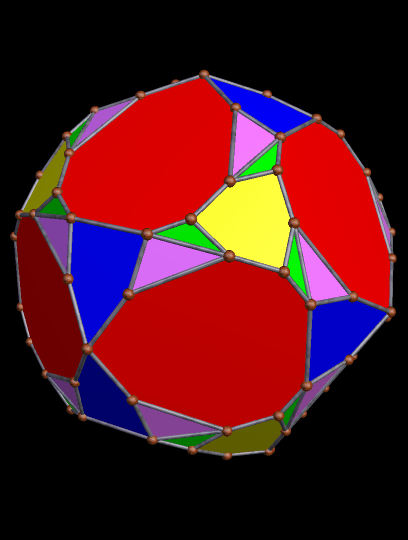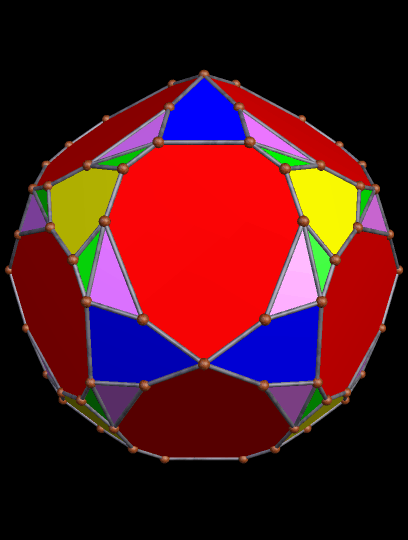
The 21st and 22nd Stellations of the Truncated Dodecahedron
Stellation of a polyhedron involves extending its faces and/or edges into space to form other polyhedra, often with a star-like appearance, which is where the words “stellation,” “stellate,” and “stellated” originate. (“Stella” is Latin for “star.”)
Since this can be done repeatedly, long stellation-series exist for many polyhedra. In the case of the truncated dodecahedron, it was the 21st and 22nd stellations which I found the most aesthetically pleasing.
Here is the 21st stellation of this polyhedron:
And here is the 22nd:
Both of these polyhedra were created with Stella 4d, software you may try for yourself, right here.
A Zonohedron with 3540 Faces, Together with Its Dual
Zonohedra are polyhedra made completely of faces which are zonogons. A zonogon is a polygon which:
- Has an even number of sides,
- Has opposite sides congruent, and
- Has opposite sides parallel.
Parallelograms are the simplest zonogons.
Here is the dual of the zonohedron above; it has 3542 faces. Although zonohedra-duals do have distinctive appearances, they do not, as a class, have a name of their own, to the best of my knowledge. They are definitely not zonohedra, themselves.
Both of these polyhedra were created with Stella 4d, software you may try for yourself, right here.
One of Many Possible Facetings of the Rhombic Triacontahedron
The simplest way I can explain faceting is that it takes a familiar polyhedron’s vertices, and then connects them in unusual ways, so that you obtain different edges and faces. If you take the convex hull of a faceted polyhedron, it returns you to the original polyhedron.
This was created using Stella 4d, software available (including as a free trial download) right here: http://www.software3d.com/Stella.php.