Tag Archives: rhombic

A Rhombic Triacontahedron, Vertices Surrounded By Smaller Rhombic Triacontahedra, and Its Interesting Dual

Posted on by
4

The first image shows a central yellow rhombic triacontahedron, with smaller, blue rhombic triacontahedra attached to each of its thirty-two vertices. The second polyhedron shown is the dual of the first one, with colors chosen by the number of sides per face in the second image — pentagons red, and triangles yellow. The convex hull of this second polyhedral complex shown would be an icosidodecahedron, itself the dual of the rhombic triacontahedron.

I use software called Stella 4d: Polyhedron Navigator to make the rotating polyhedral images on this blog. You can try Stella for yourself, for free, at http://www.software3d.com/Stella.php.

The Rhombic Octagonoid, a Zonohedron With Ninety Faces

Posted on by
9

To make this zonohedron with Stella 4d (available as a free trial download here), start with a dodecahedron, and then perform a zonohedrification based on both faces and vertices. It is similar to the rhombic enneacontahedron, with thirty equilateral octagons replacing the thirty narrow rhombic faces of that polyhedron.

I’ve run into this polyhedron from time to time, and have also had students make it. It is the largest zonohedron which can be built using only red and yellow Zome (available here) of a single strut-length (short, medium, or long). I thought it needed a name, so I made one up.

Two Images of a Toroidal Rhombic Triacontahedron Made of 212 Dodecahedra

Posted on by
4

I made these using Stella 4d, a program you can try as a free trial download at http://www.software3d.com/Stella.php.

Two Rhombic Polyhedra with Tessellated Faces

Posted on by
1

These polyhedra are the rhombic dodecahedron (above), and the rhombic triacontahedron (below).

I made both of these using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php. The tessellation on the faces of these polyhedra first appeared right here on this blog, in the post just before this one.

The Golden Rhombus, the Rhombic Triacontahedron, and the Rhombic Hexecontahedron

Posted on by
Reply

There’s a special rhombus which is called the “golden rhombus,” because its diagonals are in the golden ratio. To construct it with compass and straight edge, you first construct a golden rectangle (shown with blue edges and a yellow interior), and then connect the midpoints of its sides to form a rhombus (with edges shown in red).

Several polyhedra can be made which use golden rhombi as their faces. The most well-known of these polyhedra is the rhombic triacontahedron, which has 30 such faces. It is the dual of the icosidodecahedron.

If the rhombic triacontahedron is stellated 26 times, the result is the (non-convex) rhombic hexecontahedron. It has 60 golden rhombi as faces.

Both of these polyhedra can be constructed with Zometools (available at http://www.zometool.com). With white Zomeballs and red Zomestruts, these polyhedra look a lot like this:

The flat image at the top of this post was created using Geometer’s Sketchpad and MS-Paint. The four rotating polyhedral images were created using Stella 4d: Polyhedron Navigator, which you can purchase, or try for free, at http://www.software3d.com/Stella.php.

Partially Truncated Platonic and Rhombic Dodecahedra

Posted on by
Reply

chiral polyhedron featuring a dozen hexagons and four triangles

Each of these dodecahedra were modified by truncations  at exactly four of their three-valent vertices. As a result, each has four equilateral triangles as faces. In the one above, the Platonic dodecahedron’s pentagonal faces are modified into a dozen irregular hexagons by these truncations, while, in the one below, the rhombic dodecahedron’s faces are modified into twelve irregular pentagons.

dozen pents 4 triangles

Both of these polyhedra were created using Stella 4d, software you can try for yourself at this website.

A Rhombic Ring of Icosahedra, Leading to a Rhombic Dodecahedron Made of Icosahedra

Posted on by
4

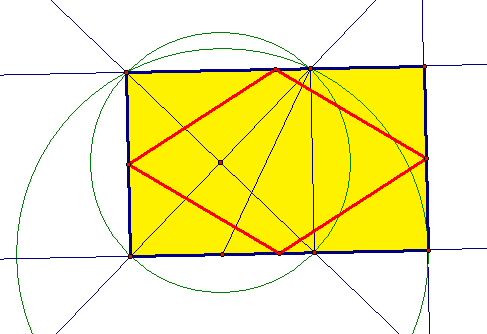
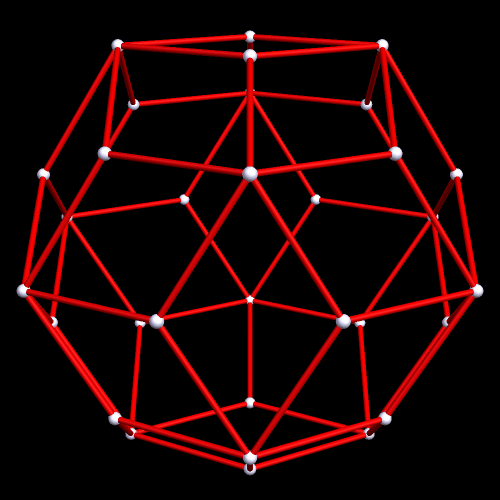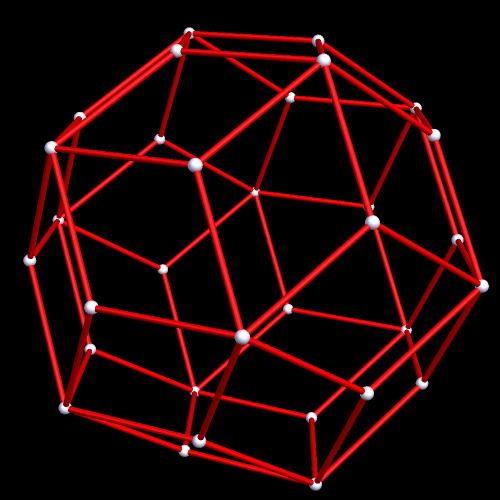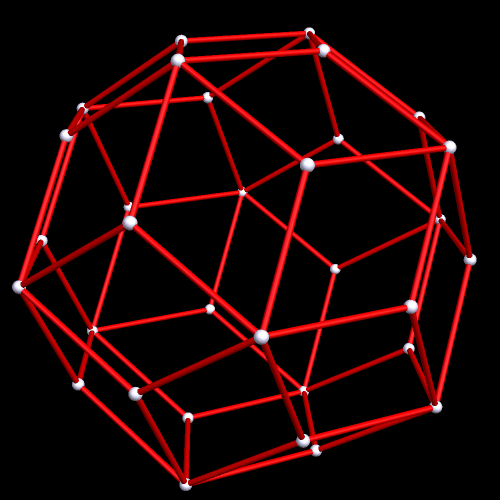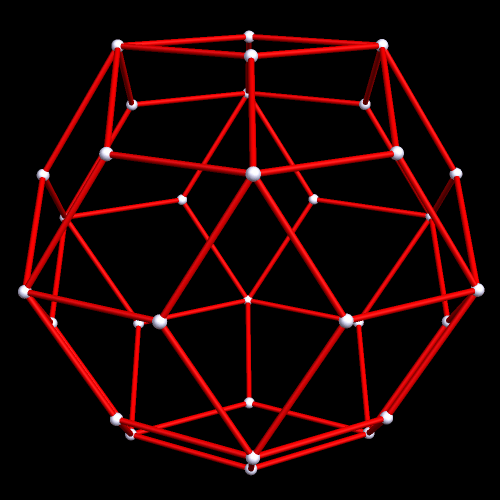
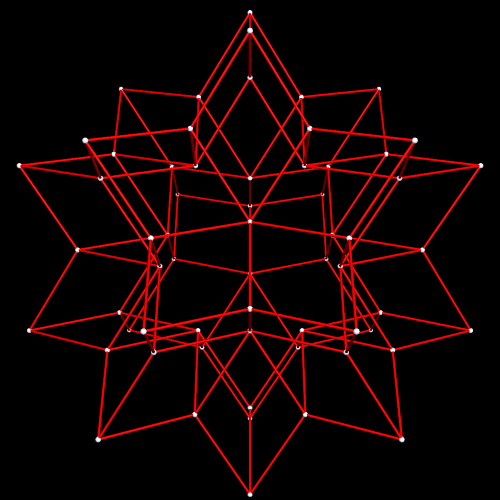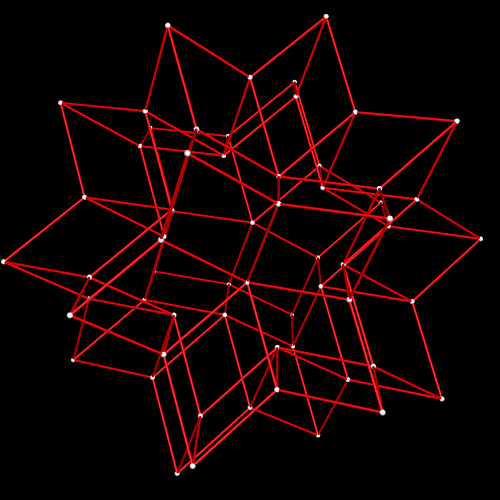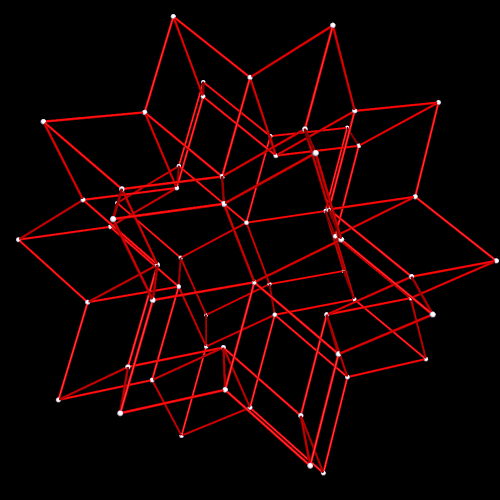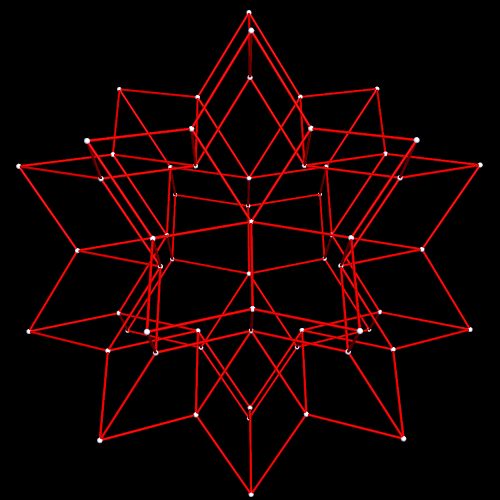
As it turns out, eight icosahedra form this rhombic ring, by augmentation:

Rhombic ring of Icosa

Measured from the centers of these icosahedra, the long and short diagonal of this rhombus are in a (√2):1 ratio. How do I know this? Because that’s the only rhombus which can made this polyhedron, a rhombic dodecahedron, dual to the cuboctahedron.

RD of Augmented Icosa

This rhombic dodecahedral cluster of icosahedra could be extended to fill space, since the rhombic dodecahedron itself has this property, an unusual property for polyhedra. Whether space-filling or not, the number of icosahedron per rhombic-dodecahedron edge could be increased to 5, 7, 9, or any greater odd number. Why would even numbers not work? This is a consequence of the fact that opposite faces of an icosahedron are inverted, relative to each other; a pair of icosahedra (or more than one pair, producing odd numbers > 1 when added to the vertex-icosahedron) must be attached to the one at a rhombic-dodecahedron-vertex to make these two inversions bring the triangular face back around to its original orientation, via an even number of half-rotations, without which this consruction of these icosahedral rhombi cannot happen.

Here’s another view of this rhombic dodecahedron, in “rainbow color” mode:

RD of Augmented Icosa RB

All images above were produced using Stella 4d, software which may be tried for free right here.