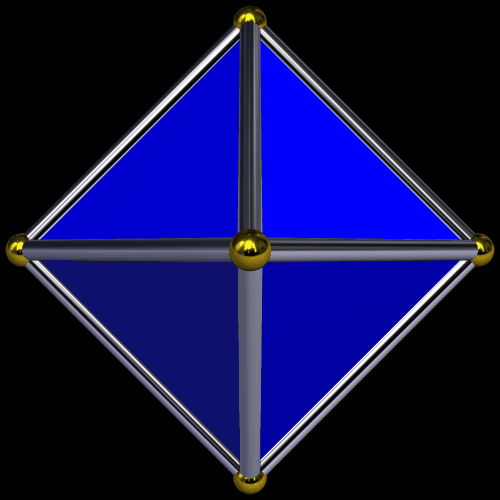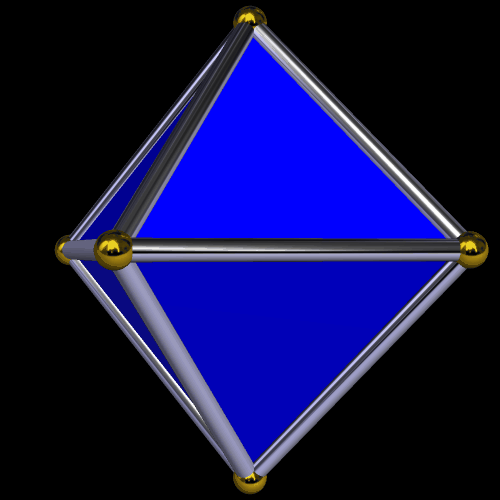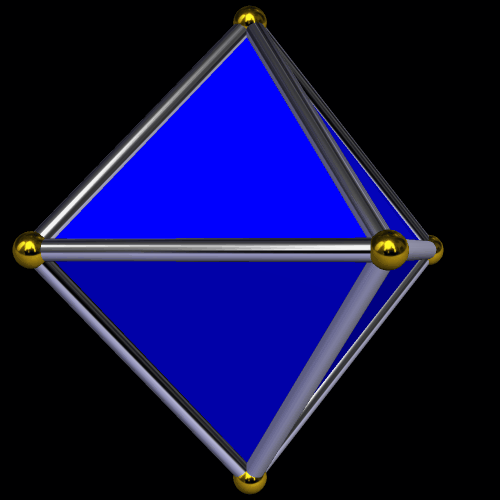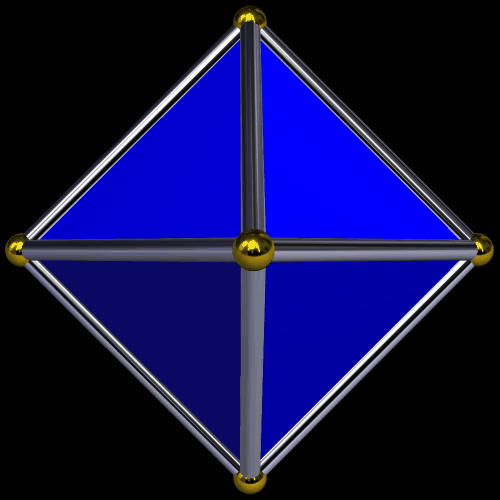
Start with points A and B. Construct a circle, centered on A, with radius AB. Draw line AB, which intersects this circle at B and C. Construct a second line which is perpendicular to the first line, intersecting it at A. Let the two intersections of the circle and this second be named points D and E.

Bisect segment AB, and call its midpoint F. Construct a line containing D and F. If the circle’s radius is two, then AF = FB = 1, while AD = 2. By the Pythagorean Theorem applied to right triangle DAF, then, DF = sqrt(5). Construct a second circle centered on F, with radius DF. Construct point G where this circle intersects segment AC. It follows that FG, being another radius of this second circle, has a length of sqrt(5). This makes BG = FB + FG = 1 + sqrt(5).

Construct the line which is perpendicular to line AE and passes through point E. Next, construct the two lines perpendicular to line AB and passing through points G and B. These two lines intersect the first line described in this paragraph at two points: H (below G) and I (below B). ABIE is a square with edge length two, and both GBIH and AEHG are golden rectangles.