Creating a Faceting of the Truncated Icosahedron

Posted on 13 January 2015 by RobertLovesPi

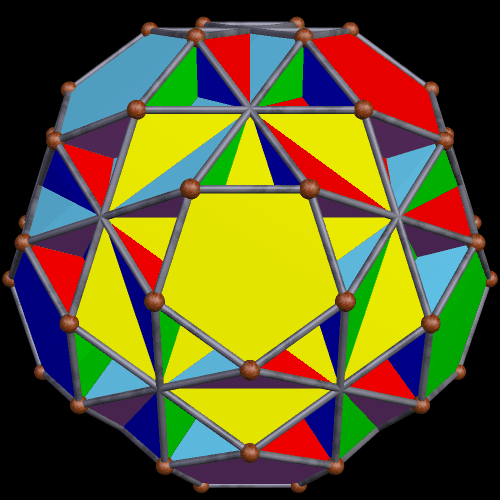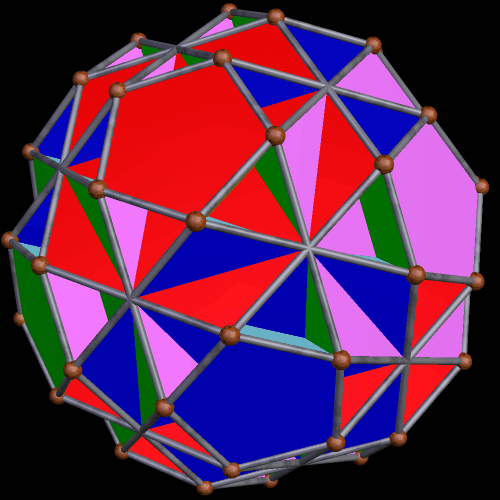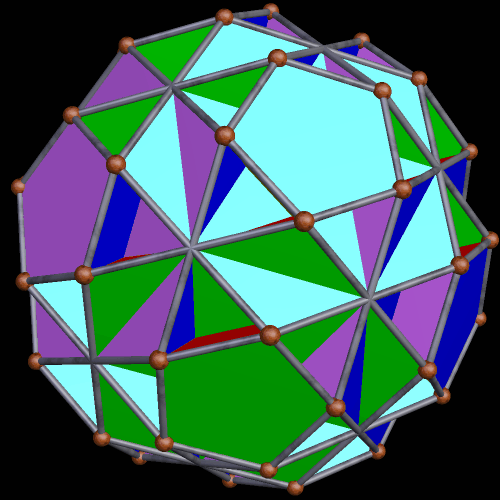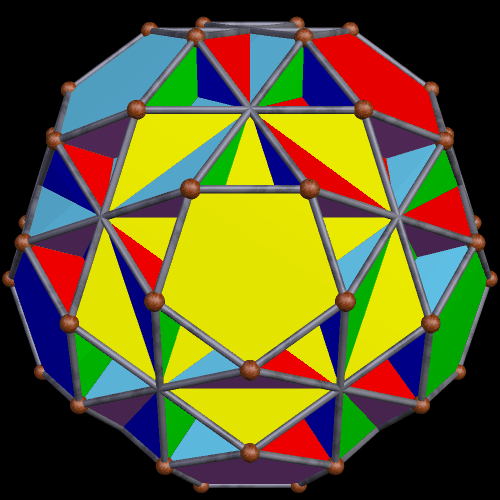
To make a faceted polyhedron, vertices of the original polyhedron are connected in new ways, to create a different set of faces and edges. To make this particular faceting of the truncated icosahedron, I first connected all vertices in the configuration shown below, to make irregular decagonal faces in the interior of the solid.

In this next pic, the decagonal faces formed above are shown in red, and a new set of pentagonal faces is being created.

For a polyhedron to be considered mathematically valid, faces must meet in pairs at each edge. To accomplish that, I had to create another set of pentagonal faces, this one smaller than the last, as shown below.

Here’s the completed polyhedron, with each face-type having its own color.

This next image is of the same polyhedron, but with a different coloring-scheme. In this second version, each face has its own color — except for faces which are parallel, with those faces given the fame color.

I created these images using Stella 4d: Polyhedron Navigator, a program which is available here.

A Faceting of the Snub Dodecahedron

Posted on 6 August 2014 by RobertLovesPi

The snub dodecahedron is chiral, meaning it appears in left- and right-handed forms. This faceted version, where the same set of vertices is connected in different ways (compared to the original), possesses the same property.

Chiral polyhedra can always be tranformed into interesting polyhedral compounds by combining them with their own mirror-images. If this is done with the polyhedron above, you get this result, presented with a different coloring-scheme.

Both of these images were created using Stella 4d: Polyhedron Navigator, and you may try it at www.software3d.com/Stella.php.

One of Many Possible Facetings of the Rhombicosidodecahedron

Posted on 4 August 2014 by RobertLovesPi

I created this using Stella 4d: Polyhedron Navigator, available at www.software3d.com/Stella.php. Faceting involves connecting different sets of vertices (relative to the original polyhedron) to form new edges and faces. The new edges and faces, both, typically intersect each other, although often not as many times as in this particular example of a faceted polyhedron.