A Red Great Icosahedron, Backed With More Red

Posted on 13 February 2025 by RobertLovesPi

I made this using Stella 4d, which you can try for free at this website.

A Blue-On-Blue Rendering of the Final Stellation of the Icosahedron

Posted on 5 February 2025 by RobertLovesPi

I made this using Stella 4d: Polyhedron Navigator, which you can try for free at http://www.software3d.com/Stella.php.

The Great Rhombicosidodecahedron, Adorned With Images From the Saturnian System

Posted on 18 January 2025 by RobertLovesPi

In this rotating image of a great rhombicosidodecahedron, the decagonal faces show images of Saturn and its rings. The hexagons show Saturn’s largest moon, Titan. The moon Mimas, with its giant crater that makes it resemble the “Death Star,” from Star Wars, is shown on the square faces. These either are, or are close to, the true colors of these astronomical images. Titan appears to have little or no detail because of its thick, hazy atmosphere. Also, these three images are not shown to scale.

I found these images using Google-searches, and the only one that requires personal credit is the photograph of Titan, which was taken by Kevin M. Gill. Also, I assembled them onto this polyhedron, and created the rotating .gif above, using Stella 4d, a program you can try for free at http://www.software3d.com/Stella.php.

Tessellation of the Plane with Regular Hexagons, Squares, and Tetraconcave, Equilateral Octagons, #2

Image

If you’d like to see the first version of this tessellation, made over a decade ago, this is where you’ll find it. https://robertlovespi.net/2014/06/08/tessellation-of-the-plane-with-regular-hexagons-squares-and-tetraconcave-equilateral-octagons/

A Tessellation Made of Many Circles

Image

Hexagonal Tessellation of Semicircles

Image

Two Symmetrohedra Which Each Feature Four Regular Enneagons

Posted on 6 January 2025 by RobertLovesPi

This symmetrohedron has the following faces: four regular enneagons, four equilateral triangles, and twelve isosceles triangles with vertex angles of 43.5686 degrees. Its net is shown below.

If this polyhedron is stellated once, the result is another symmetrohedron — one with four enneagonal faces, as well as twelve kites. The angles in the kites are 116.762, 99.8348, 43.5686, and 99.8348 degrees, and their side lengths are in a 1:2.2946 ratio.

Finally, here is a net for this kite-and-enneagon solid.

I used Stella 4d: Polyhedron Navigator to make everything you see here. If you’d like to try this software for yourself, a free trial download is available at http://www.software3d.com/Stella.php.

A Polyhedral Journey, Starting With the Truncated Tetrahedron

Posted on 5 January 2025 by RobertLovesPi

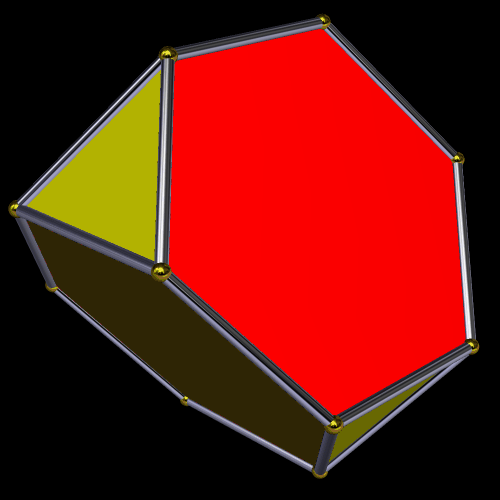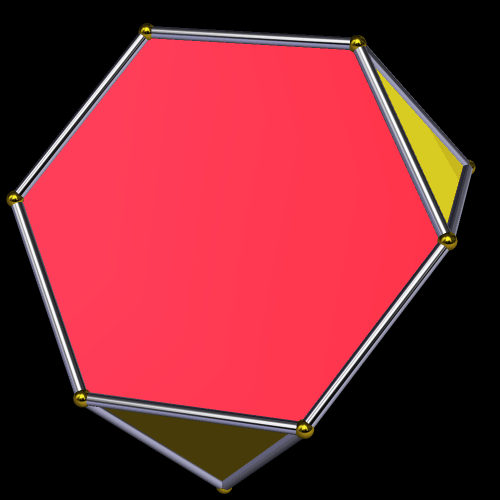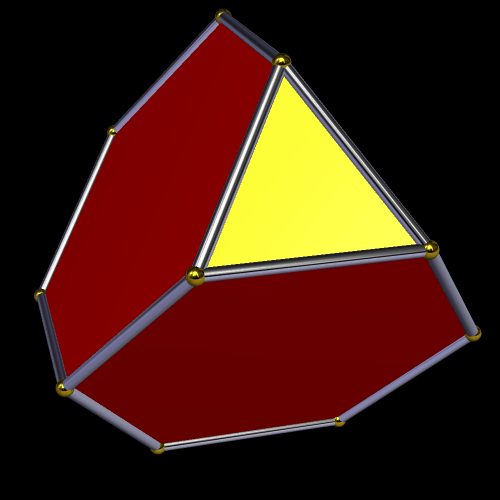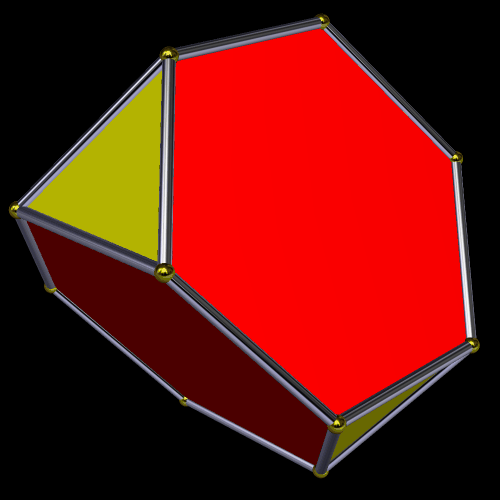
Here’s the truncated tetrahedron. It is the simplest of the Archimedean solids.

I decided to “take a walk” with this polyhedron. First, I used Stella 4d (available here) to make the compound of this solid and its dual, the Catalan solid named the triakis tetrahedron.

Next, also using Stella (as I’m doing throughout this polyhedral journey), I formed the convex hull of this polyhedron — a solid made of kites and rhombi.

For the next polyehdron on this journey, I formed the dual of this convex hull. This solid is a symmetrohedron, featuring four regular hexagons, four equillateral triangles, and twelve isosceles triangles.

Next, I used a function of this program called “try to make faces regular.” Some this function works, and sometimes it doesn’t, if it isn’t mathematically possible — as it the case here, where the only thing that remained regular was the equilateral triangles. The hexagons in the resulting solid are equilateral, but not equiangular.

The next thing I did was to examine the dual of this latest polyhedron — another solid made of kites and rhombi, but with broader rhombi and narrower kites.

I then started stellating this solid. The 16th stellation was interesting, so I made a virtual model of it.

Stellating this twice more formed the 18th stellation, which turned out to be a compound of the cube and a “squished” version of the rhombic dodecahedron. This is when I decided that this particular polyhedral journey had come to an end.