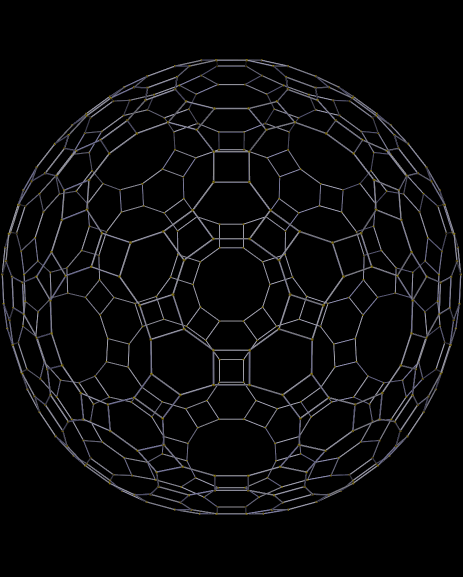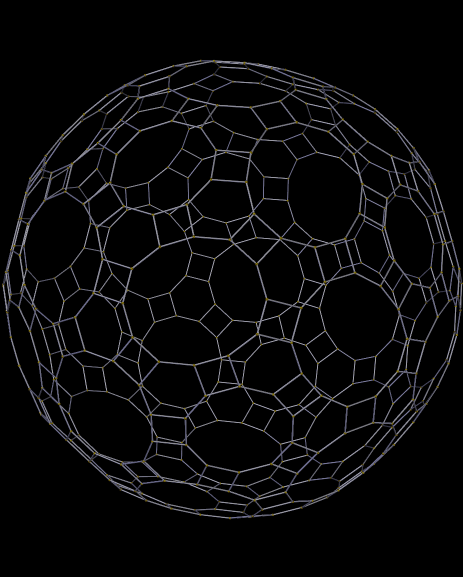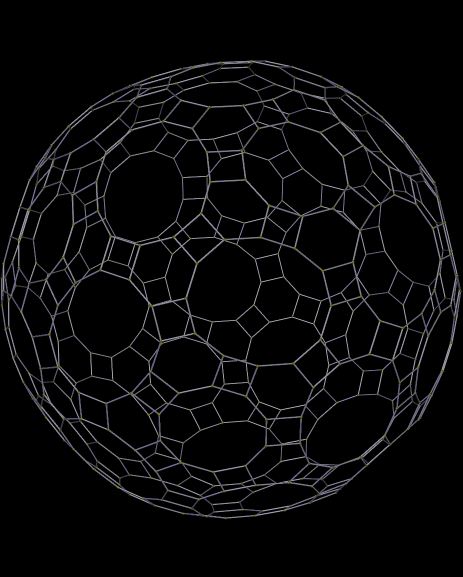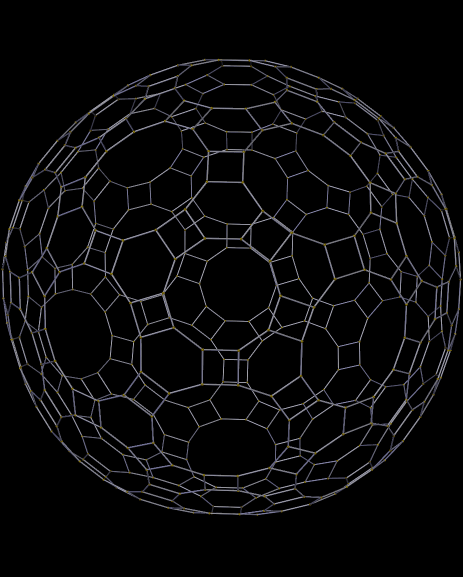
Little blurbs about posts on this blog get auto-tweeted on my Twitter, @RobertLovesPi. There’s also an A.I. on Twitter, @Hexagonbot, who retweeted my last two tweets about blog-posts here, but will not be retweeting the tweet about this one.
Why is this? Simple: @Hexagonbot is programmed to retweet any tweet which contains the word “hexagon,” which was in the titles of the last two posts here (also tessellations). This tessellation has no hexagons, though, and so the @Hexagonbot will not find it worthy of attention.
I cannot explain why hexagons get their own bot on Twitter, but other polygons do not have such bots. It’s simply one of the mysteries of the Internet.