Some Variants of Kepler’s Stella Octangula

Posted on 20 September 2014 by RobertLovesPi

The Stella Octangula is also known as the compound of two tetrahedra, which works well because the tetrahedron is self-dual. All of these are also two-part compounds, with varying amounts of similarity to the Stella Octangula. The first one is also the 26th stellation of the triakis octahedron, one of the Catalan solids.

All of these were made using Stella 4d, which may be tried or purchased at http://www.software3d.com/Stella.php.

Two Compounds of Six Tetrahedra Each

Posted on 19 September 2014 by RobertLovesPi

In the image above, which I stumbled upon using Stella 4d (available here), the tetrahedra are elongated. If they are regular, instead, the same arrangement looks very different:

Selections from the Stellation-Series of the Strombic Icositetrahedron, Including Some Polyhedral Compounds

Posted on 18 September 2014 by RobertLovesPi

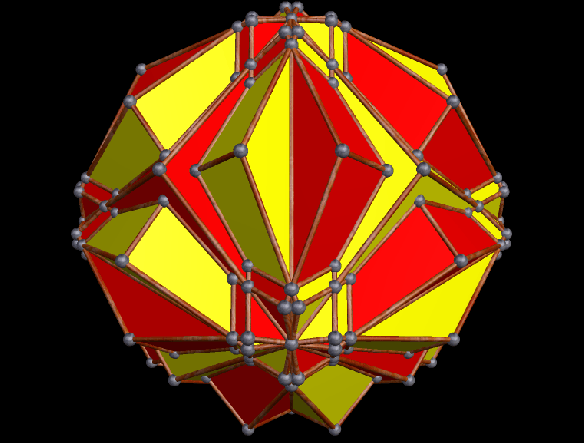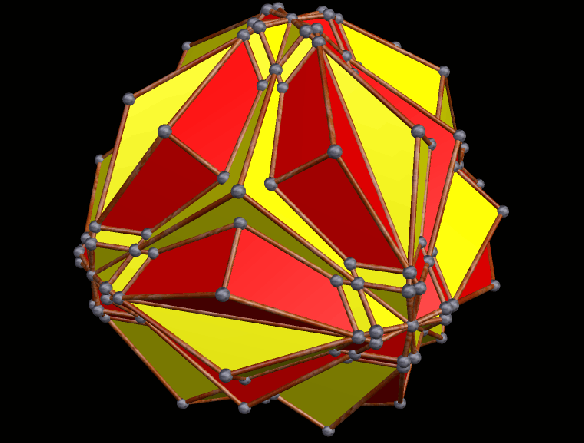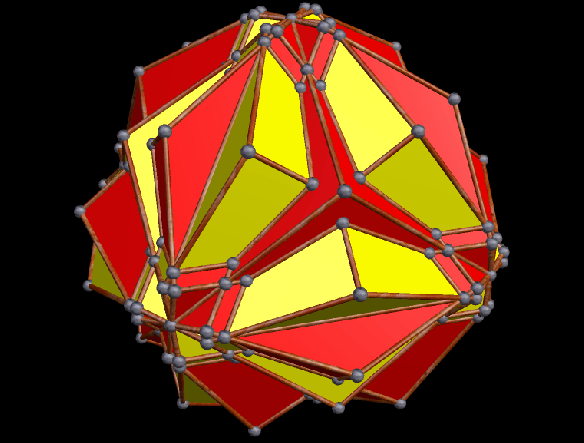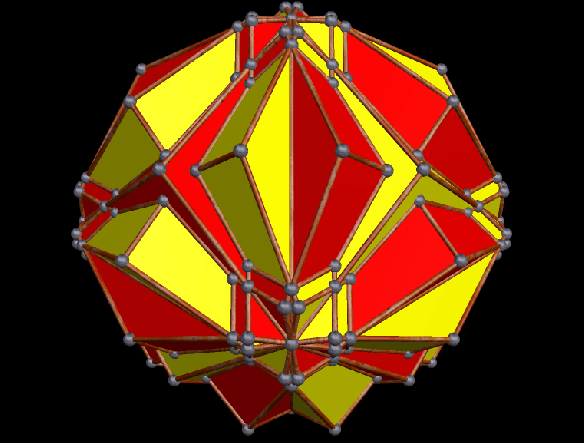
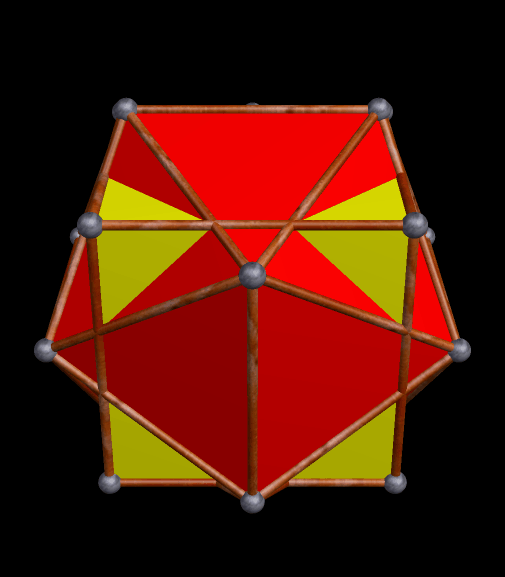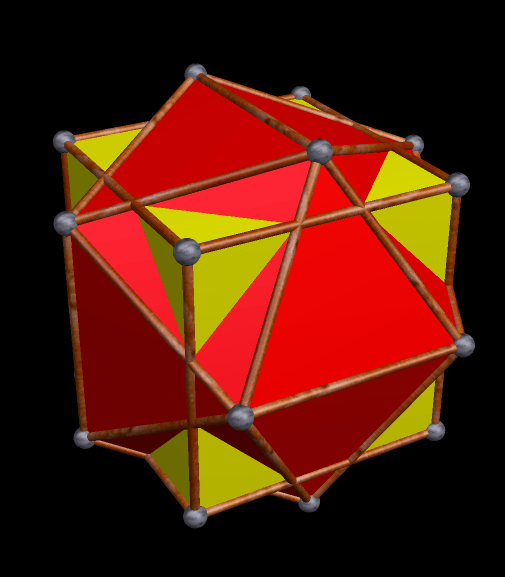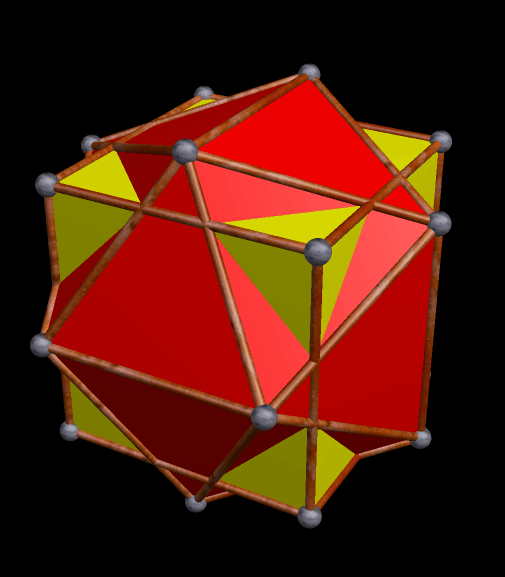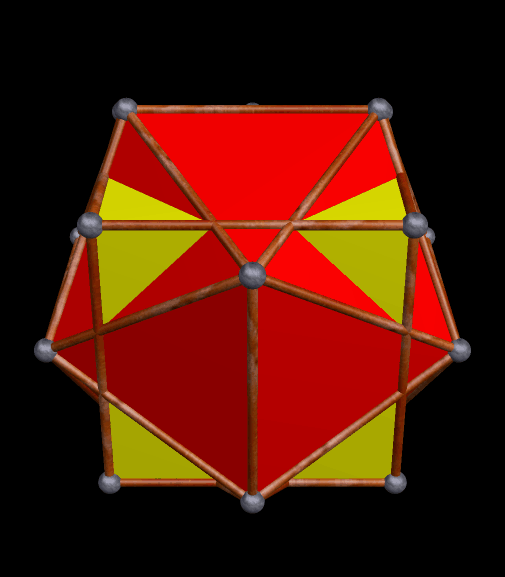
The strombic icositetrahedron is the dual of the rhombcuboctahedron, and has many interesting polyhedra in its stellation-series. Here are a few of them, starting with the 10th stellation.

Here’s the strombic icositetrahedron’s 16th stellation:

And the 19th:

And the 21st:

And the 23rd:

And the 25th:

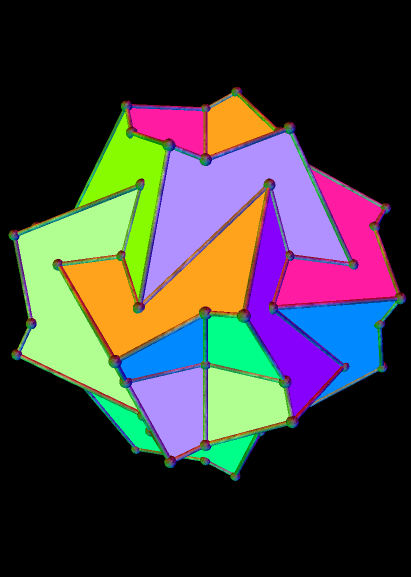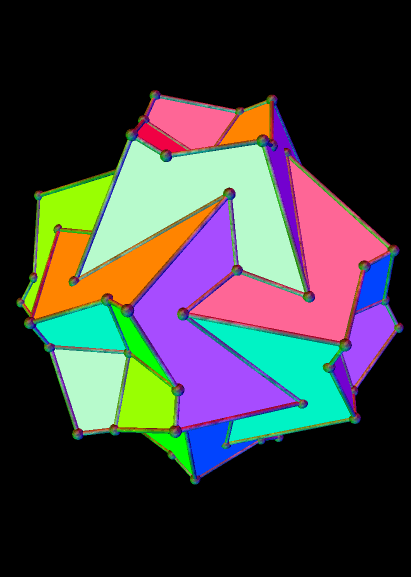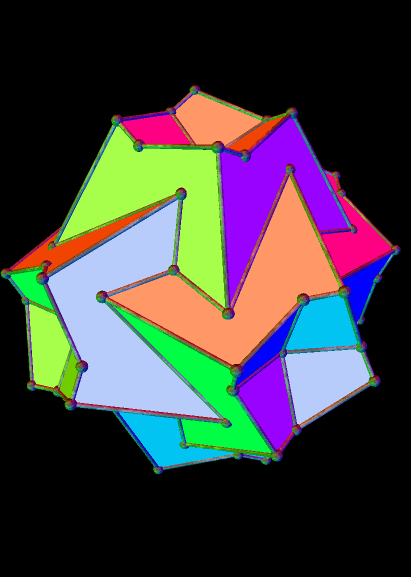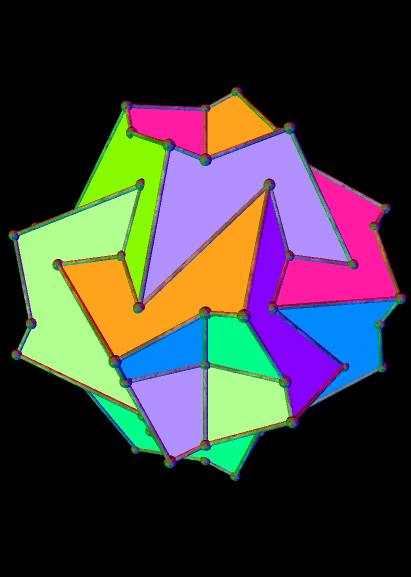
And the 26th:

Next, the 28th stellation. It isn’t colored as the other stellations above are colored, simply because it is also a compound of six off-center square-based pyramids.

The 34th stellation is even more interesting. It’s a symmetrical four-part compound, but the component polyhedra have irregular faces, and are much less symmetrical than the compound itself.

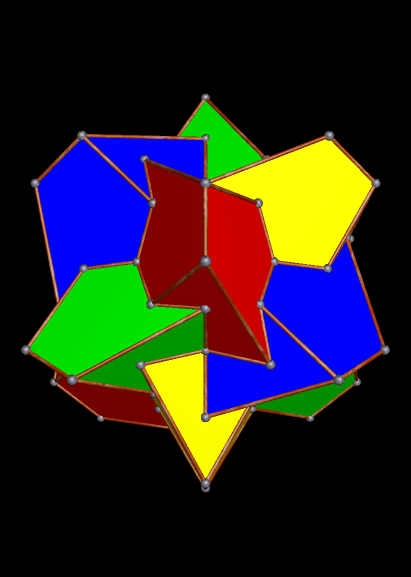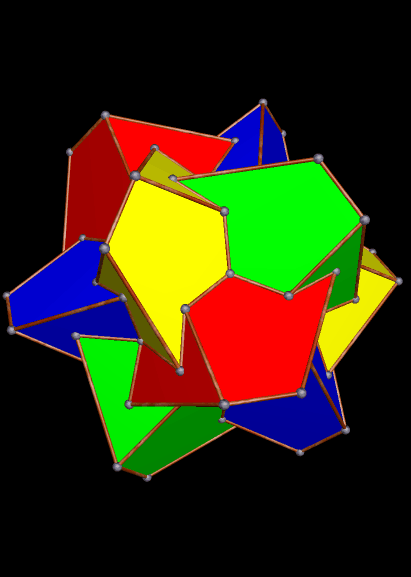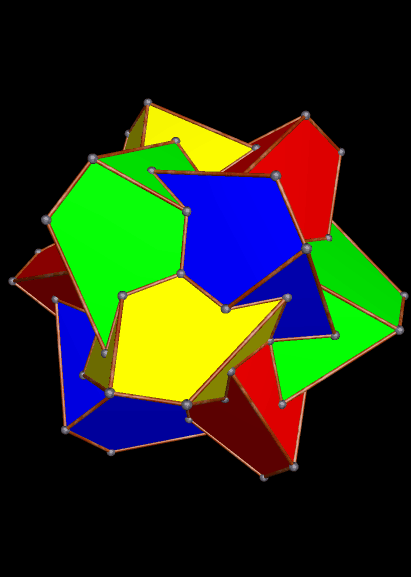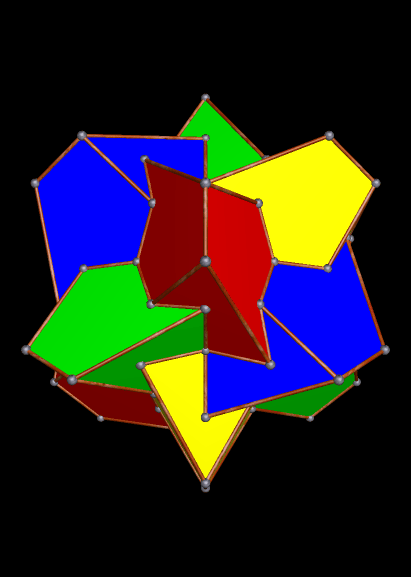
Here is the 37th stellation in this series:

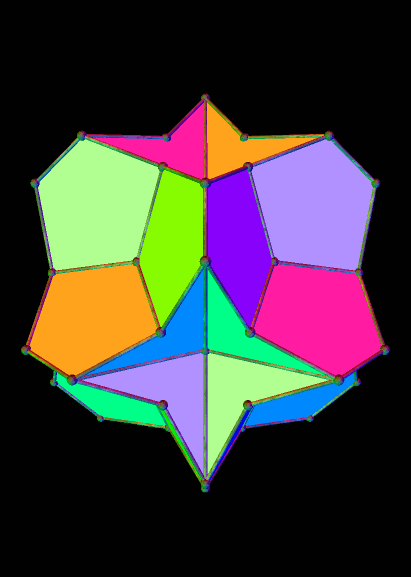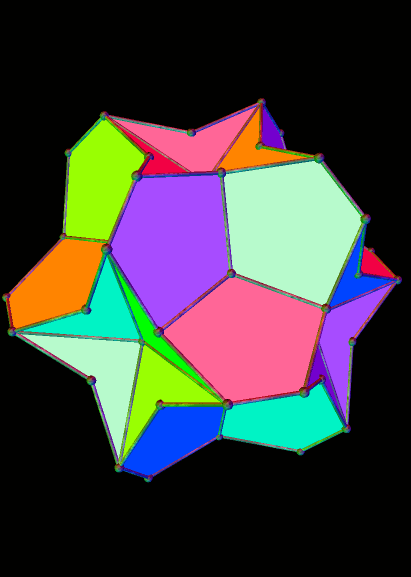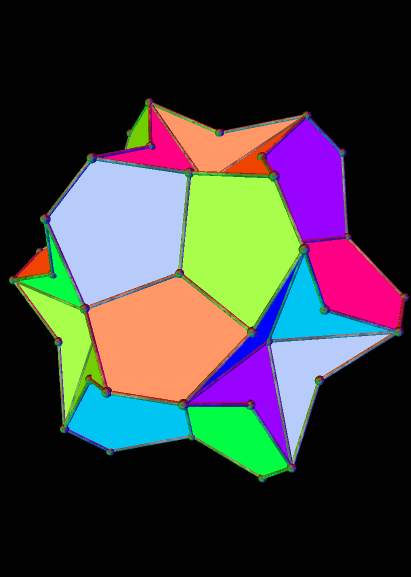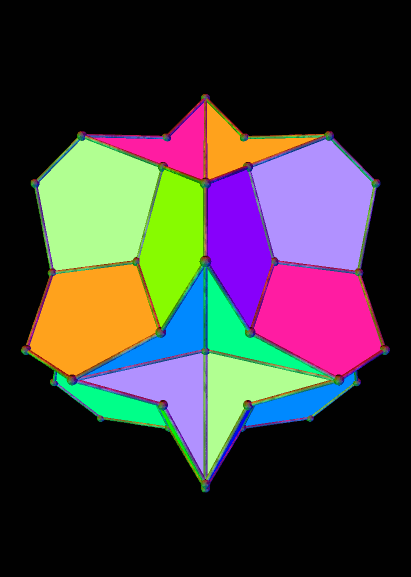
And the 43rd:

And the 44th:

The 59th stellation in this series is an octahedron, with each face excavated by short, triangle-based pyramids. It can also be seen as a compound of three shortened square-based dipyramids, but coloring it as a compound proved difficult, so it is presented here in rainbow-color mode:

Here’s the 61st stellation:

And the 68th:

And the 71st:

And the (quite different from the 71st) 72nd stellation:

And the 73rd:

And, finally, the 74th, which is an interesting two-part compound.

And the 79th:

And the 82nd stellation:

The last one I’m showing here is the 93rd stellation, another four-part compound.

All these images were created using Stella 4d: Polyhedron Navigator, which you may try for yourself at http://www.software3d.com/Stella.php.

Compound of Three Eight-Faced Trapezohedra

Posted on 18 September 2014 by RobertLovesPi

I made this using Stella 4d, which you can try right here. In addition to being a compound of trapezohedra, it is also the sixth stellation of the triakis octahedron, the dual of the truncated cube.

Four-Part Compound of Thin Parallelopipeds

Posted on 17 September 2014 by RobertLovesPi

I made this using Stella 4d: Polyhedron Navigator. You may try this program for free at http://www.software3d.com/Stella.php.

More Polyhedra, Including Some Compounds, from the Stellation-Series of the Tetrakis Cube

Posted on 16 September 2014 by RobertLovesPi

The next one is a compound of eight off-center pyramids. By this point, I had gone so far into the stellation-series (a search I began when preparing the post before this one) that I had lost count.

This one is a compound of three short square-based dipyramids:

This one, according to Stella 4d, is a compound of three parts, but I can’t quite figure out what the parts are!

Here is another “mystery compound,” this one with two parts:

Stella 4d, which I used to make these, may be tried here.

Two Compounds of Dipyramids from the Stellation-Series of the Tetrakis Cube

Posted on 16 September 2014 by RobertLovesPi

The 16th stellation of the tetrakis cube, the dual of the truncated octahedron, is a compound of three elongated octahedra, or square dipyramids:

The 65th stellation of this same polyhedron is of another compound of dipyramids, but these are triangular dipyramids with obtuse faces, and there are four of them:

I generated both of these images with Stella 4d: Polyhedron Navigator, available right here.

How to Get Fair Dice with Various Numbers of Possible Results, from Two to Thirty, Using Different Polyhedra

Posted on 13 September 2014 by RobertLovesPi

For a d2, number a cube’s faces with three ones and three twos.
For a d3, number a cube’s faces 1,1,2,2,3,3.
The standard d4 is a Platonic solid, the tetrahedron. Double-numbered (two ones, two twos, etc.) octahedra are sometimes used as d4s, also.
For a d5, an icosahedron can be renumbered with four each of the numbers one through 5. Double-numbering a pentagonal dipyramid or pentagonal trapezohedron also works.
The d6 is the familiar cube.
For a d7, one option is to roll an octahedron, but re-roll 8 each time it comes up.
For a d9, one option is to roll a d10, but reroll 10s.
For d10s, pentagonal dipyramids and pentagonal trapezohedra both work. There is also the option of double-numbering an icosahedron.
For a d11, one option is to roll a d12, but reroll 12s.
For a d12, the Platonic and rhombic dodecahedra both work.
For a d13, roll a d14, but reroll 14s.
For a d14, one option is to roll a d7 and a d2, then add 7 to the d7 result iff the d2 shows 2. Another is to roll a d15, but reroll 15s.
For a d15, simply double-number the thirty faces of a rhombic triacontahedron.
For a d16, roll a d2 and a d8 together, using the d8 result, but adding 8 to the d8 result iff the d2 result is 2.
For d17, roll a d18, but reroll 18s.
For d18, roll a d2 and a d9 together, using the d9 result, but adding 9 to the d9 result iff the d2 result is 2.
For d19, roll a d20, but reroll 19s.
For d20, icosahedra are used.
For d21, one option is to roll a d24, rerolling any result from 22-24. Another is roll a d7 and a d3 together, using the d7 result, but adding 7 to this d7 result iff the d3 result is 2, but adding 14 to the d7 result iff the d3 result is 3.
For d22, one option is to roll a d24, rerolling any 22s and 24s. Another is to roll a d2 and a d11 together, using the d11 result, but adding 11 to this d11 result iff the d2 result is 2.
For d23, use a d24, and re-roll 24s.
Options for the d24 include the triakis octahedron, the tetrakis cube, the deltoidal icositetrahedron, and the pentagonal icositetrahedron, all of which are Catalan solids (duals of the Archimedeans). Another d24 can be made by rolling a d2 and a d12 together, and using the d12 result, but adding 12 to this d12 result iff the d2 result is 2.
For a d25, roll two distinguishabale d5s, called d5a and d5b. The 1-25 random number is (d5a)+ (5)(d5b-1).
For a d26, roll a d13 and a d2, then add 13 to the d13 result if the d2 shows 2. Another is to roll a d15, but reroll 15s. The first option may require two different d2s, so they will have to be distinguishable, in that case, or one d2 must be rolled twice, each for a different purpose.
For a d27, roll a d9 and d3 together. The result is (d9) + (9)(d3-1).
For a d28, roll a d14 and d2 together, using the d14 result, but adding 14 to it iff the d2 result is 2. Another option: roll a d30, but reroll results of 28 or 29. The first option may require two different d2s, so they will have to be distinguishable, in that case, or one d2 must be rolled twice, each for a different purpose.
For a d29, roll a d30, and reroll 30s.
The most common d30 is a rhombic triacontahedron. After the Platonic solids and the d10, these d30s are the most commonly available example of polyhedral dice.