polyhedral | RobertLovesPi.net

By Request: The Compound of Five Rhombic Dodecahedra, with Nets

Image

By Request: The Compound of Five Rhombic Dodecahedra, with Nets

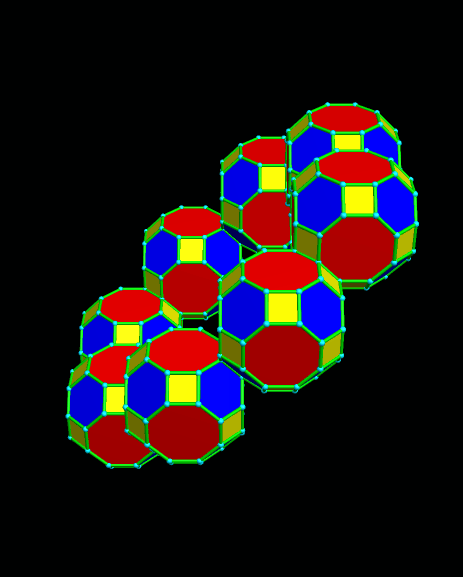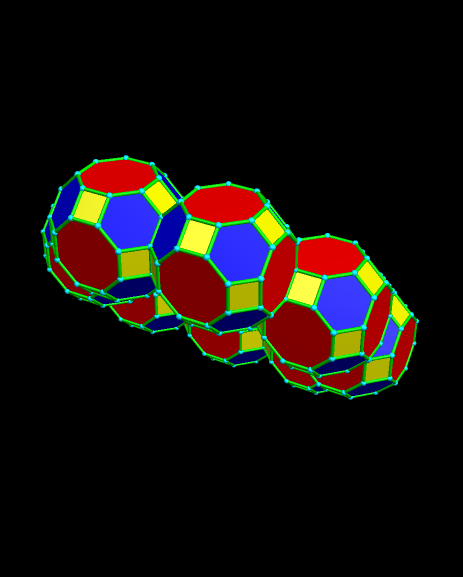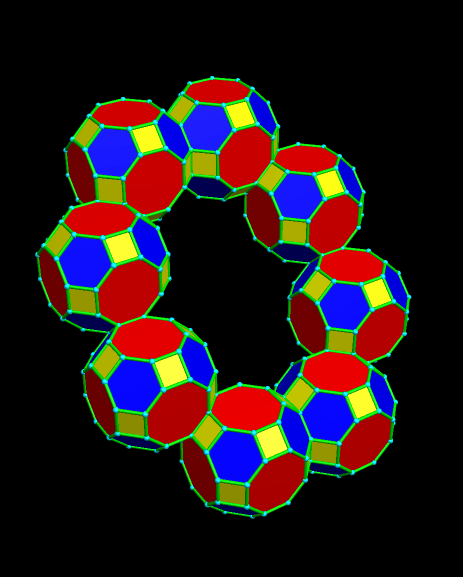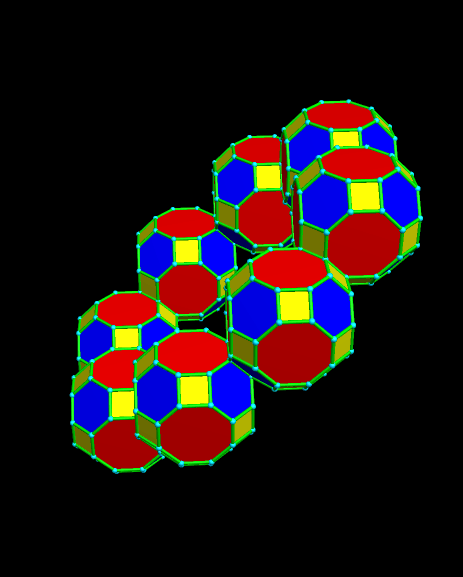
I’ve been asked by a reader of this blog to post nets for this polyhedral compound. Printing nets with Stella 4d is easy, and I’m happy to post them here, in response to that request. Warning, though: there are many nets needed for this compound.

Each of these smaller images may be enlarged with a single click.

Here’s the first net type needed (above). You’ll need thirty copies of this net. The gray parts show, and the white parts are tabs to help put it together. Below is the second type needed, of which you need sixty copies.

There’s also a third type of net, and these last two types may need to be rescaled before you print them, to fit the net of the first type, also. You’ll need sixty copies of this third net (below) as well, It’s the mirror-image of the net of the second type.

Finally, here’s a non-rotating image of the completed polyhedron, to help with the construction:

I recommend using card stock or posterboard, and trying to get as much tape as possible on the inside of the model, making an uncolored version — and then painting it with five different colors of your choice, after the model is assembled. Happy building!

[Software credit: I used Stella 4d: Polyhedron Navigator to create all these images. It’s available at http://www.software3d.com/Stella.php. Downloading and trying a trial version is free, but you have to buy the fully-functioning version to print nets, or to make these rotating .gif files I post all over this blog.]

The Great Rhombcuboctahedron As a Building-Block

Image

The Great Rhombcuboctahedron As a Building-Block

This solid, also known as the great rhombicuboctahedron, and the truncated icosidodecahedron, can be used to build many other things. In addition to the elongated ring of eight above, for example, there’s this octagonal prism.

Remember the elongated ring at the top of this post? This pic, directly above, is of a ring of four of those rings.

And, yes, that’s a (non-great) rhombcuboctahedron made of great rhombcuboctahedra. Here it is again, with a different color-scheme.

For the last of these constructions, eight more great rhombcuboctahedra are added to the figure in the two posts above, which is also returned to its original color-configuration. These eight new polyhedra have positions which correspond to the corners of a cube.

Manipulating polyhedra in this manner is easy with Stella 4d, the program I used to do all of this. You may buy it, and/or try a free trial version first, at www.software3d.com/Stella.php.

Octahedron with Beveled Vertices

Image

Octahedron with Beveled Vertices

As an eight-sided die, this would work better than the Platonic octahedron, for it would roll more smoothly.

Software credit: see http://www.software3d.com/Stella.php.

Polyhedral Quilt Pattern

Image

Polyhedral Quilt Pattern II

I made this using Stella 4d, which you may try for free at http://www.software3d.com/Stella.php.

Compound of a Slightly-Truncated Isocahedron and a Rhombic Triacontahedron

Image

Compound of a Slightly-Truncated Isocahedron and a Rhombic Triacontahedron

Software used: Stella 4d, available at http://www.software3d.com/Stella.php (including a free “try it before you buy it” trial download).

The Hextrated Pentagonal Icositetrahedron

Image

The Hextrated Pentagonal Icositetrahedron

Years ago, I split a dodecahedron into four panels of pentagons, rotated the pentagon-panels and moved them outward from the center, and did so just the right amount to create gaps that could be filled with triangles. Thus was named the tetrated dodecahedron, which you can read more about here: https://en.wikipedia.org/wiki/Tetrated_dodecahedron

The choice of word “tetrated” was somewhat unfortunate, for tetration already exists in mathematics, as a means of expressing very large numbers, and which I shall not explain here. I didn’t learn this until much later, though, and by that time, it was too late to turn “tetrate” into something else. It had come to mean an operation one does on a polyhedron: break it into four multi-face panels, move them out and rotate them just enough, and fill the resulting gaps with triangles.

As such, “tetrate” can, in the geometrical sense, be modified for differing numbers of panels of multiple faces from a polyhedron. Consider the pentagonal icositetrahedron, the dual of the snub cube. Here, it has been split into six panels, and then each panel moved out from the center and rotated, with triangles filling the gaps. The triangles differ between color-groups slightly, but are close to equilateral, except for the ones shown in green, which simply are equilateral.

(Image created with Stella 4d — software you can try yourself at http://www.software3d.com/Stella.php.)

A Variant of Kepler’s Stella Octangula

Image

A Variant of Kepler's Stella Octangula

Johannes Kepler named the compound of two tetrahedra the “stella octangula,” thus helping make it one of the best-known polyhedral compounds today. This variant uses triakis tetrahedra in place of the Platonic tetrahedra in that compound. The triakis tetrahedron is a Catalan solid, and is dual to the truncated tetrahedron.

Software credit: see http://www.software3d.com/stella.php to try or buy Stella 4d, the software I used to create this image.

The Compound of Six Dodecahedra

Image

The Compound of Six Dodecahedra

Some polyhedral compounds are well-known, such as the compound of five cubes, while others are less famous. I had never heard of this compound before building one today (virtually, not as a physical model). However, a quick Google-search told me that I was not the first person to discover it.

Software credit: see http://www.software3d.com/stella.php to try or buy Stella 4d, the software I used to create this image.

Rhombicosidodecahedral Cluster of Rhombic Triacontahedra

Image

Rhombicosidodecahedral Cluster of Rhombic Triacontahedra

Since rhombic triacontahedra can form pentagonal rings, triangular rings, and square rings, I wanted to find out if a rhombicosidodecahedron could be built out of these building blocks. As you can see here, the attempt was a success. Each rhombic triacontahedron which appears here is located at the vertex of a rhombicosidodecahedron.

Software credit: see http://www.software3d.com/stella.php.