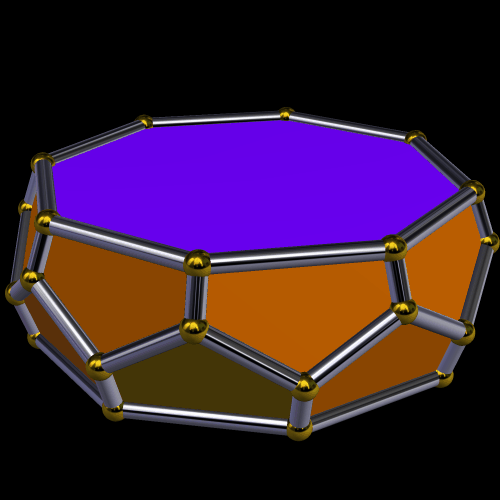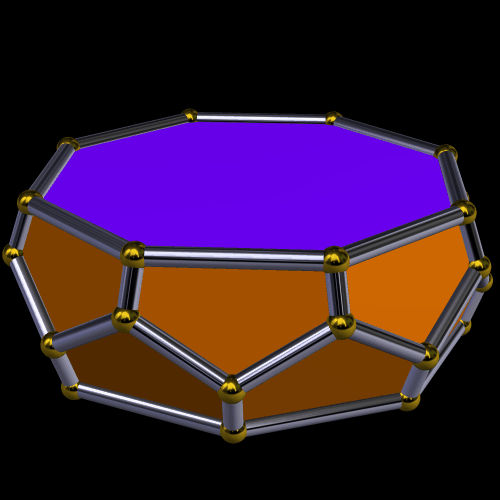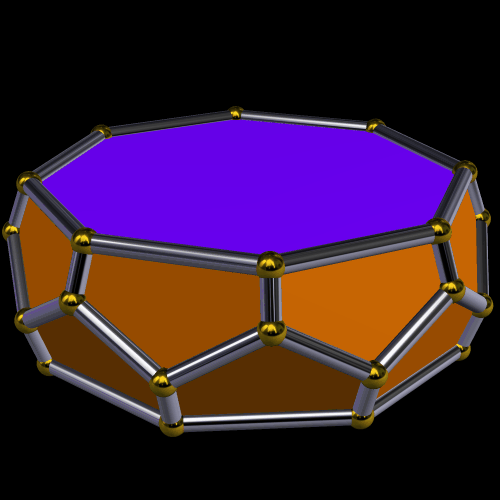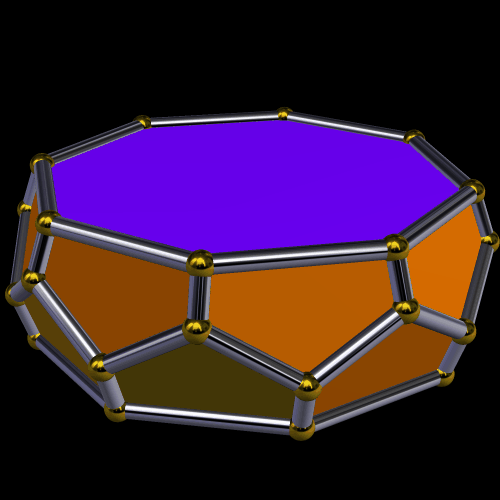
This is a zonohedrified pentagonal prism. It has ninety rhombic faces, and they are based on the vertices of that prism. I made it using Stella 4d, which you can buy, or try for free, at http://www.software3d.com/Stella.php.
Tag Archives: polyhedron
A Modified Square Antiprism with Pentagons as Lateral Faces
I made this using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.
An Enneahedron
Enneahedra are nine-faced polyhedra. This particular one has three square faces, and six kite faces. I made it from a triangular prism, using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.
A Compound of Two Square-Based Pyramids
I made this using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.
Seven Polyhedra with Eightfold Dihedral Symmetry, Starting with the Octagonal Antiprism
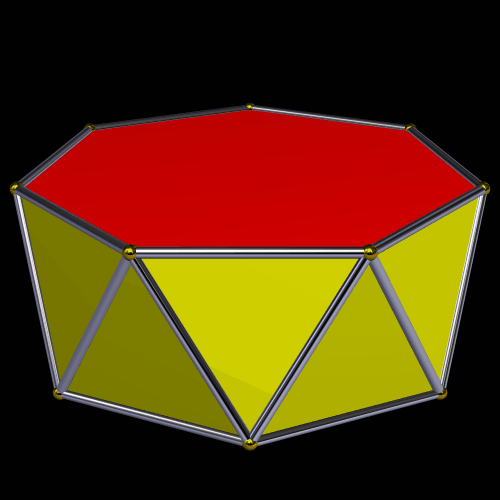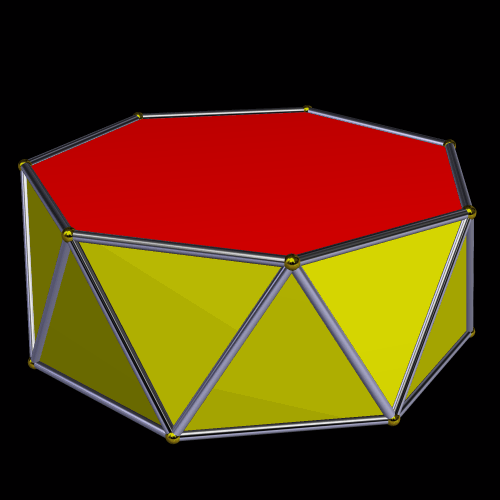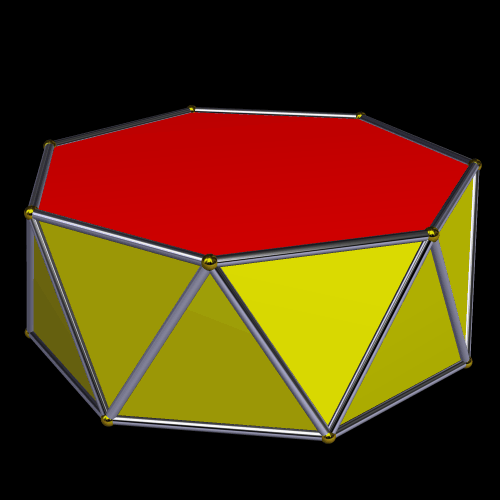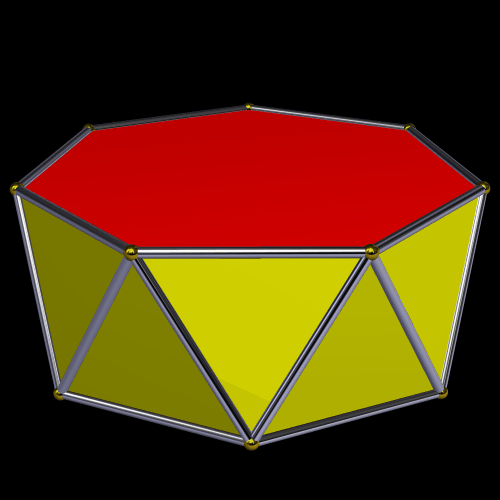
Here’s an octagonal antiprism.
Next, the dual of this antiprism: a trapezohedron. Its faces are sixteen kites.
If you stellate this trapezohedron twice, you get a two-part compound.
Now, the compound of the octagonal antiprism and its dual.
The next thing I did was to form the convex hull of this compound.
The next thing I did was to examine this convex hull’s dual.
Lastly, I stellated this dual once.
I did all of this using Stella 4d: Polyhedron Navigator. You can try this software for free at http://www.software3d.com/Stella.php.
Four Polyhedra, Each With Seven-Fold Dihedral Symmetry
First, the heptagonal antiprism.
The rest of the polyhedra in this post were made from this antiprism, using the functions available in Stella 4d: Polyhedron Navigator, such as stellation and faceting. If you’d like to try this program yourself, you can do so, free, at http://www.software3d.com/Stella.php.
Two Views of a Paper Model of an Icosidodecahedron
Two Views of a Paper Model of the Great Dodecahedron
The obtuse triangles here are golden gnomons, which are isosceles triangles with vertex angles of 108 degrees, as well as base-to-leg ratios which are golden. These triangles are facelets; the actual, much larger faces are the regular pentagons of which the golden gnomons are parts. In this model, all facelets which are part of the same (or parallel) faces are all one color, with six colors of paper used, in all, for this non-convex, twelve-faced, regular polyhedron, which is one of the Kepler-Poinsot solids.
Much of each face is hidden from view in this polyhedron’s interior — or rather, this is the case for the mathematical construct called the great dodecahedron. This physical model, on the other hand, is hollow on the inside. One is made only of ideas, while the other is made of atoms.
No computer programs were involved in the construction of this model. It was made using compass, straight edge, scissors, card stock, pencils, and tape.
The Return of Paper Polyhedra

Clockwise from bottom right, these polyhedra are the cuboctahedron, the rhombic triacontahedron, the rhombic dodecahedron, the compound of the cube and the octahedron, and the rhombicosidodecahedron. They were made using card stock, compass, straightedge, scissors, and tape. Since I started blogging polyhedra, I’ve made most of my models using software, and quite a few using Zome. Making paper models was something I used to do . . . until a couple of days ago, when, on a lark, I made the cuboctahedron you see here. Bitten by the bug, I then made the other four models yesterday and today. There’s something satisfying about returning to the basics now and then.
A Great Stellated Dodecahedron, Augmented With More Great Stellated Dodecahedra
I made this using Stella 4d, which you can try for free here.