Tag Archives: rhombicosidodecahedron

Two Different Clusters of Thirty-One Rhombicosidodecahedra

Posted on by
Reply

31 RID version A

The cluster above was formed by starting with one rhombicosidodecahedron, and then augmenting each of its thirty square faces with another rhombicosidodecahedron. If you examine the single rhombicosidodecahedron below, though, you’ll see that this can be done in two different ways, each of which produces a cluster with the same degree of symmetry as the original. (If less symmetry is acceptable, there are far more than two different ways to obtain such clusters, but that does not interest me.)

Rhombicosidodeca

When new rhombicosidodecahedra are attached to the square faces of this central rhombicosidodecahedron, they new ones can be oriented such that pentagons are placed above pentagons, and triangles above triangles — or the new ones can be oriented the other way, so that pentagons are placed above triangles, and triangles above pentagons. One of these possibilities produces the cluster at the top of this post. The other possibility produces the cluster shown below.

31 RID version BAll of these polyhedral manipulations were performed using a program called Stella 4d: Polyhedron Navigator, which may be purchased (or tried for free, as a trial download) at http://www.software3d.com/Stella.php.

A Halloween Rhombicosidodecahedron

Posted on by
2

Rhombicosidodeca

This Jack-o-Lantern picture was found with a Google image-search, and then I projected it onto a rhombicosidodecahedron, and created this rotating .gif file, using Stella 4d — a program available at http://www.software3d.com/Stella.php. Happy Halloween!

One of Many Possible Facetings of the Rhombicosidodecahedron

Posted on by
Reply

Faceted Rhombicosidodeca

I created this using Stella 4d:  Polyhedron Navigator, available at www.software3d.com/Stella.php. Faceting involves connecting different sets of vertices (relative to the original polyhedron) to form new edges and faces. The new edges and faces, both, typically intersect each other, although often not as many times as in this particular example of a faceted polyhedron. 

A Simulation of Crystalline Growth Using Polyhedral Augmentation

Posted on by
Reply

Crystals and crystalline growth have been studied for centuries because of, at least in part, their symmetry. Crystals are cut in such a way as to increase this symmetry even more, because most people find symmetry attractive. However, where does the original symmetry in a crystal come from? Without it, jewelers who cut gemstones would not exist, for the symmetry of crystalline minerals themselves is what gives such professionals the raw materials with which to work.

To understand anything about how crystals grow, one must look at a bit of chemistry. The growth of crystals:

  • Involves very small pieces:  atoms, molecules, ions, and/or polyatomic ions
  • Involves a small set of simple rules for how these small pieces attach to each other

Why small pieces? That’s easy:  we live in a universe where atoms are tiny, compared to anything we can see. Why is the number of rules for combining parts small, though? Well, in some materials, there are, instead, large numbers of ways that atoms, etc., arrange themselves — and when that happens, the result, on the scale we can see, is simply a mess. Keep the number of ways parts can combine extremely limited, though, and it is more likely that the result will possess the symmetry which is the source of the aesthetic appeal of crystals.

This can be modeled, mathematically, by using polyhedral clusters. For example, I can take a tetrahedron, and them augment each of its four faces with a rhombicosidodecahedron. The result is this tetrahedral cluster:

Image

Next, having chosen my building blocks, I need a set of rules for combining them. I choose, for this example, these three:

  1. Only attach one tetrahedral cluster of rhombicosidodechedra to another at triangular faces — and only use those four triangles, one on each rhombicosidodecahedron, which are at the greatest distance from the cluster’s center.
  2. Don’t allow one tetrahedral cluster to overlap another one.
  3. When you add a tetrahedral cluster in one location, also add others which are in identical locations in the overall, growing cluster.

Using these rules, the first augmentation produces this:

Image

That, in turn, leads to this:

Image

Next, after another round of augmentation:

Image

One more:

Image

In nature, of course, far more steps than this are needed to produce a crystal large enough to be visible. Different crystals, of course, have different shapes and symmetries. How can this simulation-method be altered to model different types of crystalline growth? Simple:  use different polyhedra, and/or change the rules you select as augmentation guidelines, and you’ll get a different result.

[Note:  all of these images were created using Stella 4d: Polyhedron Navigator. This program is available at http://www.software3d.com/Stella.php.]

 

Five of the Thirteen Archimedean Solids Have Multiple English Names

Image

Reply

Four Archimedean Solids with Multiple English Names

I call the polyhedron above the rhombcuboctahedron. Other names for it are the rhombicuboctahedron (note the “i”), the small rhombcuboctahedron, and the small rhombicuboctahedron. Sometimes, the word “small,” when it appears, is put in parentheses. Of these multiple names, all of which I have seen in print, the second one given above is the most common, but I prefer to leave the “i” out, simply to make the word look and sound less like “rhombicosidodecahedron,” one of the polyhedra coming later in this post.

Trunc Cubocta

My preferred name for this polyhedron is the great rhombcuboctahedron, and it is also called the great rhombicuboctahedron. The only difference there is the “i,” and my reasoning for preferring the first name is the same as with its “little brother,” above. However, as with the first polyhedron in this post, the “i”-included version is more common than the name I prefer.

Unfortunately, this second polyhedron has another name, one I intensely dislike, but probably the most popular one of all — the truncated cuboctahedron. Johannes Kepler came up with this name, centuries ago, but there’s a big problem with it: if you truncate a cuboctahedron, you don’t get square faces where the truncated parts are removed. Instead, you get rectangles, and then have to deform the result to turn the rectangles into squares. Other names for this same polyhedron include the rhombitruncated cuboctahedron (given it by Magnus Wenninger) and the omnitruncated cube or cantitruncated cube (both of these names originated with Norman Johnson). My source for the named originators of these names is the Wikipedia article for this polyhedron, and, of course, the sources cited there.

Rhombicosidodeca

This third polyhedron (which, incidentally, is the one of the thirteen Archimedean solids I find most attractive) is most commonly called the rhombicosidodecahedron. To my knowledge, no one intentionally leaves out the “i” after “rhomb-” in this name, and, for once, the most popular name is also the one I prefer. However, it also has a “big brother,” just like the polyhedron at the top of this post. For that reason, this polyhedron is sometimes called the small rhombicosidodecahedron, or even the (small) rhombicosidodecahedron, parentheses included.

Trunc Icosidodeca

I call this polyhedron the great rhombicosidodecahedron, and many others do as well — that is its second-most-popular name, and identifies it as the “big brother” of the third polyhedron shown in this post. Less frequently, you will find it referred to as the rhombitruncated icosidodecahedron (coined by Wenninger) or the omnitruncated dodecahedron or icosahedron (names given it by Johnson). Again, Wikipedia, and the sources cited there, are my sources for these attributions.

While I don’t use Wenninger’s nor Johnson’s names for this polyhedron, their terms for it don’t bother me, either, for they represent attempts to reduce confusion, rather than increase it. As with the second polyhedron shown above, this confusion started with Kepler, who, in his finite wisdom, called this polyhedron the truncated icosidodecahedron — a name which has “stuck” through the centuries, and is still its most popular name. However, it’s a bad name, unlike the others given it by Wenninger and Johnson. Here’s why: if you truncate an icosidodecahedron (just as with the truncation of a cuboctahedron, described in the commentary about the second polyhedron pictured above), you don’t get the square faces you see here. Instead, the squares come out of the truncation as rectangles, and then edge lengths must be adjusted in order to make all the faces regular, once more. I see that as cheating, and that’s why I wish the name “truncated icosidodecahedron,” along with “truncated cuboctahedron” for the great rhombcuboctahedron, would simply go away.

Here’s the last of the Archimedean solids with more than one English name:

Trunc Cube

Most who recognize this shape, including myself, call it the truncated cube. A few people, though, are extreme purists when it comes to Greek-derived words — worse than me, and I take that pretty far sometimes — and they won’t even call an ordinary (Platonic) cube a cube, preferring “hexahedron,” instead. These same people, predictably, call this Archimedean solid the truncated hexahedron. They are, technically, correct, I must admit. However, with the cube being, easily, the polyhedron most familiar to the general public, almost none of whom know, let alone use, the word “hexahedron,” this alternate term for the truncated cube will, I am certain, never gain much popularity.

It is unfortunate that five of the thirteen Archimedean solids have multiple names, for learning to spell and pronounce just one name for each of them would be task enough. Unlike in the field of chemistry, however, geometricians have no equivalent to the IUPAC (International Union of Pure and Applied Chemists), the folks who, among other things, select official, permanent names and symbols for newly-synthesized elements. For this reason, the multiple-name problem for certain polyhedra isn’t going away, any time soon.

(Image credit:  a program called Stella 4d, available at www.software3d.com/Stella.php, was used to create all of the pictures in this post.)

The Seven Zonish Rhombicosidodecahedra Based On Symmetry Axes

Image

Reply

Zonish Versions of the Rhombicosidodecahedron

The top image here is of a zonish polyhedron based on adding zones along the five-fold symmetry axes of a rhombicosidodecahedron. All its edges are the same length, and its 62 faces include thirty elongated octagons, twelve regular pentagons, and twenty triangles. All of its edges have the same length.

The edges of this next polyhedron are also all of the same length. It was made in the same way, except that zones were added along both three- and five-fold symmetry axes of a rhombicosidodecahedron. Its 182 faces include thirty elongated dodecagons, twenty triangles, twelve regular pentagons, sixty squares, and sixty rhombi.

182 faces incl 30 elongated dodecagons and 12 pentagons and 60 squares and sixty rhombi and twenty triangles

If only the three-fold symmetry axes are used to make a zonish polyhedron from a rhombicosidodecahedron, this next polyhedron, also with all edge lengths equal, is the result. It also has 182 faces, and they are of the same type as in the one immediately before, except that thirty elongated octagons replace the dodecagons from that polyhedron.

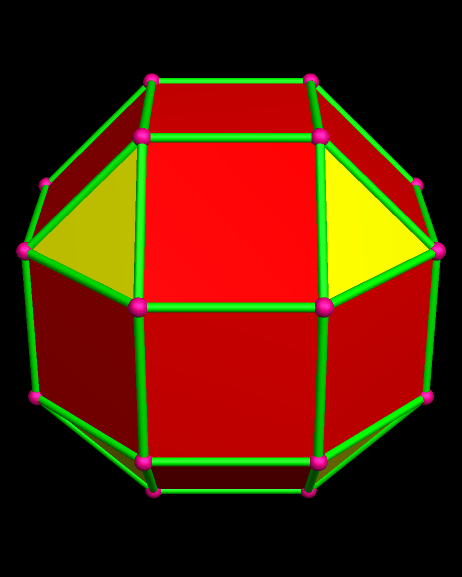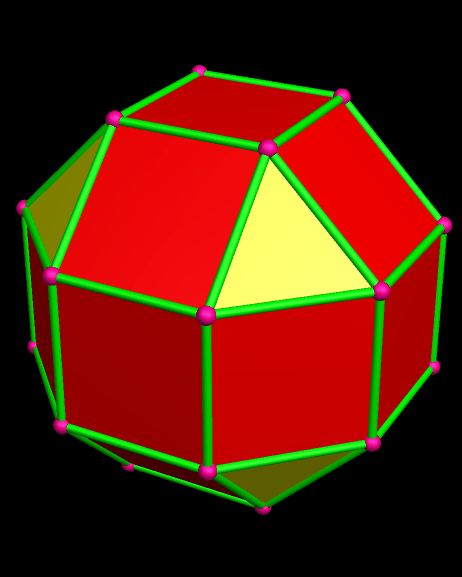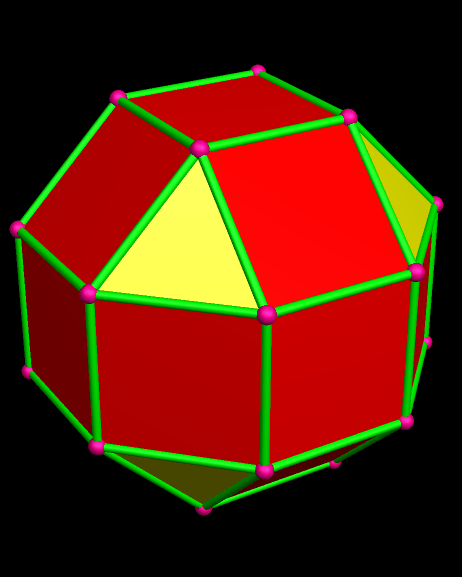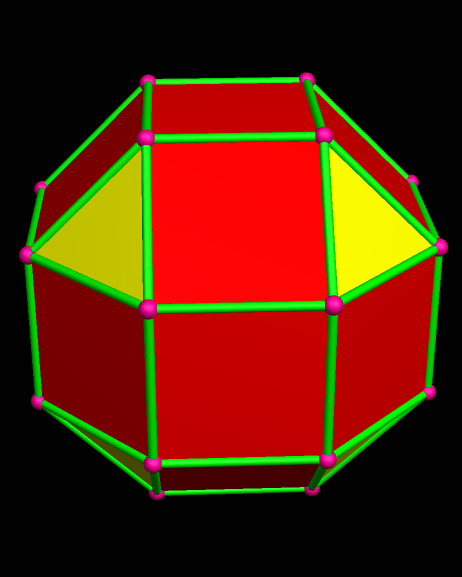
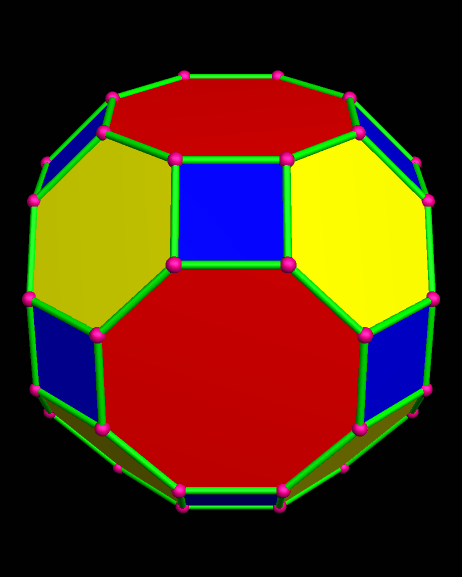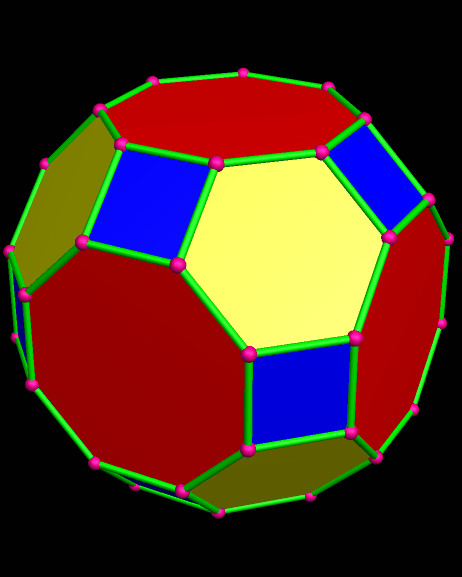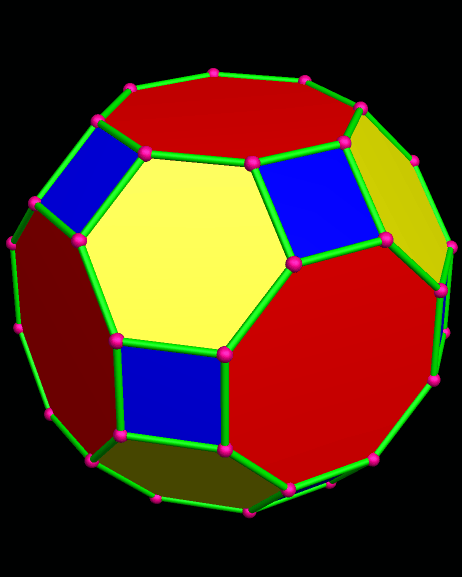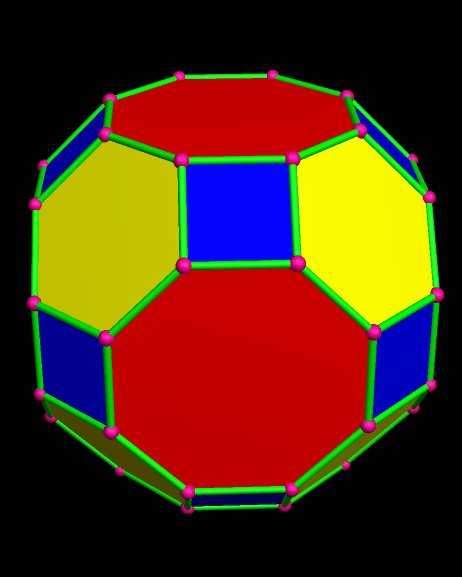
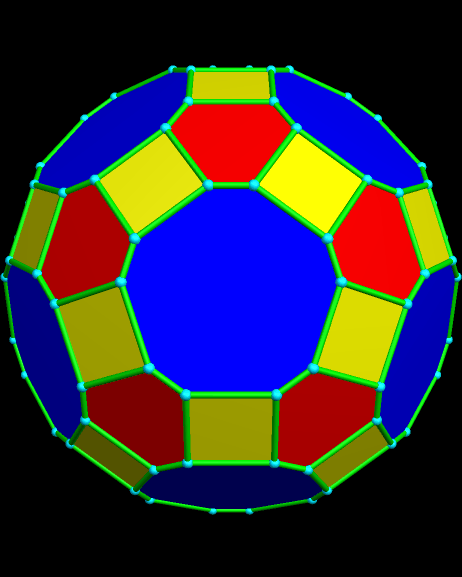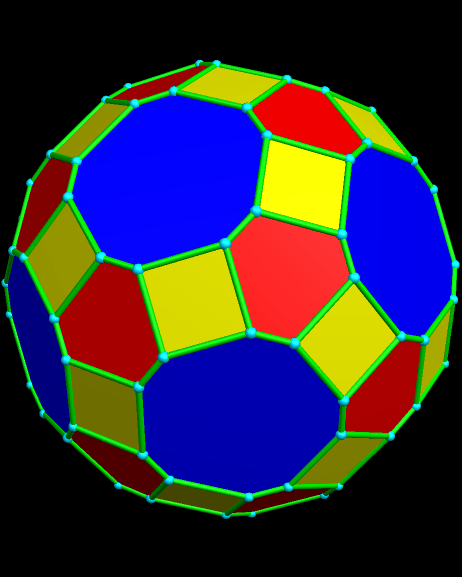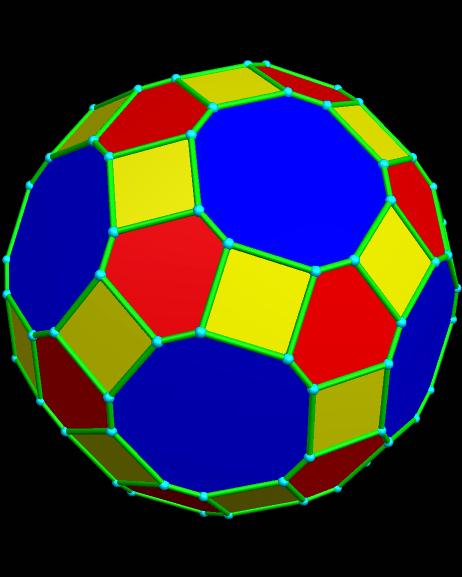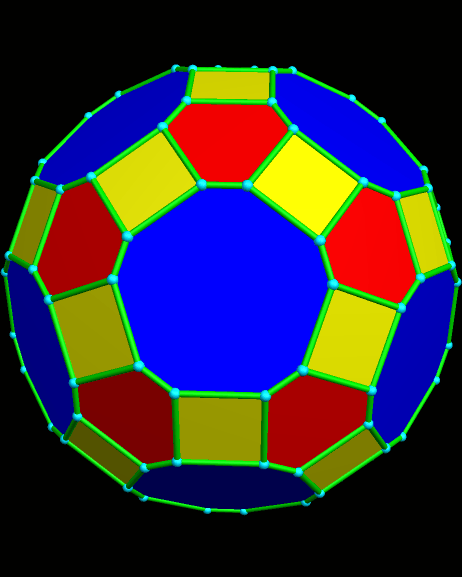
zonish rid

A rhombicosidodecahedron also has two-fold symmetry axes. If only those axes are used to make a zonish rhombicosidodecahedron, this next polyhedron is the result:  a modified form of the great rhombicosidodecahedron, with unequal edge lengths.

zonish rid

If the two- and three-fold symmetry axes are both used, the result, once again, is a 182-faces polyhedron, but it also has unequal edge lengths, and none of its faces are regular polygons. It is shown below. There are twelve decagons, sixty rectangles, sixty hexagons of one type, twenty hexagons of another type,  and thirty octagons.

zonish rid

Another possible combination is to use the two- and five-fold symmetry axes to create a zonish rhombicosidodecahedron. This yields a polyhedron with 122 faces, with all except the sixty squares being irregular. The other faces are twelve decagons, thirty octagons, and twenty hexagons:

zonish rid

Finally, there is one last combination — using the two-, three-, and five-fold symmetry axes, all at once. Here’s what it looks like:

zonish rid

As one should expect, this produces a zonish polyhedron with more faces than any of the earlier ones shown above: 242 in all. As in the last one shown, only the sixty squares are regular, although the sixty pink hexagons are at least equilateral. There are also sixty rectangles, twenty hexagons of a second type, thirty dodecagons, and twelve decagons.

All of these zonish rhombicosidodecahedra were created using Stella 4d, software available at http://www.software3d.com/Stella.php.

A Torus, Composed of Fifteen Interpenetrating Rhombicosidodecahedra

Image

Reply

A Torus, Composed of Fifteen Interpenetrating Rhombicosidodecahedra

Software credit: I used Stella 4d to make this, which is available at http://www.software3d.com/Stella.php.

The Origin of an Interplanetary War: Itaumiped vs. Almausoped

Image

3

The Origin of an Interplanetary War: Itaumiped vs. Almausoped

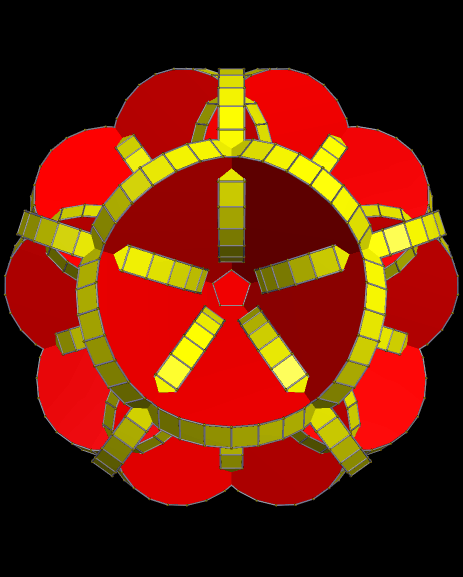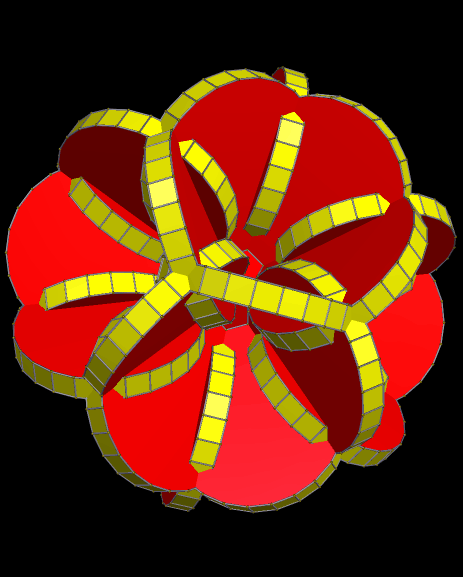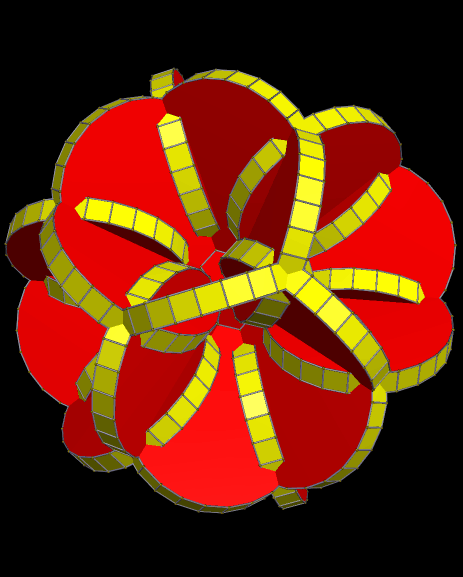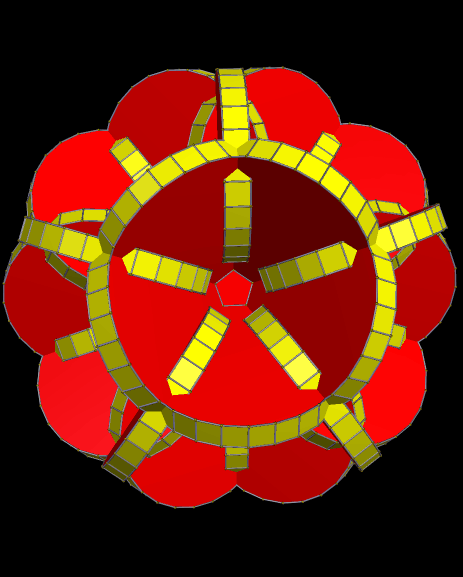
Itaumiped and Almausoped are artificial rogue planets, each an identical member of a double-planet system bound into orbit, and tidally-locked, by gravity. The energy source used by the planets’ inhabitants, which uses a radioactive isotope with a very long half-life, causes the faces of these hollow polyhedral planets to radiate heat and light, both on the inside and outside, which is why you can see them here, but do not see a “night” side on either planet.

Long ago, the common ancestors of the Itaumipedeans and the Almausopedeans, living on the natural planet Loorohmude where their species evolved, built each of these planets as a heavily-populated, multi-generational, interstellar colony-ship. They built two, using materials from large asteroids, and launched them together, for a perfectly good reason: if something happened to one of the planet-ships, the survivors could find refuge in the other one. A large pentagonal hole was even built into each planet’s polyhedral design, and set to face the other one, simply to allow ease of communication, and travel, between them. Their journey was to last “only” twelve generations . . . but things don’t always go as planned.

An idea took root, and spread during the long journey, that viewed the old stories of Loorohmude as primitive, dangerous superstitions, with no evidence to support their veracity — other than ancient written records, which the anti-Loorohmudeans viewed as dangerous fabrications. Civil war broke out on each planet, and the anti-Loorohmudeans achieved two of their goals: they killed a lot of their enemies (who returned the favor in kind), and they destroyed the ancient records, despite the attempts of their enemies to save them. On each planet, some of the inhabitants on each side survived — but, on both, the old records were utterly obliterated.

The information lost wasn’t all mere history for history’s sake, but also included essential technical material, such as instructions for building the device, while in transit, which would allow Itaumiped and Almausoped to slow their velocity in time to achieve orbit when they reached their destination, the distant planet Stidennatio. For this reason, this planned deceleration never happened, and the twin war-ravaged planets flew right past Stidennatio at a high fraction of the speed of light. Inertia carried them right through Stidennatio’s solar system, and into the uncharted space beyond. With civil wars still raging on each planet, however, the combatants took little notice of the solar system they rapidly flew through, and those few who did notice any of it did not understand what they were seeing.

The reduced populations of each planet, simply due to their smaller numbers, now had supplies for a much longer journey, and eventually, the civil wars stopped . . . because both sides ran out of long-range weapons. They could have continued fighting without weapons, or with such things as knives and clubs . . . but by that time, the population was so reduced, so dispersed, and so war-weary, that hostilities on each side simply dwindled slowly away.

It took a long time — just under three generations — for the smoke to clear, and the population to start to rebound. By this time, no one thought of themselves as pro- or anti-Loorohmudeans anymore, but simply as the descendants of the survivors of a terrible war.

Naturally, and gradually, everyone started looking for someone to blame for the atrocities that always accompany warfare. By this time, the ravages of war had rendered the exterior surfaces of both Itaumiped and Almausoped uninhabitable, so everyone lived in the hollow interiors of each planet-ship. From this inside vantage point, thanks to the pentagonal holes which were part of the original design, everyone could see one convenient scapegoat: the other planet, always in view, and close enough that evidence of habitatation could be seen with telescopes.

Lasers aren’t all that difficult to make, and so the first shot fired in the new, second period of warfare, between the planets this time, took the form of an intense pulse-laser blast exiting one pentagonal hole, and entering its counterpart. It destroyed the top of an abandoned building, and killed no one . . . but it was noticed, and so a retaliatory strike soon took the same path, but in the opposite direction. This time, there were fatalities. More weapons were built, and immediately deployed. Soon, full-scale interplanetary war was raging.

This new war won’t last forever. It may stop when supplies run out, to be followed by famine, or the supplies might hold out until everyone simply kills each other. Does it matter which of these outcomes happens? No, not really. Itaumiped and Almausoped passed their destination generations ago, and now they’re going nowhere, at a high rate of speed . . . in more than one way.

Unlike their inhabitants, though, the planet-ships Itaumiped and Almausoped, soon to be devoid of life, will continue much longer. Just as they have since their construction, they will keep orbiting their common center of mass, and keep getting further away from their original, long-forgotten launch point, as well as their intended destination, until the heat death of the universe finally catches up with them, as well.

###

Notes: Itaumiped (anagram for “I made it up”) and Almausoped (anagram for “also made up”) have different characteristics every time they appear. This is one of the nicer things about having my own imaginary astronomical objects — I don’t have to memorize things like planetary radius, mass, etc., because, since they’re mine to play with as I please, I can change their features according to my whims. For example, Almausoped was always previously depicted as the star orbited by Itaumiped. In this incarnation, however, there’s no star around. Also, Loorohmude is an anagram for “our old home,” and Stidennatio is an anagram for “destination.” The image that accompanies this story was created using Stella 4d, which you may try or buy at http://www.software3d.com/Stella.php.

A Rhombicosidodecahedron, Augmented with Thirty Icosakaipentagonal Prisms

Image

Reply

A Rhombicosidodecahedron, Augmented with Thirty Icosagonal Prisms

When adding icosakaipentagonal prisms (those where the bases have 25 sides) to the thirty square faces of a rhombicosidodecahedron, the prisms can have one of two orientations. One is above, and here is the other one (click to enlarge):

Augmented Rhombicosidodeca

Software credit: I made these images using Stella 4d, available at http://www.software3d.com/Stella.php (free trial download available).

A Cubic Cluster of Rhombicosidodecahedra

Image

Reply

A Cubic Cluster of Rhombicosidodecahedra

I made this, using Stella 4d, by augmenting each face of an octahedron with a rhombicosidodecahedron. You can give this program a try yourself, for free, at http://www.software3d.com/stella.php.