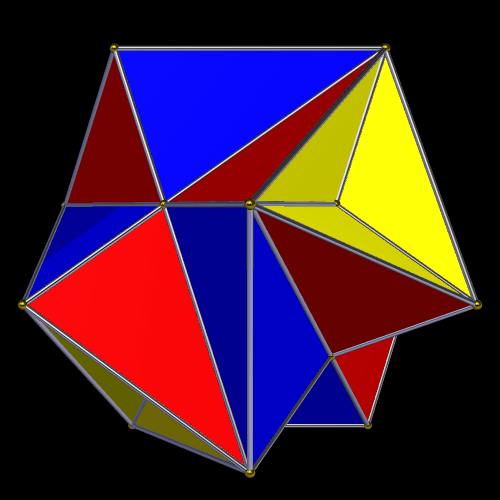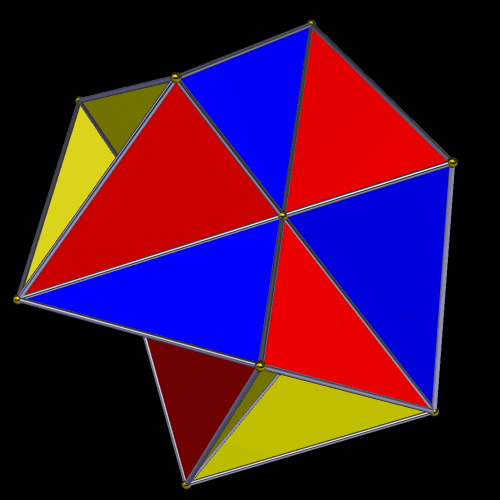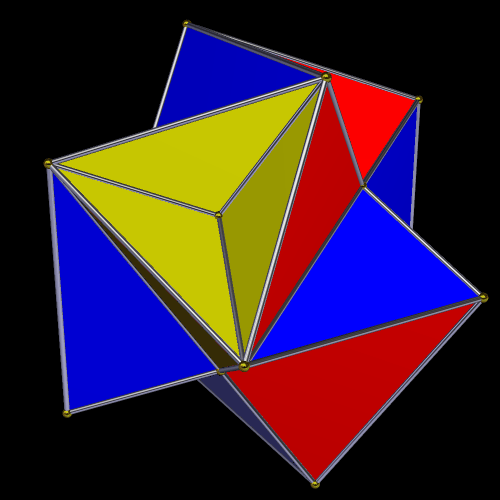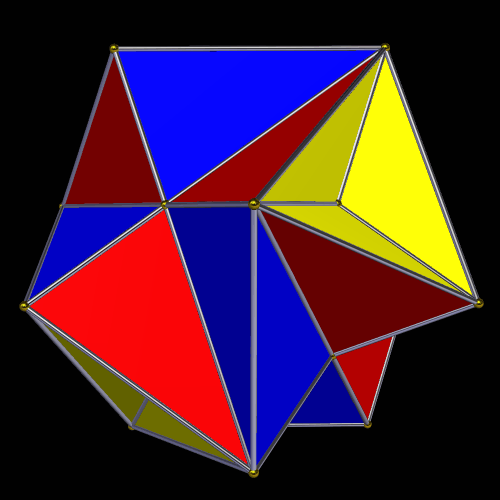
To make this polyhedron, I first changed the symmetry-type of a dodecahedron from icosahedral to tetrahedral, then stellated it twice. This was done using Stella 4d, a program you may try for free at http://www.software3d.com/Stella.php.
If you stellate the snub dodecahedron 43 times, this is the result. The yellow faces are kites, not rhombi.
Like the snub dodecahedron itself, this polyhedron is chiral. Here is the mirror-image of the polyhedron shown above.
Any chiral polyhedron may be combined with its own mirror-image to create a compound.
This is the dual of the snub dodecahedron’s 43rd stellation.
This dual is also chiral. Here is its reflection.
Finally, here is the compound of both duals.
I used Stella 4d: Polyhedron Navigator to create these images. You may try this program for yourself at http://www.software3d.com/Stella.php.
I made this using Stella 4d: Polyhedron Navigator, which you may try for free right here.
This is the truncated dodecahedron. It is one of the Archimedean solids.
This polyhedron has a long stellation-series, from which I selected several on aesthetic grounds. The figure immediately below is the truncated dodecahedron’s 16th stellation.
Here is the 21st stellation.
It’s easy to stellate polyhedra rapidly, and make many other changes to them, with Stella 4d: Polyhedron Navigator. You can try it for free at http://www.software3d.com/Stella.php.
The stellation shown immediately above is the 25th, and the one shown immediately below is the 27th.
Here is the next stellation: the 28th. Unlike the ones shown above, it is chiral.
This is the truncated dodecahedron’s 31st stellation.
This one is the 38th stellation.
This one is the 44th.
The last one shown here is called the truncated dodecahedron’s final stellation because, if it is stellated once more, it returns to the original truncated dodecahedron.
I created these with Stella 4d, which you may try for free at this website. To make a given polyhedral stellation appear larger, simply click on it.
The polyhedron above is the 12th stellation of the truncated cube. The one below is the 14th.
The next one shown is the 18th and final stellation. If stellated again, the result is an ordinary truncated cube.
These virtual models were made using Stella 4d, software you may try for yourself at http://www.software3d.com/Stella.php.
This is a pentagonal hexacontahedron, the dual of the snub dodecahedron. It’s decorated with mandalas of the the type I blogged here, two posts ago. The mandalas do interesting things when this polyhedron is stellated, as you can see below.
That was the first stellation, and here is the second:
The sixth stellation was the last one I found interesting enough to post.
All four polyhedral images above were created using Stella 4d: Polyhedron Navigator, software you may buy, or try for free, at this website.
This is the icosahedron, followed by its first stellation.
The first stellation of the icosahedron can be stellated again, and again, and so on. The “final stellation” of the icosahedron is the one right before the stellation-series “wraps around,” back to where it started:
This final stellation of the icosahedron would serve pretty well as a “polyhedral porcupine,” but I was seeking something even better, so I turned my attention to polyhedral compounds. This is the compound of five icosahedra:
The program I use to manipulate these solids is called Stella 4d: Polyhedron Navigator (free trial download available here). My next move, using Stella, was to create the final stellation of this five-icosahedron compound . . . and, when I saw it, I knew I had found my “polyhedral porcupine.”
The stellation-series of the truncated dodecahedron contains some interesting polyhedra. Selections from this series appear below.
The polyhedron above is the 24th stellation of the truncated dodecahedron, while the one below is the 25th stellation.
The polyhedron immediately above is the truncated dodecahedron’s 27th stellation. The one shown below is the 29th stellation.
The last two polyhedra in this post are the truncated dodecahedron’s 36th stellation (above), and its 70th stellation (below).
These images were created using Stella 4d, software available here.
First, this is the 11th stellation.
Next, the 13th:
And, finally, the 15th stellation of the icosahedron:
I used Stella 4d, which you can find here, to make these.
RobertLovesPi.net 