I made this compound using software called Stella 4d: Polyhedron Navigator. This program may be purchased (or a trial download tried for free) at this website.
Tag Archives: stellation
Flying Kites into the Snub Dodecahedron, a Dozen at a Time, Using Tetrahedral Stellation
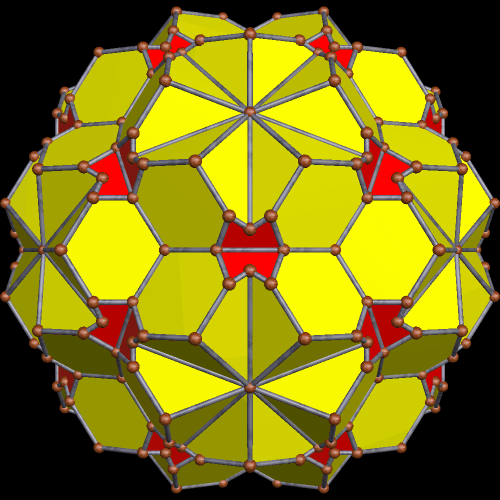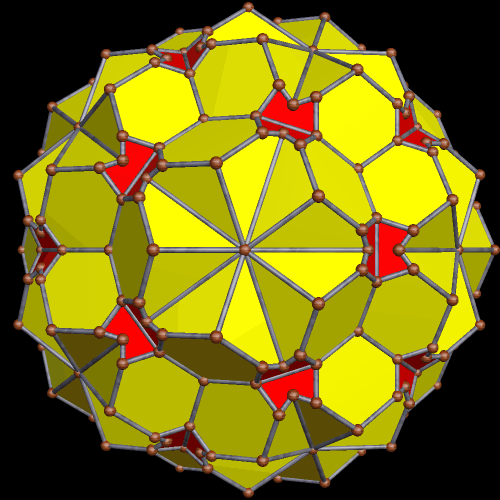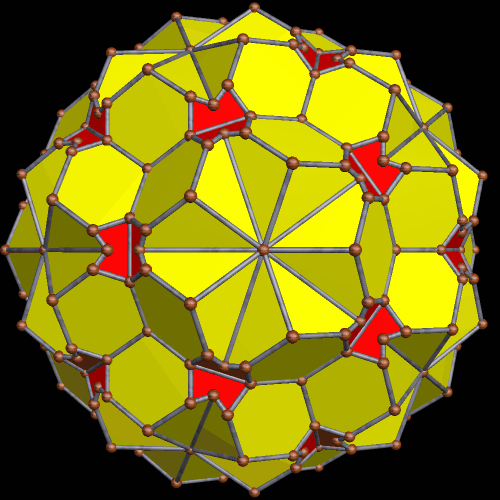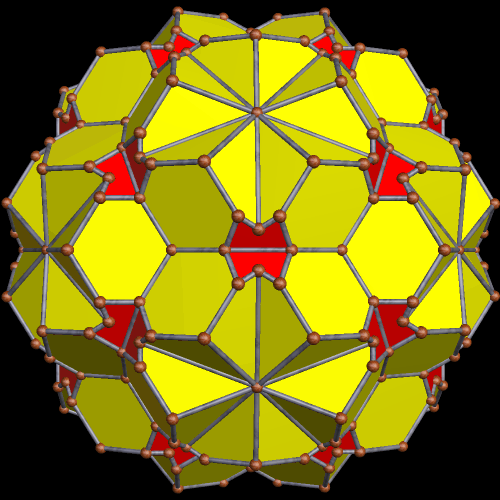
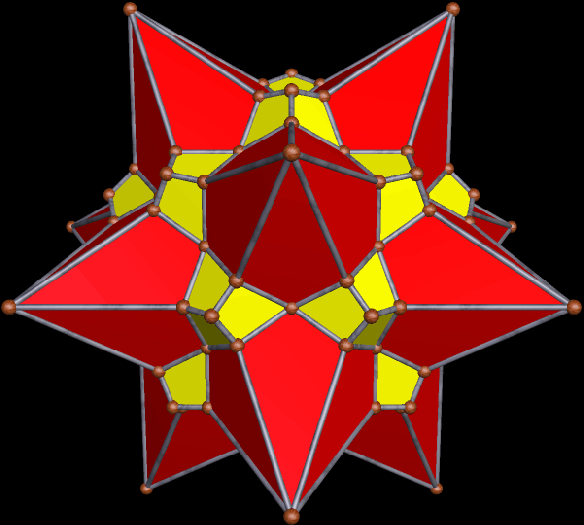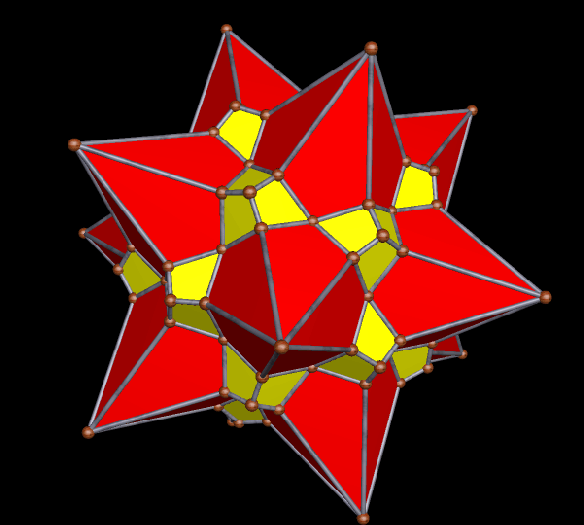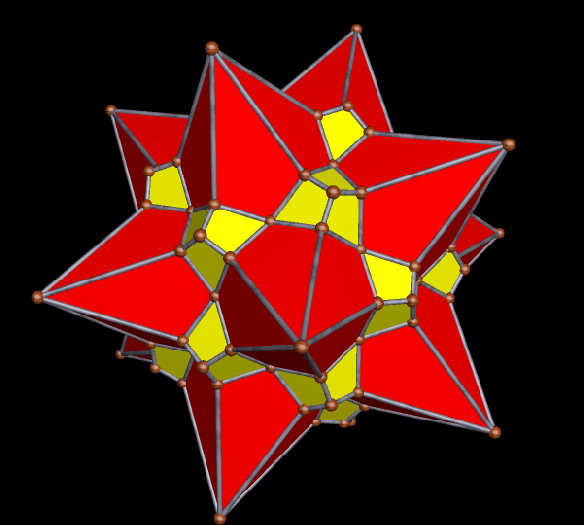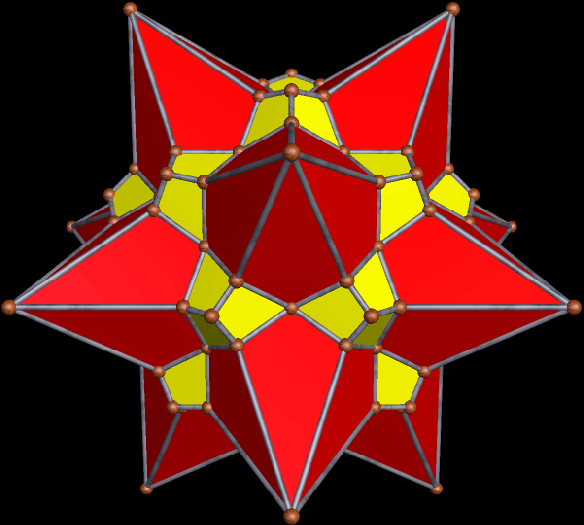
I’ve been shown, by the program’s creator, a function of Stella 4d which was previously unknown to me, and I’ve been having fun playing around with it. It works like this: you start with a polyhedron with, say, icosidodecahedral symmetry, set the program to view it as a figure with only tetrahedral symmetry (that’s the part which is new to me), and then stellate the polyhedron repeatedly. (Note: you can try a free trial download of this program here.) Several recent posts here have featured polyhedra created using this method. For this one, I started with the snub dodecahedron, one of two Archimedean solids which is chiral.
Using typical stellation (as opposed to this new variety), stellating the snub dodecahedron once turns all of the yellow triangles in the figure above into kites, covering each of the red triangles in the process. With “tetrahedral stellation,” though, this can be done in stages, producing a greater variety of snub-dodecahedron variants which feature kites. As it turns out, the kites appear twelve at a time, in four sets of three, with positions corresponding to the vertices (or the faces) of a tetrahedron. Here’s the first one, featuring one dozen kites.
Having done this once (and also changing the colors, just for fun), I did it again, resulting in a snub-dodecahedron-variant featuring two dozen kites. At this level, the positions of the kite-triads correspond to those of the vertices of a cube.
You probably know what’s coming next: adding another dozen kites, for a total of 36, in twelve sets of three kites each. At this point, it is the remaining, non-stellated four-triangle panels, not the kite triads, which have positions corresponding to those of the vertices of a cube (or the faces of an octahedron, if you prefer).
Incoming next: another dozen kites, for a total of 48 kites, or 16 kite-triads. The four remaining non-stellated panels of four triangles each are now arranged tetrahedrally, just as the kite-triads were, when the first dozen kites were added.
With one more iteration of this process, no triangles remain, for all have been replaced by kites — sixty (five dozen) in all. This is also the first “normal” stellation of the snub dodecahedron, as mentioned near the beginning of this post.
From beginning to end, these polyhedra never lost their chirality, nor had it reversed.
There Are Many Faceted Versions of the Dodecahedron. This One Is the Dual of the Third Stellation of the Icosahedron.
The twelve purple faces of this faceted dodecahedron show up on Stella 4d‘s control interface as {10/4} star decagons, which would make them each have five pairs of two coincident vertices. I’m informally naming this special decagon-that-looks-like-a-pentagram (or “star pentagon,” if you prefer) the “antipentagram,” for reasons which I hope are clear.
Stella 4d, the program I use to make most of my polyhedral images, may be tried for free at http://www.software3d.com/Stella.php.
Selections from the Second Hundred Stellations of the Rhombicosidodecahedron
This survey began in the last post, with selections from the first hundred stellations of this Archimedean solid. In this survey of the second hundred stellations, the first one I find noteworthy enough for inclusion here is the 102nd stellation.
A similar figure is the 111th stellation:
There followed a long “desert” when I did not find any that really “grabbed” me . . . and then I came to the 174th stellation.
The fact that it is monocolored, the way I had Stella 4d set, told me immediately that this stellation (the one above) has only one face-type. There are twenty of these faces; they are each equilateral hexagons which “circumscibe,” in a way, the triangular faces of an icosahedron. For this reason, I suspect this is also one of the stellations of the icosahedron; I’m making a mental note to do exactly that.
I also make a second virtual model of the 174th stellation of the rhombicosidodecahedron, with the faces colored in such a way as to make the interpenetrating equilateral hexagons more obvious.
After that interesting stellation, the next one to caught my attention is the 179th stellation.
Next of note, the 182nd stellation is similar to the icosahedron/dodecahedron compound, but with the dodecaheron larger than it is in that compound, so that edges, one from each component polyhedron, do not intersect, but are instead skew. Another way to view it is that the dodecahedron is encasing the icoahedron, but with enough room left for portions of the icosahedron to protrude from the faces of the “dodecahedral cage.”
Next is the 183rd stellation.
Here is the 187th stellation, which is quite similar to the last one shown. The pulsating effect, first seen in the last post above, is an accident, and not discovered until after these images were already made, using Stella 4d, which may be tried here. Why didn’t I re-create the .gifs? Simple: I don’t feel like taking the ~10 minutes each to do so.
The 190th stellation may also be viewed as a dodecahedron, augmented with variations of pentagonal pyramids on each face:
Next, the 191st stellation:
And, after that, the 192nd stellation.
The next stellation which grabbed by attention: the 198th.
Finally, I’ll close this set of highlights from this part of the rhombicosidodecahedron’s stellation-series with that solid’s 199th stellation.
Selections from the First Hundred Stellations of the Rhombicosidodecahedron
Since shortly after I learned of their existence, I have found the rhombicosidodecahedron to be the most attractive of the Archimedean solids. That’s a personal aesthetic statement, of course, not a mathematical one.
This solid has a long stellation-series. With Stella 4d, the program I used to make these images, it’s easy to simply scroll through them. The stellation of this polyhedron follows these stellation-diagrams; I used Stella 4d to make them as well. You may research, try, or buy this program at this website. The first of these stellation-diagrams is for the planes of the twelve pentagonal faces.
For the planes of the twenty triangular faces, this is the stellation-diagram:
 Finally, there are the the planes of the thirty square faces.
Finally, there are the the planes of the thirty square faces.
The following survey of the first hundred stellations is not intended to be exhaustive; I’m including all those I find worthy of inclusion on subjective aesthetic grounds. The first stellation shown here is actually the 25th stellation of the rhombicosidodecahedron:
Next, the 30th stellation:
The next one is the 33rd stellation.
And next, the 38th stellation.
Here is the 46th stellation:
And the 48th stellation:
Next, the 58th stellation:
And now, the 62nd stellation.
Next is the 85th stellation; it’s also a compound of an icosahedron (blue), and a yellow polyhedron I have not yet identified, except as the nth stellation of something. This I know: I have seen the yellow polyhedron before. If you happen to know what it is, the identify it in a comment.
The next stellation shown is the next one in the series, the 86th. It demonstrates a phenomenon I have observed, but cannot explain, and that is the tendency, in sequences of stellations, to have a large number of similar stellations in a row, followed by a sudden, much more extreme change in appearance, from one stellation to the next, as seen here. It’s a phenomenon which I would like to better understand.
To be continued, with selections from the next hundred stellations….
The Final Stellation of the Great Rhombicosidodecahedron, Together with Its Dual
In the last post, several selections from the stellation-series of the great rhombicosidodecahedron (which some people call the truncated icosidodecahedron) were shown. It’s a long stellation-series — hundreds, or perhaps thousands, or even millions, of stellations long (I didn’t take the time to count them) — but it isn’t infinitely long. Eventually, if repeatedly stellating this polyhedron, one comes to what is called the “final stellation,” which looks like this:
Stellation-series “wrap around,” so if this is stellated one more time, the result is the (unstellated) great rhombicosidodecahedron. In other words, the series starts over.
The dual of the great rhombicosidodecahedron is called the disdyakis triacontahedron. The reciprocal function of stellation is faceting, so the dual of the figure above is a faceted disdyakis triacontahedron. Here is this dual:
To complicate matters further, there is more than one set of rules for stellation. For an explanation of this, I refer you to this Wikipedia page. In this post, and the one before, I am using what are known as the “fully supported” rules.
Both these images were made using Stella 4d, software you can buy, or try for free, right here. When stellating polyhedra using this program, it can be set to use different rules for stellation. I usually leave it set for the fully supported stellation criteria, but other polyhedron enthusiasts have other preferences.
Selections from the Stellation-Series of the Great Rhombicosidodecahedron
The great rhombicosidodecahedron, also known as the truncated icosidodecahedron, has a long and complex stellation series. Here are some highlights from that series, chosen using aesthetic, rather than mathematical, criteria.
All these virtual models were made using Stella 4d, which you can try and/or buy here.
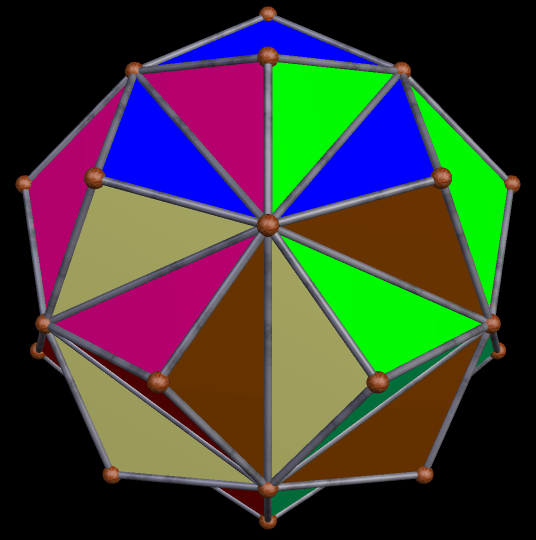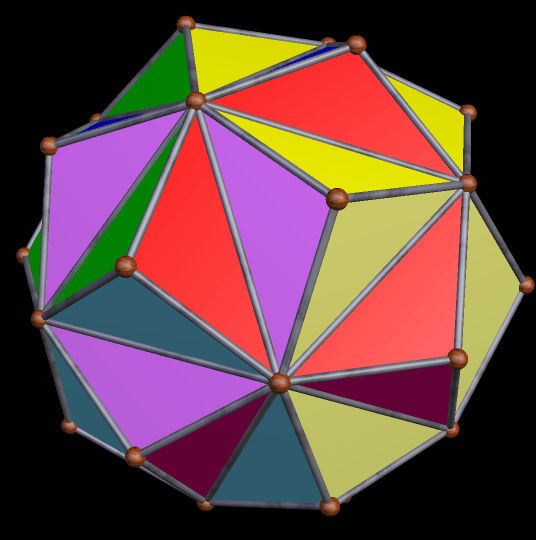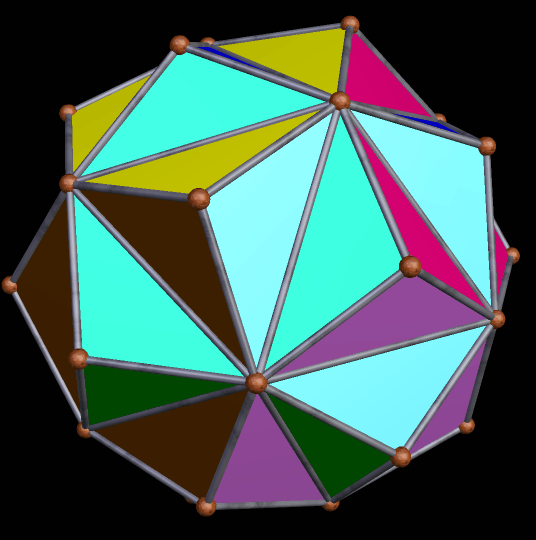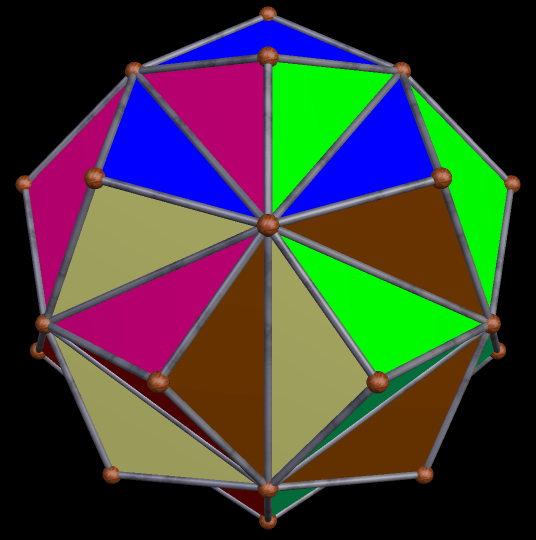
Selections from the Stellation-Series of the Icosidodecahedron
The icosidodecahedron has a long and interesting stellation-series, and you can see the whole thing using Stella 4d, the program I used to make the rotating .gifs here. Rather than keep the scale the same in each frame, I set the program to make the polyhedron as large as possible, while still fitting in the image-box. This creates the illusion that the polyhedra below are “breathing.”
The polyhedron above is the 20th stellation of the icosidodecahedron — the one that appeared as the sole image in the last post here, but with completely different colors. The next one shown is the 31st stellation.
The 55th stellation is immediately above, while the next one is the 69th.
The 84th stellation is immediately above, while the next one is the 89th.
The 106th stellation is immediately above, while the next one is the the 110th.
The 135th stellation is immediately above, while the next one, which is chiral, is the 157th.
Glimpses of the Invisible
Created using Stella 4d, available here, by multiple stellations of a black icosidodecahedron, rendered as a rotating figure, against a black background.
Stellating the Great Dodecahedron, by Twentieths, to Beethoven’s Ninth
In this video, the great dodecahedron is stellated, by twentieths, into the great stellated dodecahedron, while a selection from Ludwig van Beethoven’s Ninth Symphony plays. The images for this video were created using Stella 4d, a program you can try for yourself (free trial download available), right here: http://www.software3d.com/Stella.php.