This compound is the first I have seen which combines a Platonic solid (the blue octahedron) with a pyritohedral modification of a Platonic solid. Here’s what a pyritohedral dodecahedron looks like, by itself:
Stella 4d: Polyhedron Navigator was used to make these — software you can try right here: http://www.software3d.com/Stella.php.
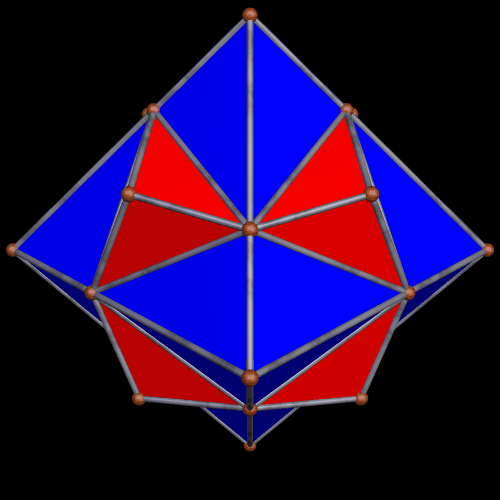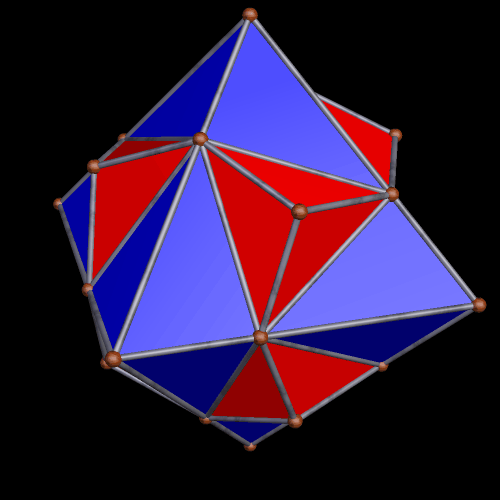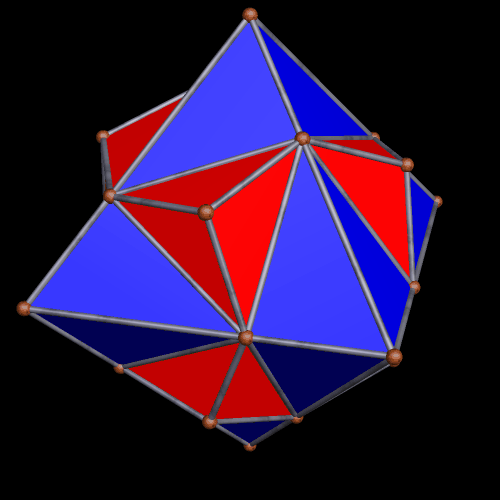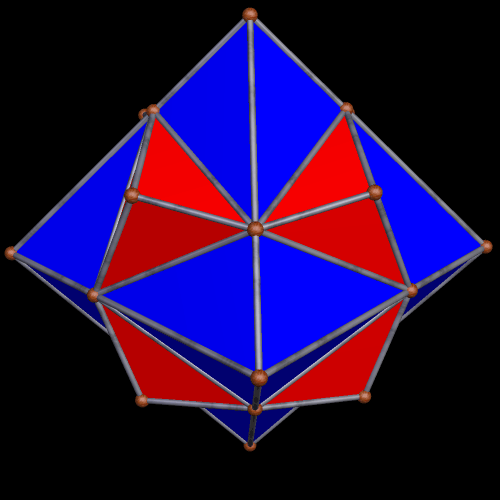
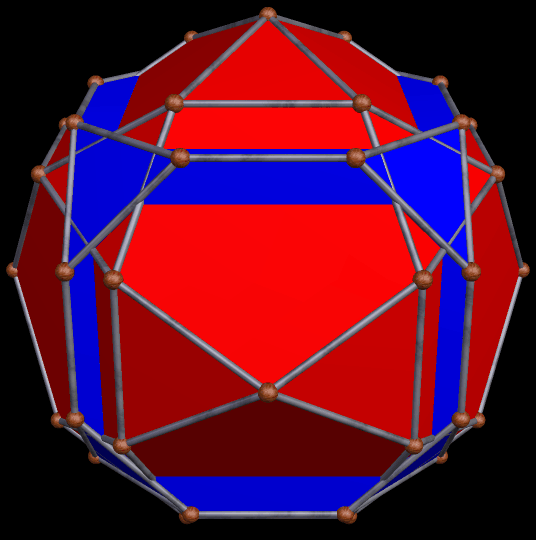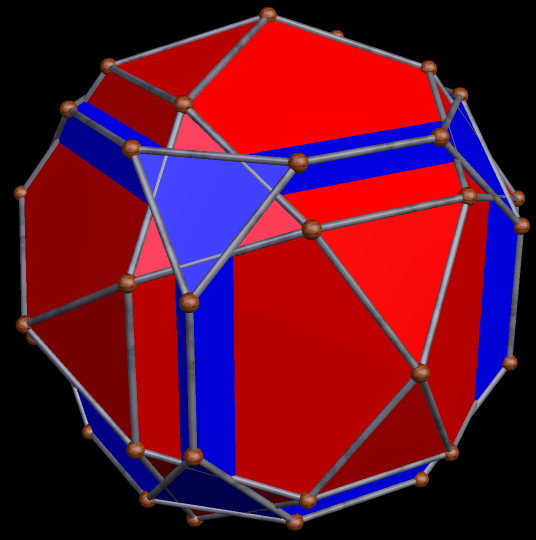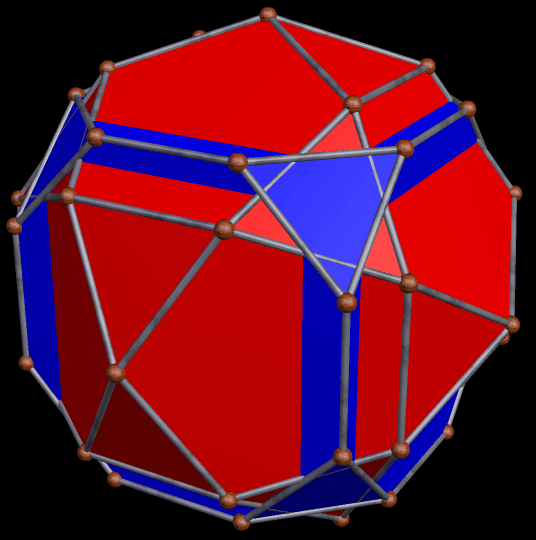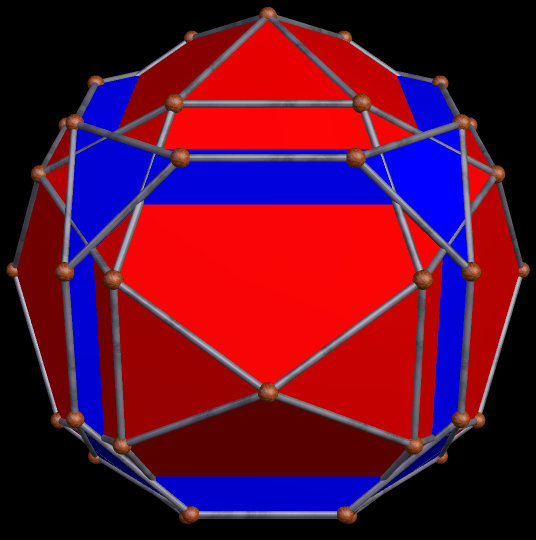
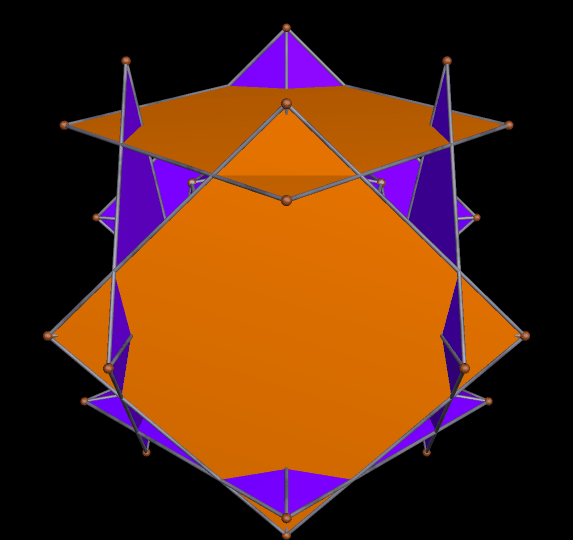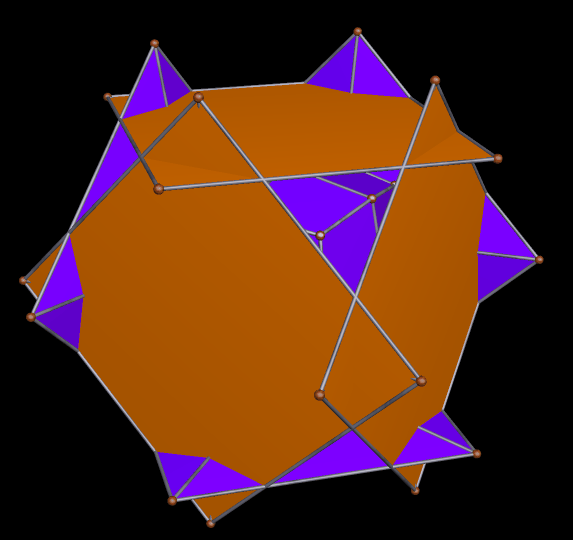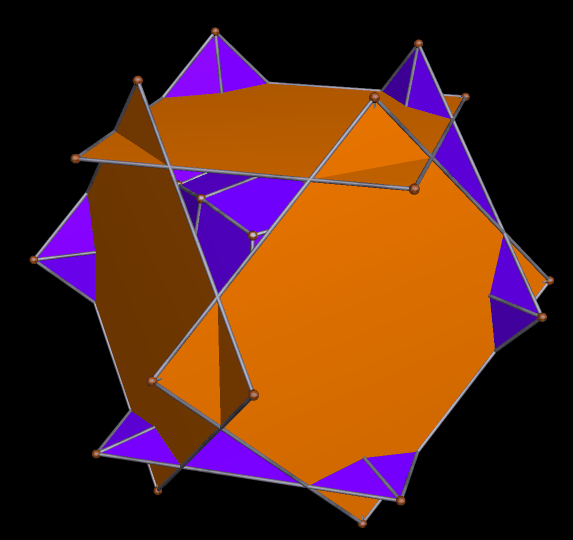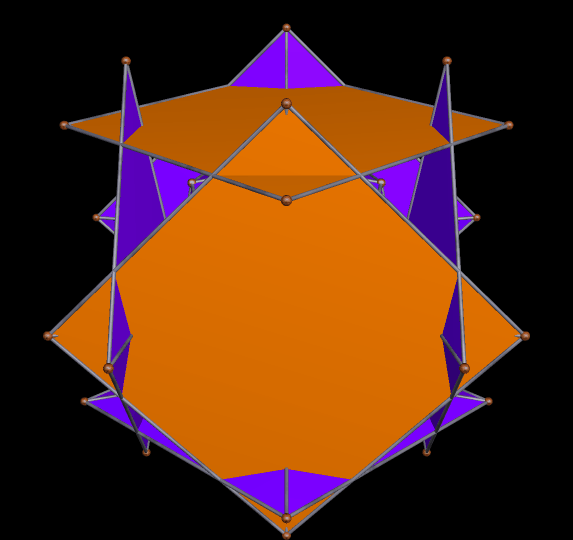
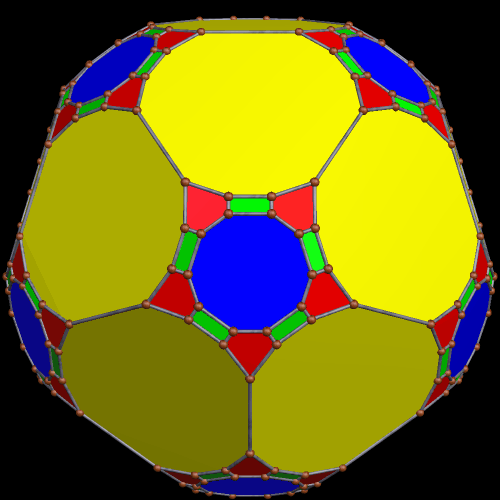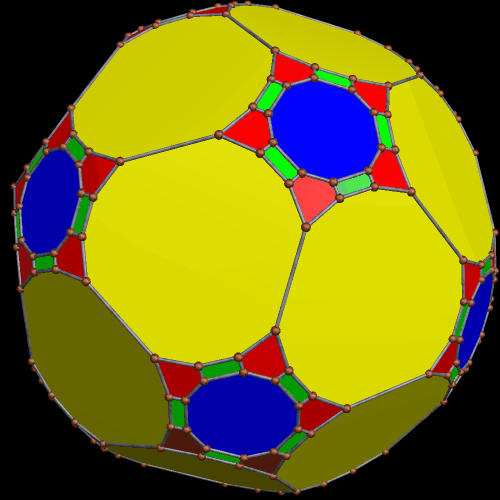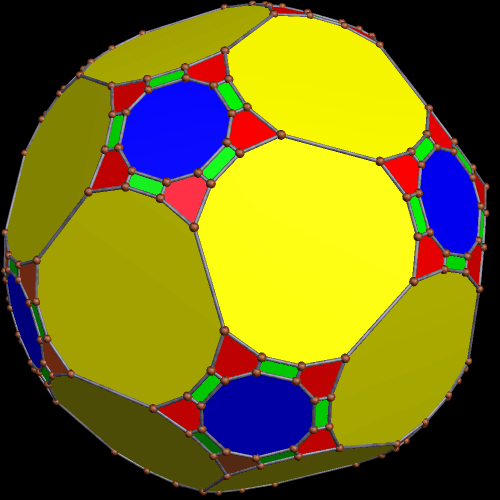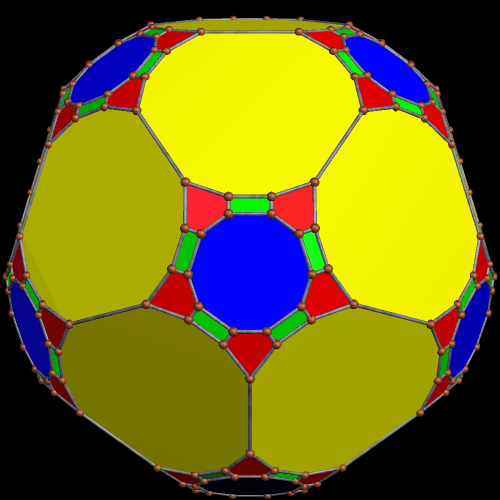
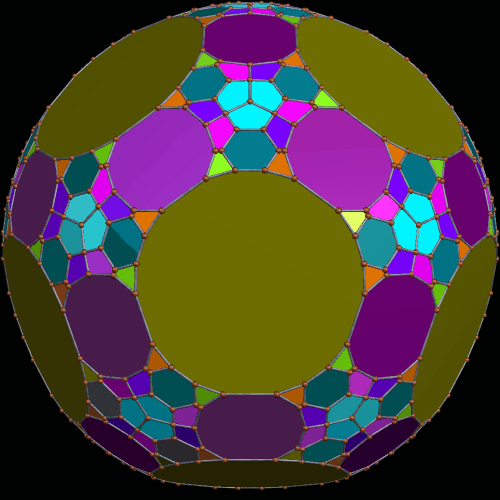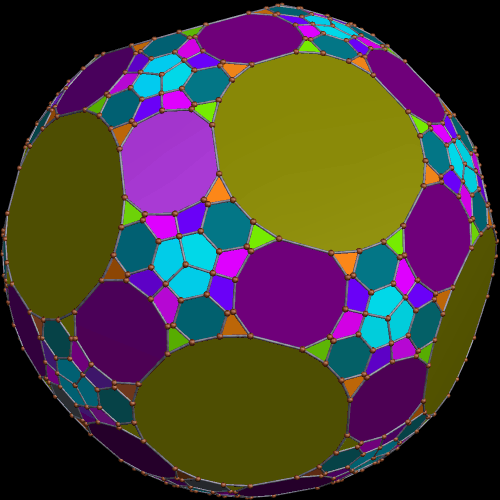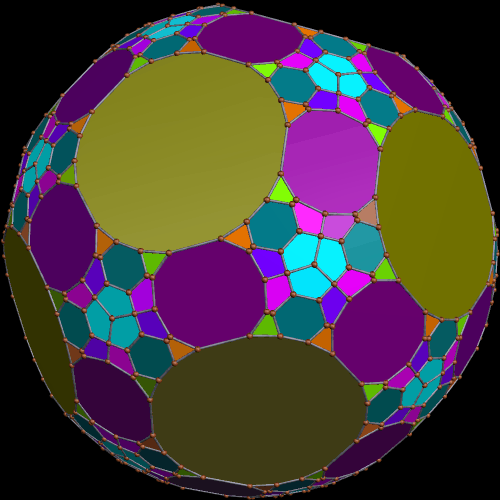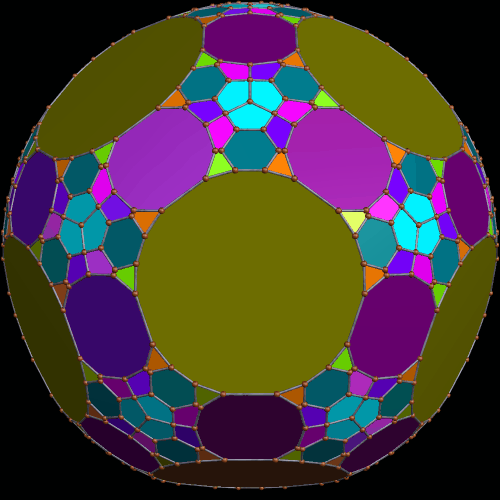
I stumbled upon this interesting hybrid of two well-known polyhedra, while simply playing around with Stella 4d, the software I use to make these rotating polyhedral images (you can try a free trial download of it here).
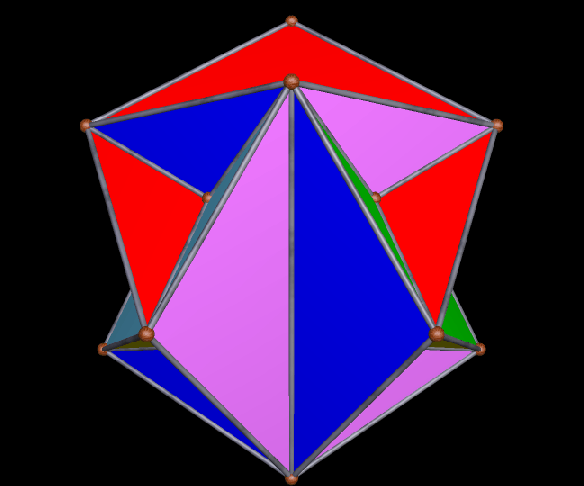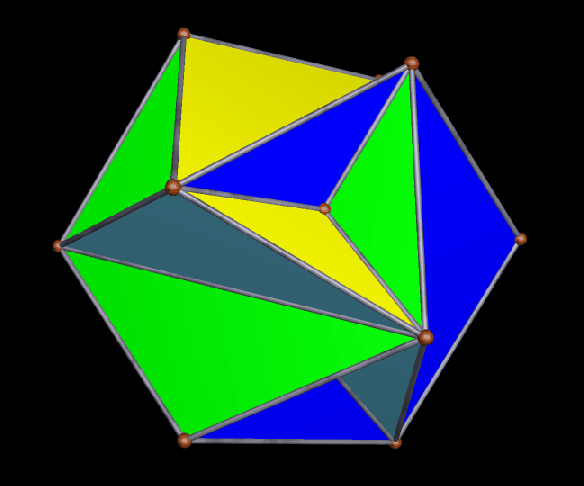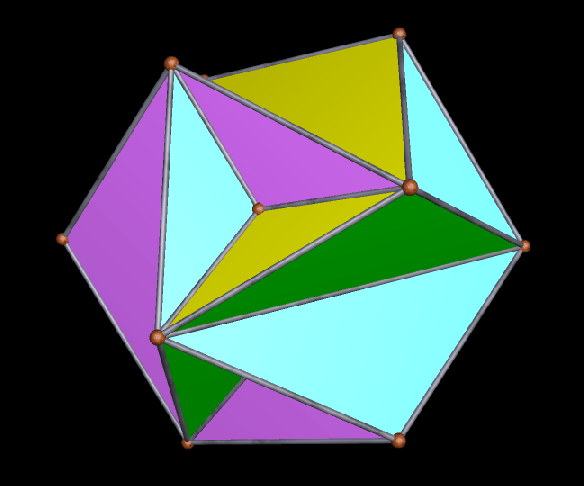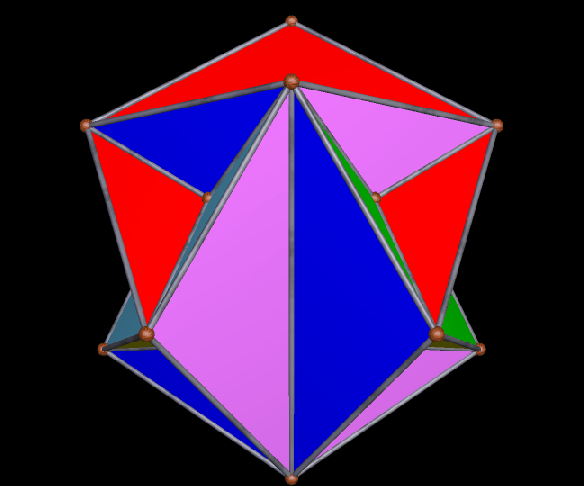
The faces of the above polyhedron are twelve modified regular pentagons, each with a triangular piece removed which contained one of the pentagon’s edges. Therefore, it would also be correct to refer to these modified pentagons as non-convex hexagons. These modified pentagons interpenetrate, so all that can be seen are triangular “facelets” — the parts of the faces which are not hidden inside the polyhedron. Each of these facelets is a golden gnomon (an obtuse, isosceles triangle with a base:leg ratio which is the golden ratio), and these golden gnomons come in two sizes. The larger ones were “inherited” from Jessen’s icosahedron, and there are twelve of them. The smaller golden gnomons, on the other hand, were “inherited” from the great dodecahedron, and are twenty-four in number, in eight sets of three. Like Jessen’s icosahedron itself, but unlike the great dodecahedron, this hybrid has pyritohedral symmetry.
For more information about Jessen’s icosahedron, please visit this site at Wolfram Mathworld. Also, here is an image of Jessen’s icosahedron, one of the two “parents” of the hybrid above.
While Jessen’s icosahedron is a relatively new discovery (Børge Jessen revealed it to the world in 1967), the hybrid’s other “parent,” the great dodecahedron, has been known for much longer; Louis Poinsot discovered it in 1809, according to this source. Here’s an image of the great dodecahedron.
As you can see, the smaller golden gnomons found in the hybrid above were “inherited” from the great dodecahedron, while the larger ones came from the six indented face-pairs found in Jessen’s icosahedron.
A well-known property of Jessen’s icosahedron is that it is “shaky,” unlike most polyhedra, which are rigid. A physical model of Jessen’s icosahedron, made from paper and tape, can, in fact, be collapsed to form an octahedron. While I suspect that a physical, paper-and-tape model of this newly-discovered hybrid polyhedron would share these properties (“shakiness,” and at least some degree of collapsibility), I have not (yet) tested this conjecture.
These two compounds, above and below, are duals. Also, in each of them, one polyhedron with icosidodecahedral symmetry is combined with a second polyhedron with cuboctahedral symmetry to form a compound with pyritohedral symmetry: the symmetry of a standard volleyball.
A program called Stella 4d was used to make these compounds, and create these images. It may be purchased, or tried for free, at this website.
I made these using Stella 4d, a computer program available at this website.
I made these using Stella 4d, available here.
Dodecahedra have icosahedral (also called icosidodecahedral) symmetry. In the figure above, this symmetry is changed to tetrahedral, by truncation of four vertices with positions corresponding to the vertices (or, instead, faces) of a tetrahedron. The interchangeability of vertices and faces for the tetrahedron is related to the fact that the tetrahedron is self-dual.
[Image created using Stella 4d, available here.]
Created with Stella 4d, available here.
Created with Stella 4d, available here.
Pyritohedral symmetry, seen by example both above and below, is most often described at the symmetry of a volleyball:
[Image of volleyball found here.]
To make the rotating polyhedral compound at the top, from an octahedron and an icosahedron, I simply combined these two polyhedra, using Stella 4d, which may be purchased (or tried for free) here.
In the process, I demonstrated that it is possible to combine a figure with octahedral (sometimes called cuboctahedral) symmetry, with a figure with icosahedral (sometimes called icosidodecahedral) symmetry, to produce a figure with pyritohedral symmetry.
Now I can continue with the rest of my day. No matter what happens, I’ll at least know I accomplished something.
I used Stella 4d to make the polyhedron above, and you can try this software for yourself here.
RobertLovesPi.net 