Zonohedra, Zonish Polyhedra, and Another Puzzle

Posted on 11 August 2016 by RobertLovesPi

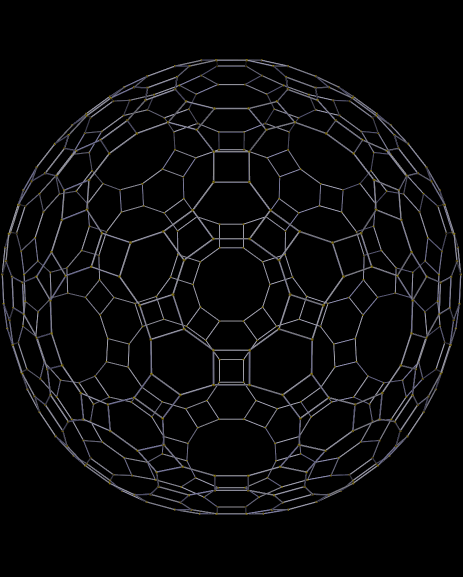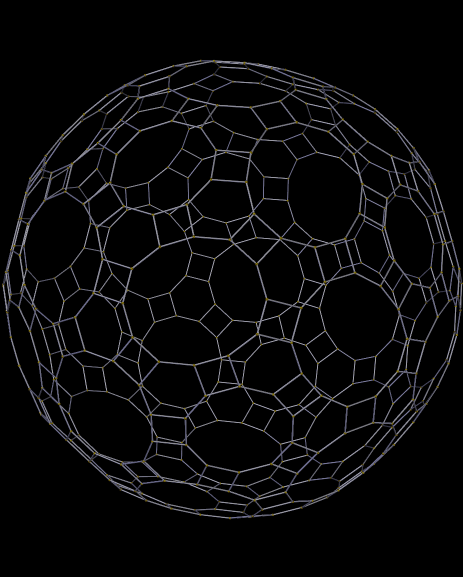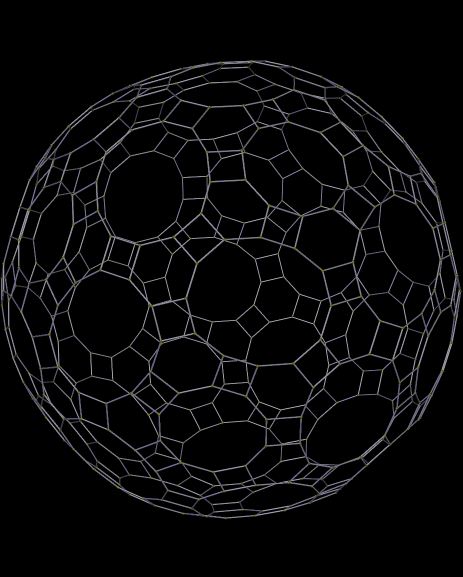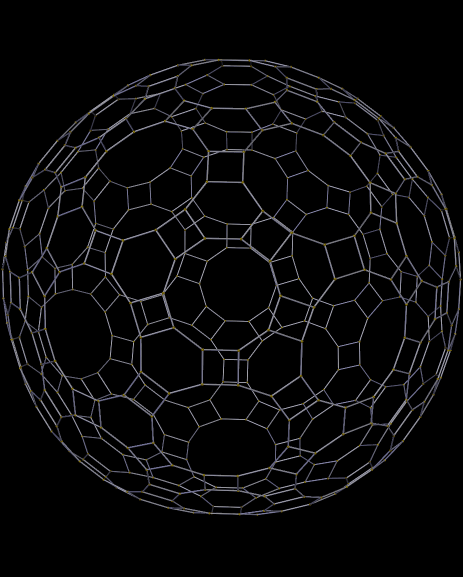
In a recent post, I showed many images of zonohedra, then challenged readers to figure out, from the images, what zonohedra are: polyhedra with only zonogons as faces. Zonogons, I then explained, are polygons with (A) even numbers of edges, and with opposite edges always (B) congruent and (C) parallel. Here is another collection of zonohedra. (Individual images may be enlarged with a click.)

Zonohedrified Trunc Cubocta faces are 552 rhombi

2256 rhombic faces Zonohedrified Trunc Cubocta

Zonohedrified Dual of Zonohedrified Triakisocta

The next set of polyhedra shown, below, are not true zonohedra (as all the ones above are), but merely “zonish polyhedra.” From examination of the pictures above and below, can you figure out the difference between zonohedra and zonish polyhedra?

When you are ready to see the solution to the puzzle, simply scroll down.

While zonohedra have only zonogons as faces, this restriction is “loosened” for zonish polyhedra. Such solids are formed by zonohedrifying non-zonohedral polyhedra, and letting at least some of the faces of the resulting polyhedra remain non-zonogonal. Zonish polyhedra are called “zonish” because many (usually most) of their faces are zonogons, but not all of them — in each case, some non-zonogonal polygons (such as triangles and/or pentagons, with their odd numbers of edges) do appear. Non-zonogonal polygons are not required to have odd numbers of edges, of course: simply having opposite edges be parallel, but of different lengths, is enough to prevent a polygon (such as a hexagon, octagon, or decagon) from being a zonogon.

~~~

Software credit: I used Stella 4d to make these images. This program may be tried for free at this website.

Some Zonohedra, and a Puzzle

Posted on 4 August 2016 by RobertLovesPi

Every zonohedron is a polyhedron, but not all polyhedra are zonohedra. Examples of zonohedra appear below. If you don’t already know what zonohedra are, can you figure out the definition from the examples shown, before reading the definition below the pictures?

Zonohedrified Stellated Snub Cube 2346 faces

Zonohedrified Stellated Snub Cube 1770 faces

26522-faced Zonohedrified Augmented Poly

Answer below (scroll down a bit):

Zonohedra are polyhedra with only zonogons as faces. A zonogon is a polygon with an even number of sides, and also with opposite sides congruent and parallel.

Software credit: I used Stella 4d to make these virtual, rotating zonohedra. This program may be tried for free at http://www.software3d.com/Stella.php.

Three Different Views of a 962-Faced Zonohedron

Posted on 4 March 2016 by RobertLovesPi

This zonohedron contains faces which are regular decagons (12 of them), equilateral octagons (30, all of the same type), equilateral hexagons (380 of them, of 7 types, with one of these 7 types, of which there are 20, being regular), squares (60), and non-square rhombi (480 of 8 types, counting reflections as separate types). With each polygon-type, including the reflections, given a different color, this zonohedron looks like this.

If reflected face-types are not counted as separate types, then the coloring-by-face-type uses four fewer colors, and looks like this:

Another view simply colors faces by numbers of sides, and is shown below. Each of these rotating images was created with Stella 4d, a program you may buy, or try for free, at http://www.software3d.com/Stella.php.

A Zonish Polyhedron with 522 Faces, Together with Its 920-Faced Dual

Posted on 18 January 2016 by RobertLovesPi

zonol

The polyhedron above is a 522-faced zonish polyhedron, which resembles, but is not identical to, a zonohedron. True zonohedra are recognizable as that type of polyhedron by their exclusively zonogonal faces. Zonogons are polygons with even numbers of sites, and with opposite sides both congruent and parallel. If you examine the polyhedron above carefully, you’ll find it does not follow these rules. Stella 4d, the polyhedral-manipulation software I use to make these images, allows one to create either a true zonohedron, or a mere “zonish” polyhedron, as the user chooses, starting from another polyhedron (which may, itself, be zonish, a true zonohedron, or neither).

The next polyhedron is the dual of the polyhedron above. This dual has 920 faces. The duals of both zonohedra and zonish polyhedra have a distincive appearance, but, to my knowledge, no one has yet given either set of polyhedra a single-word name. In my opinion, such names are both needed, and deserved.

zono 920 faces dual of the one that had 522 faces

If you would like to try Stella 4d for yourself, there is a free trial download available at http://www.software3d.com/Stella.php.

A Zonohedron with 3540 Faces, Together with Its Dual

Posted on 7 November 2015 by RobertLovesPi

Zonohedra are polyhedra made completely of faces which are zonogons. A zonogon is a polygon which:

Has an even number of sides,
Has opposite sides congruent, and
Has opposite sides parallel.

Parallelograms are the simplest zonogons.

Here is the dual of the zonohedron above; it has 3542 faces. Although zonohedra-duals do have distinctive appearances, they do not, as a class, have a name of their own, to the best of my knowledge. They are definitely not zonohedra, themselves.

Both of these polyhedra were created with Stella 4d, software you may try for yourself, right here.

A Twice-Zonohedrified Dodecahedron, Together with Its Dual

Posted on 25 October 2015 by RobertLovesPi

This polyhedron was created by performing vertex-based zonohedrifications of a dodecahedron — twice. The first zonohedrification produced a rhombic enneacontahedron, various version of which I have blogged many times before, but performing a second zonohedrification of the same type was a new experiment. It has 1230 faces, 1532 vertices, and 2760 edges. All of its edges have equal length. I created the models in this post using Stella 4d, a program you can buy, or try for free, right here.

Here is the dual of this zonohedron, which has 1532 faces, 1230 vertices, and 2760 edges. This “flipping” of the numbers of faces and vertices, with the number of edges staying the same, always happens with dual polyhedra. I do not know of a name for the class of polyhedra made of zonohedron-duals, but, if any reader of this post knows of one, please leave this name in a comment.

Zonohedron Based On the Edges and Vertices of a Great Rhombcuboctahedron

Image

Zonohedron Based On the Edges and Vertices of a Great Rhombcuboctahedron

This polyhedral monster has 578 faces of 26 types. In the image above, hexagons of any type are red, rhombi of any type (including squares) are yellow, and the blue faces are octagons. If each face-type is given a different color, though, this zonohedron looks like this:

Another coloring-scheme — the best one, in my opinion — is like the first one here, except that regular hexagons are given their own color (purple), and squares are given their own as well (black):

All three images were created with Stella 4d, software available at http://www.software3d.com/Stella.php.

A Fifty-Faced, Zonohedrified Form of the Truncated Octahedron

Image

A Zonohedrified Form of the Truncated Octahedron

This zonohedron has fifty faces:

6 regular octagons
8 regular hexagons
24 squares
12 equilateral octagons, the only irregular polygons needed as faces of this polyhedron

(Image created with Stella 4d — software you can try yourself at http://www.software3d.com/Stella.php.)

A Wire-Frame Zonohedron Based On the Faces, Edges, and Vertices of an Icosahedron

Image

A Wire-Frame Zonohedron Based On the Faces, Edges, and Vertices of an Icosahedron

This is the shape of the largest zonohedron one can make with red, yellow and blue Zome (see http://www.zometool.com for more on that product for 3-d real-world polyhedron modeling). This image was made using Stella 4d, which you can find at http://www.software3d.com/stella.php.