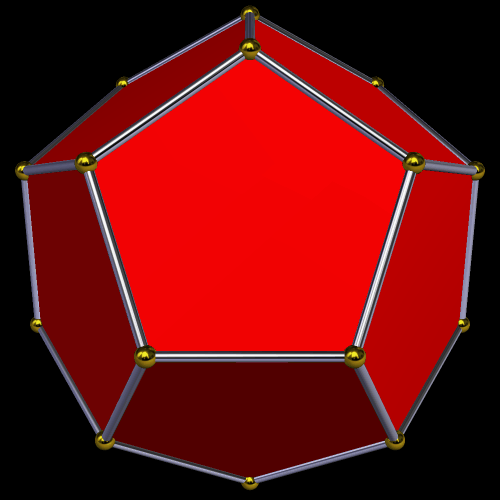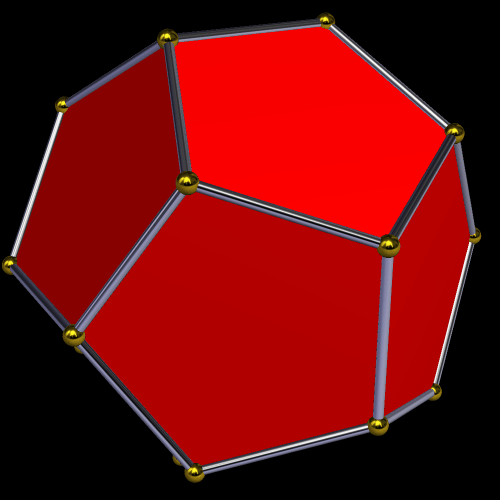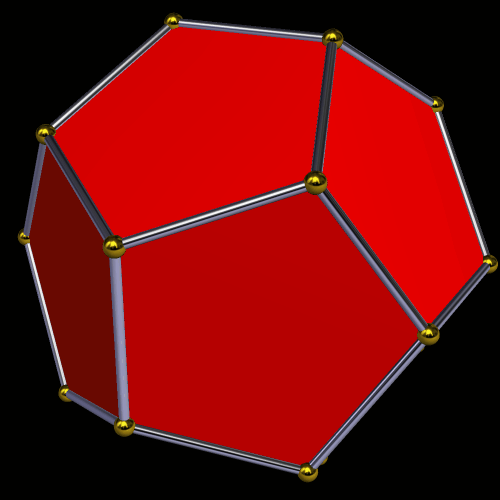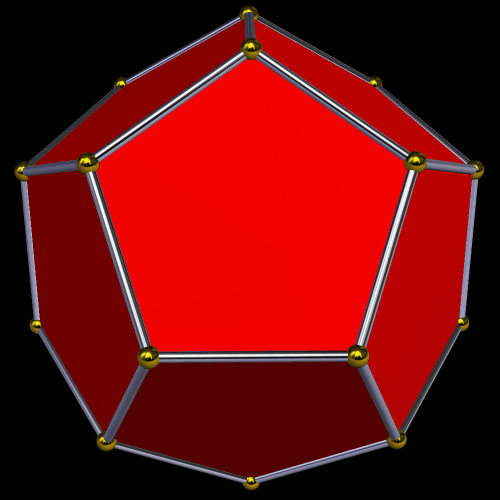
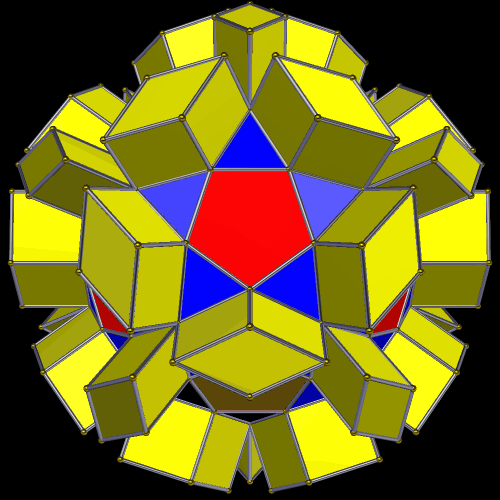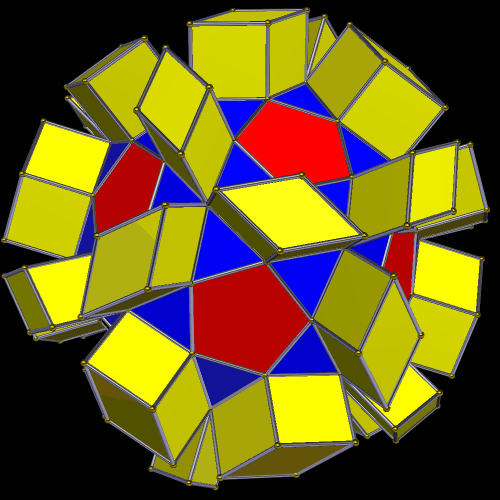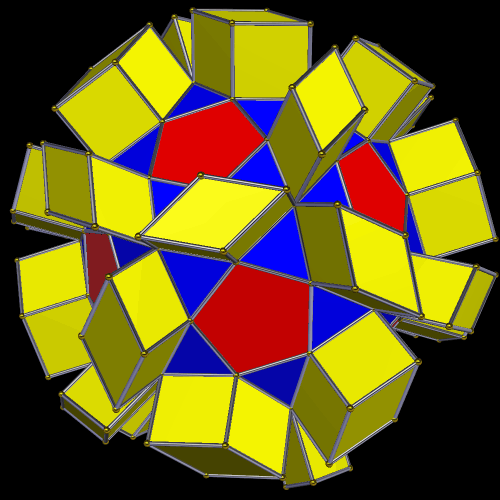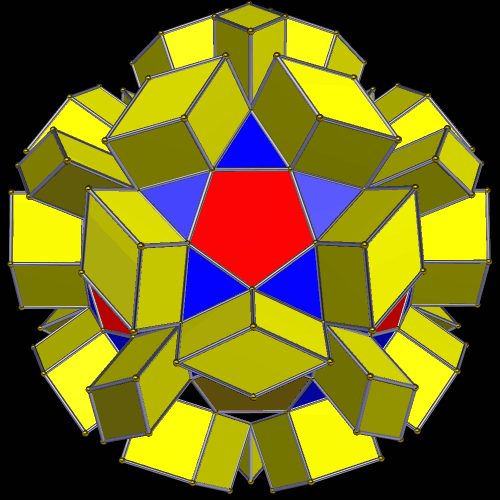
Some Concentric, All-Blue Zome Polyhedra

Posted on 4 June 2024 by RobertLovesPi

In the center of this figure is a regular dodecahedron, but it’s hard to spot. It is then stellated to form a small stellated dodecahedron. Next, its outer vertices are joined by new edges: those of an icosahedron. This also results in the formation of a great dodecahedron. Finally, the icosahedron is stellated to form the great stellated dodecahedron. To take this further, one could connect the outer vertices with new edges: those of a dodecahedron. The entire process can begin again, then, and this could continue without limit, filling all of space.

Here’s a closer view of the interior:

Zometools may be purchased at http://www.zometool.com.

A Near-Miss to the Johnson Solids, Which I’m Naming the Ditrated Dodecahedron, Part Two

Posted on 16 May 2024 by RobertLovesPi

(If you haven’t yet read part one, I strongly recommend reading it first.)

With the help of Tadeusz Dorozinski and Hunter Hughes, my new near-miss (the discovery of which was described here) is now better-understood. The isosceles triangles’ shared bases are about 5% longer than the solid’s other edges, which is within the range generally allowed for near-misses. I have not yet found any mention of this discovery before I found it yesterday, while playing with a broken, plastic d12.

Here is a net for this solid:

Also, here is its dual, as well as a net for the dual.

These images were generated using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.

[Update: I am now convinced that I am not the first person to find this near-miss. On the other hand, I don’t know who that first person actually is.]

A Near-Miss to the Johnson Solids, Which I’m Naming the Ditrated Dodecahedron, Part One

Posted on 15 May 2024 by RobertLovesPi

I had a strange mishap recently with a member of my large collection of polyhedral dice. This hollow d12 fell apart, into two panels of six pentagons each.

I held them together at vertices, rotating one of the panels slightly.

Those gaps aren’t rhombi, because their four vertices are noncoplanar. Instead of rhombi, therefore, I’m filling the gaps with pairs of isosceles triangles. I’m going to request help from experts to find the edge length ratio for these isosceles triangles, but I know it isn’t 1:1, since all 92 of the Johnson solids have been found.

I think this particular near-miss may have been found and posted before in a Facebook group devoted to polyhedra, as a magnetic ball-and-stick model, but I don’t think it was named at that time. The name “ditrated dodecahedron” is derived from “tetrated dodecahedron,” which you can read about right here. The tetrated dodecahedron has four panels of pentagons rotated away from the center, while the ditrated dodecahedron has only two panels. The latter’s faces are twelve regular pentagons, and ten isosceles triangles.

I’m going to post this in that Facebook group where I think this near-miss to the Johnson solids may have been seen before, in an effort to spread the discovery-credit around anywhere it has been earned. I’d also like to have a Stella 4d model of this solid, and for that, again, I need the help of experts. Once I know more about this near-miss, I’ll post part two. [Update: part two is right here.]

Repeated Augmentations of a Dodecahedron With More and More Dodecahedra

Posted on 20 April 2022 by RobertLovesPi

Here’s a single dodecahedron.

A new “cluster polyhedron” can be made by augmenting each pentagonal face with another dodecahedron.

If you can do it once, you can do it again, augmenting each pentagon with a new dodecahedron.

Once more.

I made these polyhedral clusters using Stella 4d: Polyhedron Navigator, which you can try for free at http://www.software3d.com/Stella.php.

Binary Dodecahedra

Posted on 16 August 2021 by RobertLovesPi

I made this .gif, of two dodecahedra orbiting a common center of mass, using a program called Stella 4d: Polyhedron Navigator. This program may be tried for free at http://www.software3d.com/Stella.php.

A Polyhedral Journey, Starting with the Compound of Five Dodecahedra

Posted on 30 May 2021 by RobertLovesPi

This is the compound of five dodecahedra, a shape which is included in the built-in polyhedral library of Stella 4d, a program you can try for yourself, free, right here.

I wanted to see what I could make, starting from this compound. My first modification to it was to create its convex hull, which is shown below.

The next move was to use Stella‘s “Try to Make Faces Regular” function, which produced this:

Next, I augmented this figure’s thirty yellow rhombi with prisms.

I then created the convex hull of this augmented polyhedron.

Next, I used the “Try to Make Faces Regular” function again, producing a solid that looks, to me, like a hybrid of the rhombicosidodecahedron and the rhombic triacontahedron.

This polyhedron has yellow faces that are almost squares. Careful inspection reveals that they are actually isosceles trapezoids. The next thing I did was to augment each of these trapezoids with a tall prism.

The next step was to, again, create the convex hull.

That was the end of this polyhedral journey, but I am confident there will be others.

Spectral Dodecahedra

Posted on 2 February 2020 by RobertLovesPi

Stella 4d: Polyhedron Navigator has a “put models on vertices” function which I used to build this cluster of 101 dodecahedra. If you’d like to try this software for yourself, there is a free trial download available at http://www.software3d.com/Stella.php.

A Dozen Dodecahedra, Surrounding an Icosahedron

Posted on 22 January 2020 by RobertLovesPi

I made these virtual models using Stella 4d: Polyhedron Navigator. If you’d like to try this program for yourself — free — the website to visit is http://www.software3d.com/Stella.php.