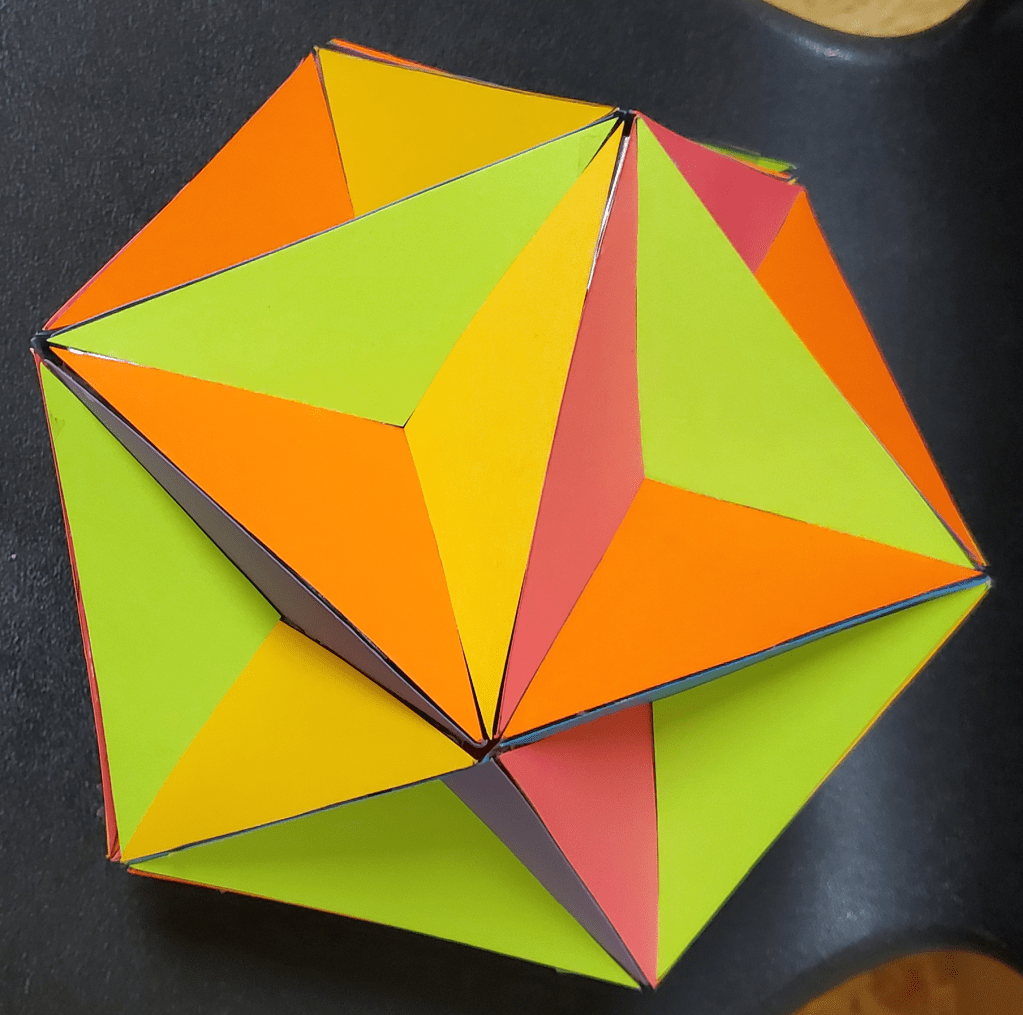Tag Archives: dodecahedron

Two Views of a Paper Model of the Great Dodecahedron

Posted on by
Reply

The obtuse triangles here are golden gnomons, which are isosceles triangles with vertex angles of 108 degrees, as well as base-to-leg ratios which are golden. These triangles are facelets; the actual, much larger faces are the regular pentagons of which the golden gnomons are parts. In this model, all facelets which are part of the same (or parallel) faces are all one color, with six colors of paper used, in all, for this non-convex, twelve-faced, regular polyhedron, which is one of the Kepler-Poinsot solids.

Much of each face is hidden from view in this polyhedron’s interior — or rather, this is the case for the mathematical construct called the great dodecahedron. This physical model, on the other hand, is hollow on the inside. One is made only of ideas, while the other is made of atoms.

No computer programs were involved in the construction of this model. It was made using compass, straight edge, scissors, card stock, pencils, and tape.

Five Views of the Compound of the Truncated Dodecahedron and the Truncated Icosahedron

Posted on by
1

When I let Stella 4d (a program you can try for free right here) choose the colors of this compound, here’s what I was shown.

Next, I chose “color as a compound.”

For the third view, I chose “color by face type,” which yields four colors instead of two.

The fourth model shown here shows this compound in “rainbow color mode.”

Finally, the fifth coloring-scheme I tried was “color by face, unless parallel.”

Which one do you like best? My favorite is the third one shown.

Some Concentric, All-Blue Zome Polyhedra

Posted on by
Reply

In the center of this figure is a regular dodecahedron, but it’s hard to spot. It is then stellated to form a small stellated dodecahedron. Next, its outer vertices are joined by new edges: those of an icosahedron. This also results in the formation of a great dodecahedron. Finally, the icosahedron is stellated to form the great stellated dodecahedron. To take this further, one could connect the outer vertices with new edges: those of a dodecahedron. The entire process can begin again, then, and this could continue without limit, filling all of space.

Here’s a closer view of the interior:

Zometools may be purchased at http://www.zometool.com.

A Near-Miss to the Johnson Solids, Which I’m Naming the Ditrated Dodecahedron, Part Two

Posted on by
4

(If you haven’t yet read part one, I strongly recommend reading it first.)

With the help of Tadeusz Dorozinski and Hunter Hughes, my new near-miss (the discovery of which was described here) is now better-understood. The isosceles triangles’ shared bases are about 5% longer than the solid’s other edges, which is within the range generally allowed for near-misses. I have not yet found any mention of this discovery before I found it yesterday, while playing with a broken, plastic d12.

Here is a net for this solid:

Also, here is its dual, as well as a net for the dual.

These images were generated using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.

[Update: I am now convinced that I am not the first person to find this near-miss. On the other hand, I don’t know who that first person actually is.]

A Near-Miss to the Johnson Solids, Which I’m Naming the Ditrated Dodecahedron, Part One

Posted on by
1

I had a strange mishap recently with a member of my large collection of polyhedral dice. This hollow d12 fell apart, into two panels of six pentagons each.

I held them together at vertices, rotating one of the panels slightly.

Those gaps aren’t rhombi, because their four vertices are noncoplanar. Instead of rhombi, therefore, I’m filling the gaps with pairs of isosceles triangles. I’m going to request help from experts to find the edge length ratio for these isosceles triangles, but I know it isn’t 1:1, since all 92 of the Johnson solids have been found.

I think this particular near-miss may have been found and posted before in a Facebook group devoted to polyhedra, as a magnetic ball-and-stick model, but I don’t think it was named at that time. The name “ditrated dodecahedron” is derived from “tetrated dodecahedron,” which you can read about right here. The tetrated dodecahedron has four panels of pentagons rotated away from the center, while the ditrated dodecahedron has only two panels. The latter’s faces are twelve regular pentagons, and ten isosceles triangles.

I’m going to post this in that Facebook group where I think this near-miss to the Johnson solids may have been seen before, in an effort to spread the discovery-credit around anywhere it has been earned. I’d also like to have a Stella 4d model of this solid, and for that, again, I need the help of experts. Once I know more about this near-miss, I’ll post part two. [Update: part two is right here.]

Two Views of the Compound of the Great Dodecahedron and the Platonic Dodecahedron

Posted on by
2

I made this using Stella 4d, which you can try for free right here. In the image above, the two components of this compound are given separate colors. In the second picture, below, the coloring is per face, except for parallel faces, which have the same color.

A Dodecahedron, Encased By Stars

Posted on by
4

I made this using Stella 4d, which you can try for free right here.

The Four Gas Giants on the Faces of a Dodecahedron

Posted on by
Reply

These images of Jupiter, Saturn, Uranus, and Neptune were all acquired by NASA. I placed them on this polyhedron, and created this rotating .gif, using Stella 4d, which you can try for free at this website.

Two Views of a Faceted Dodecahedron

Posted on by
1

This is one of many possible facetings of the dodecahedron. It’s colored by face type above, and is shown in “rainbow color mode” below. I made both rotating images using Stella 4d, which you can try for free at this website.

A Zonish Dodecahedron

Posted on by
1

This zonish polyhedron has 162 faces, and is based on the faces and the vertices of a dodecahedron. I made it using Stella 4d, which you can try for free at this website.