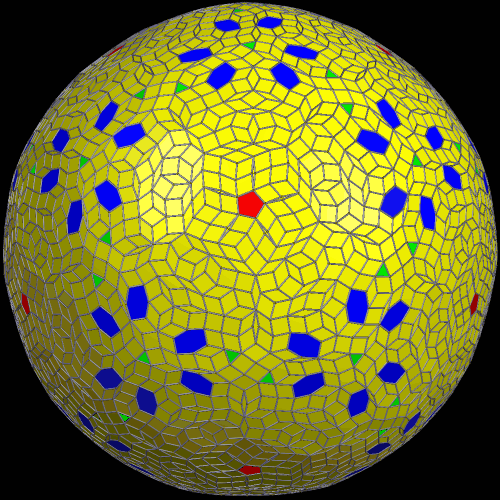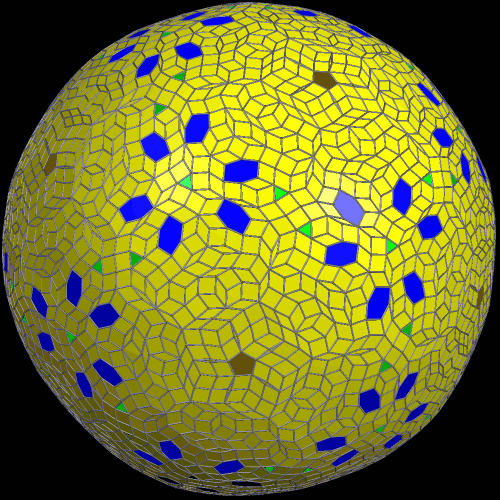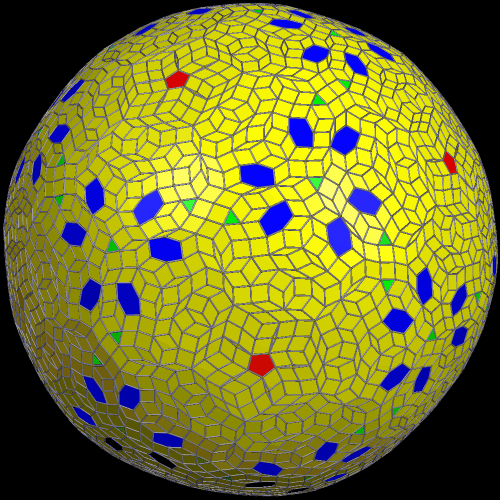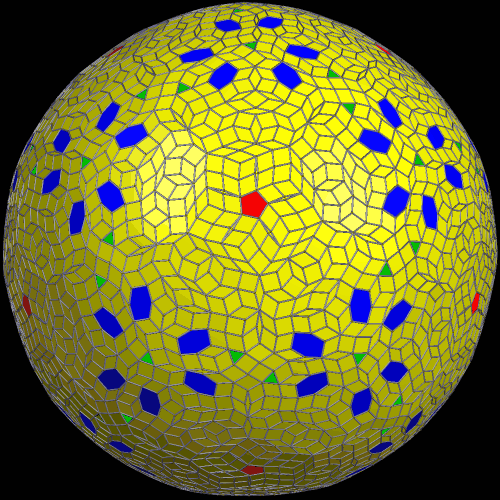
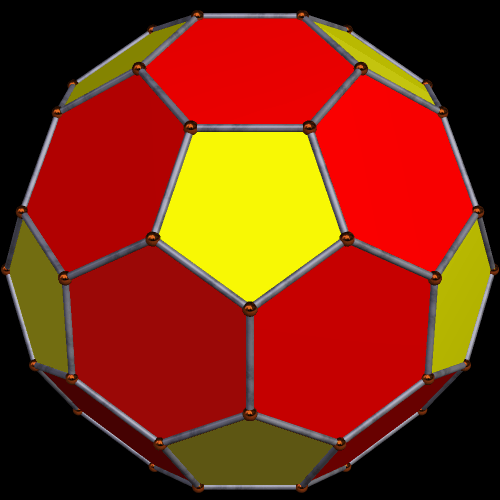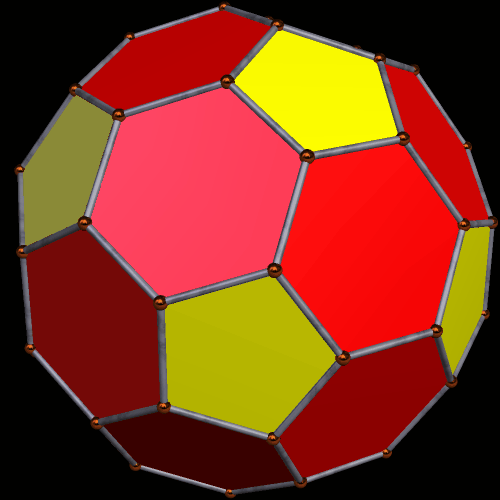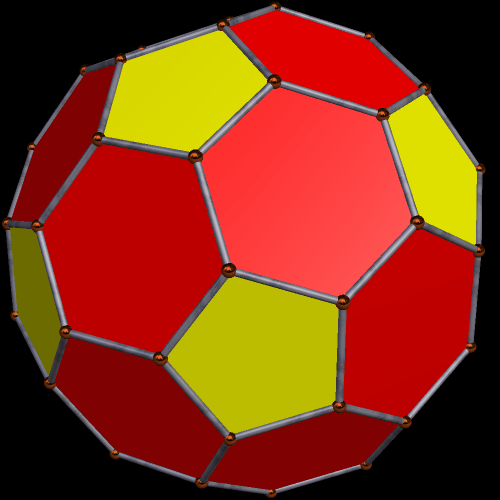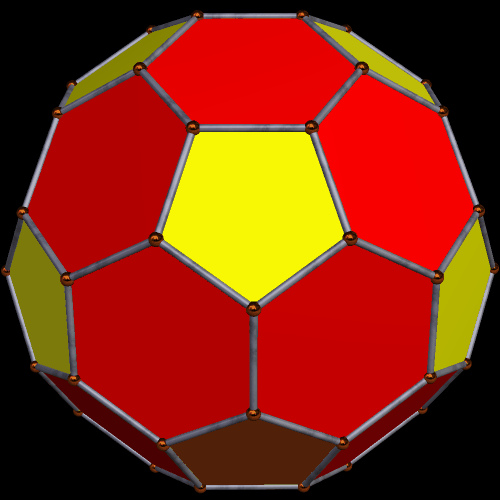
Give the polyhedron below a quick glance. Can you name it?

Since there are twelve regular pentagons, and a bunch of hexagons, it looks like a soccer ball. The shape of the most widely-used soccer ball is a (rounded) truncated icosahedron. Therefore, you can be forgiven if you thought this thing was a truncated icosahedron. Take a close look at those hexagons, though. Can you see that they are not regular?

Contrast the solid above to the shape below, which is a real truncated icosahedron.

The hexagons in this second image are regular, but that isn’t the only difference between the two. Examine the vertices of solid #2. At each vertex, one pentagon meets two hexagons. Scroll up and take another look at solid #1, and you can easily find vertices there which also have two hexagons meeting a pentagon — but not all of the vertices are like that. Some of the vertices have three hexagons meeting there, without any pentagons at all. This allows more hexagons into the mix, while the number of pentagons stays steady, at twelve, in both polyhedra.

There are also other differences. For example, the “fake” truncated icosahedron has eighty vertices, while the real one has sixty. The first solid is actually the dual of a frequency-2 geodesic sphere. It’s not an Archimedean solid at all. It is, in chemistry, a fullerene; in fact, both shapes are fullerenes. One is the well known C₆₀ molecule, while the other is a less familiar fullerene with the formula C₈₀. 

Both of these polyhedra can be built using Zometools (available for sale at http://www.zometool.com). The truncated icosahedron requires sixty Zomeballs, and is made of all blue struts. The geodesic-sphere dual takes eighty Zomeballs, and is made of blue and red struts.

Both images here were made with a computer program called Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.