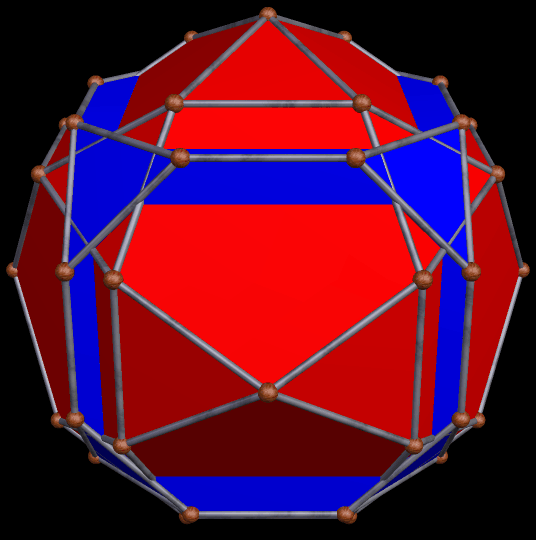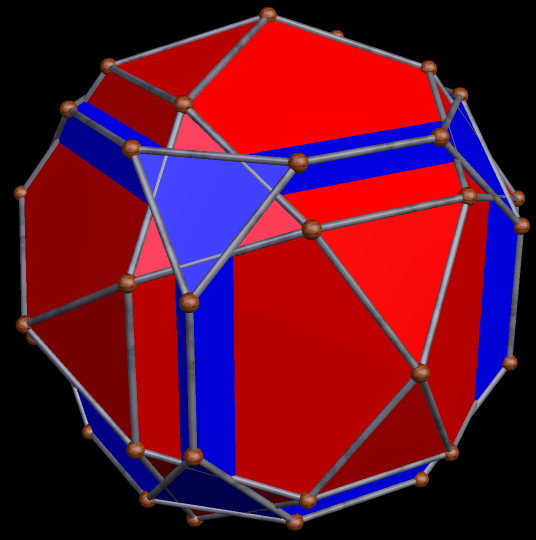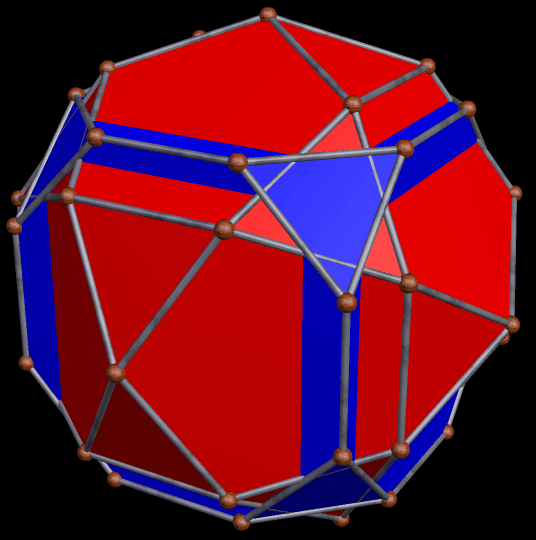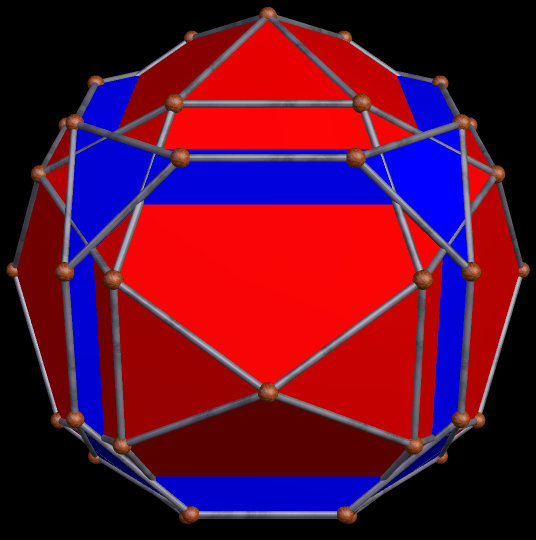
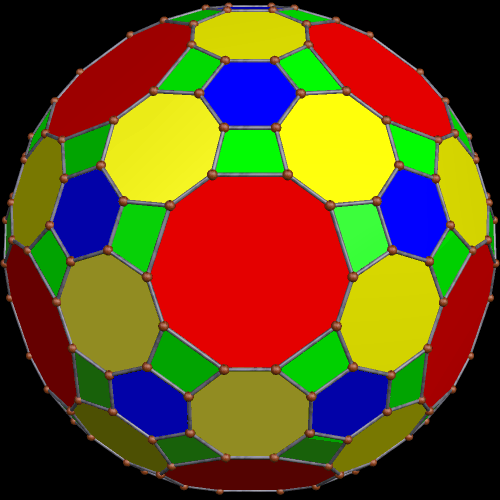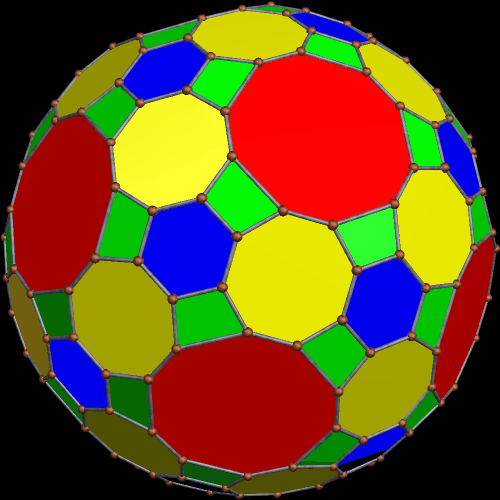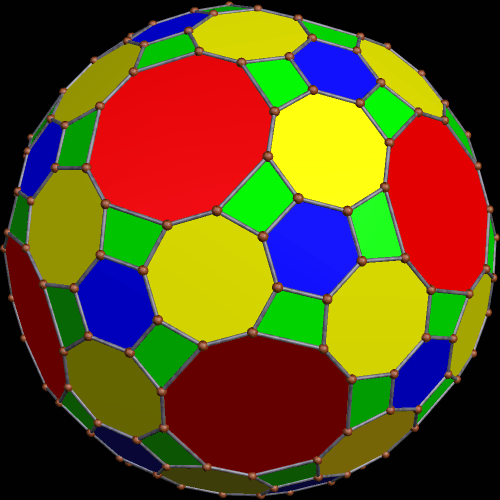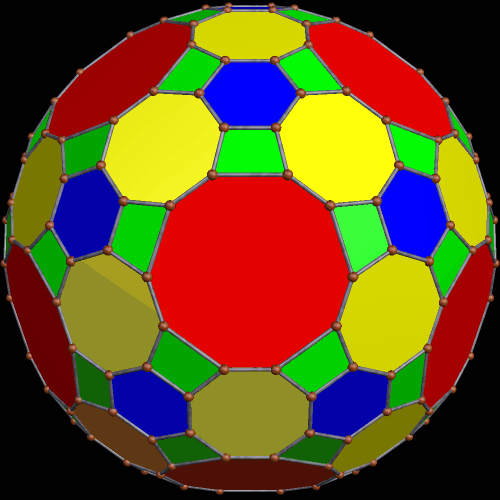
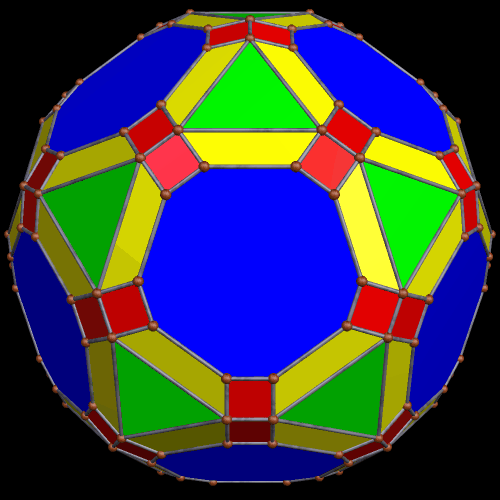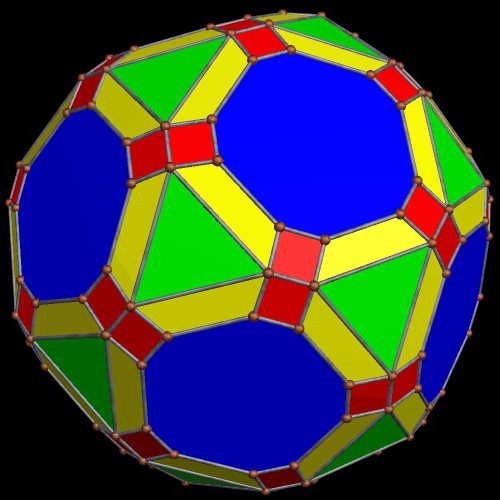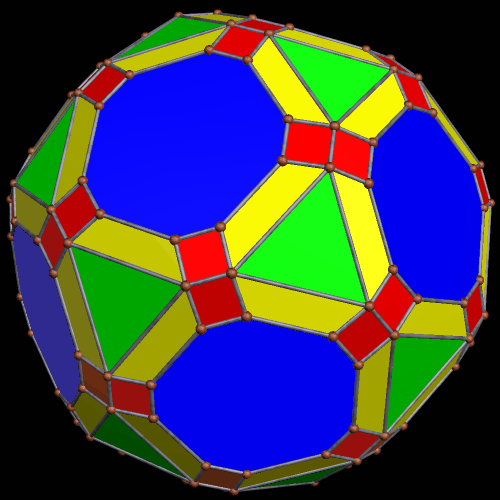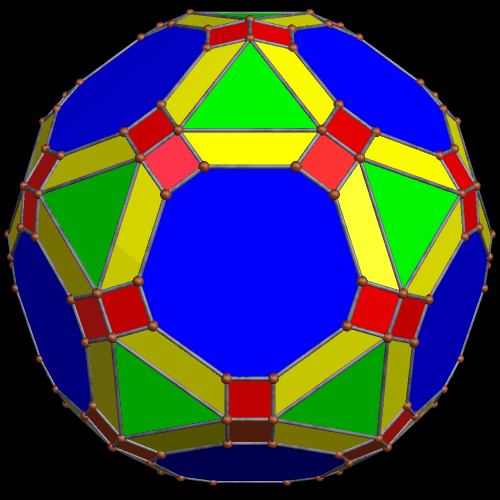
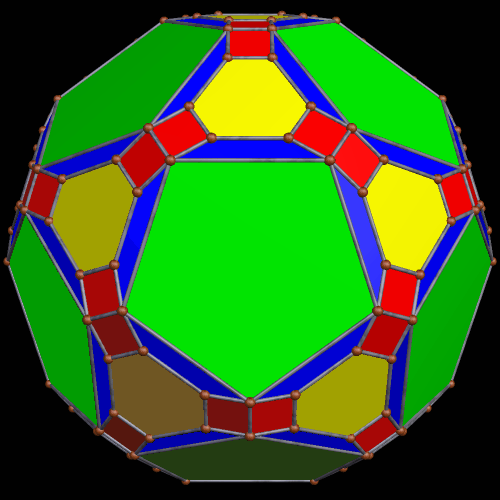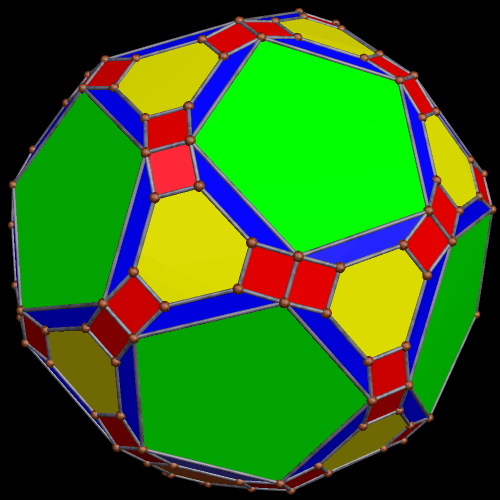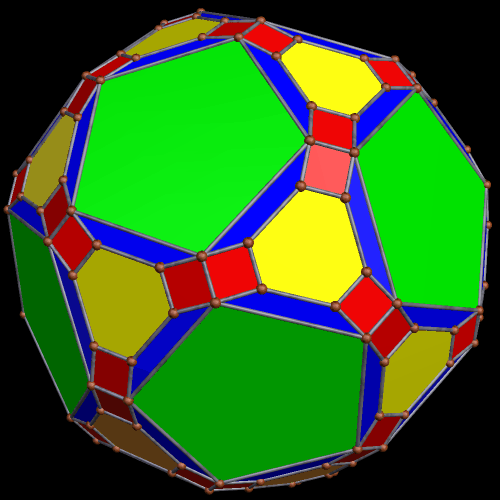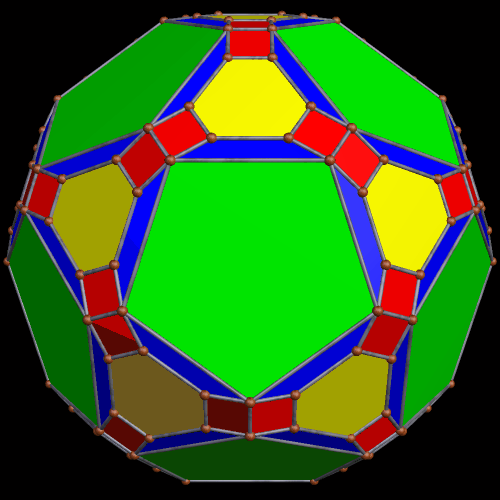
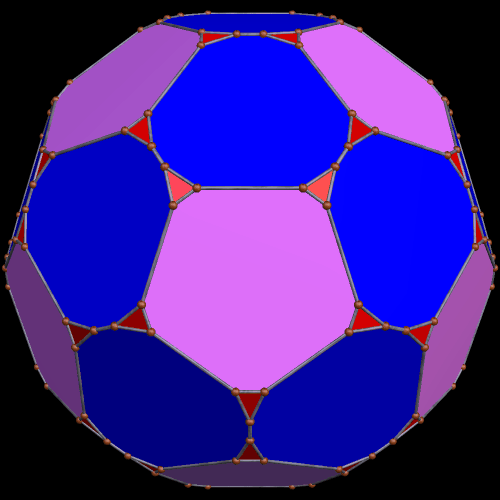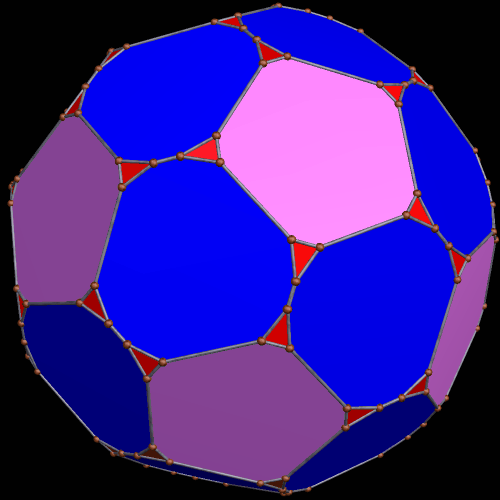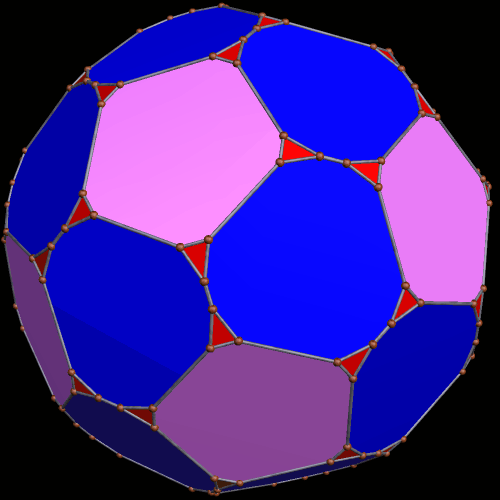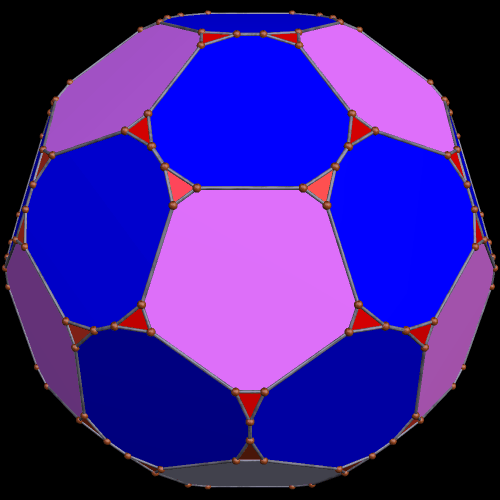
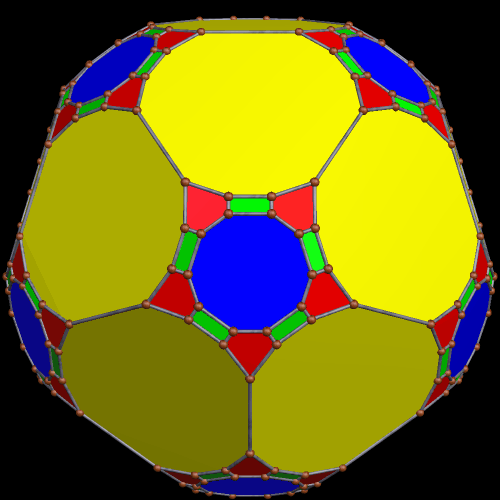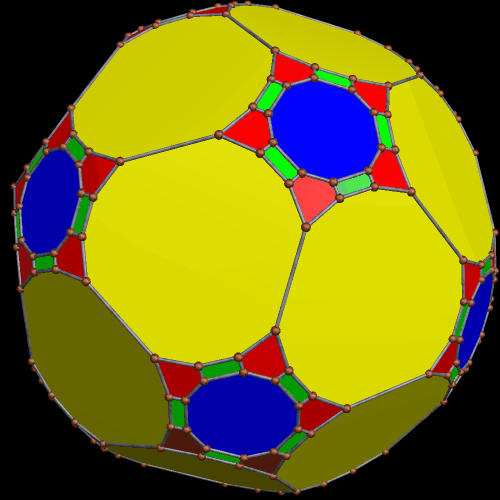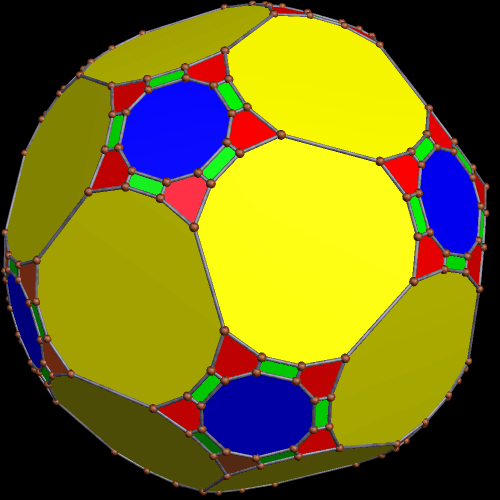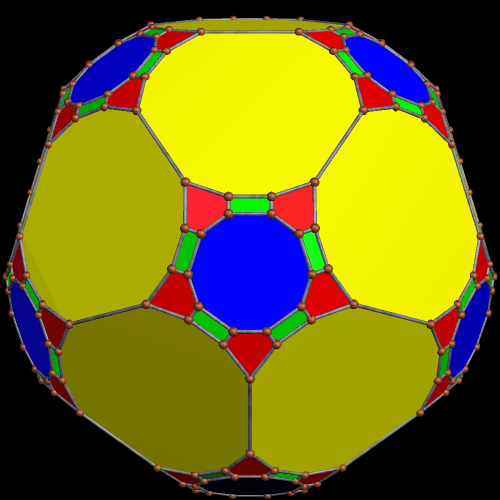
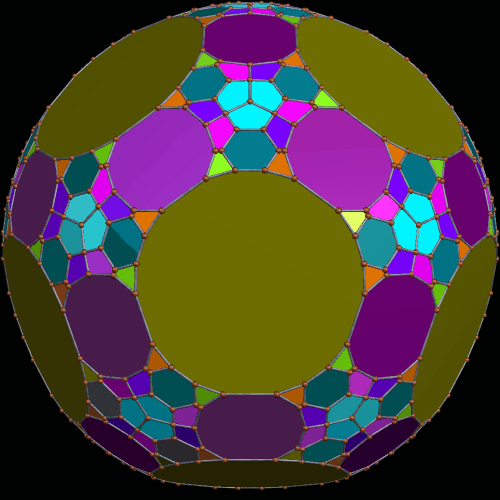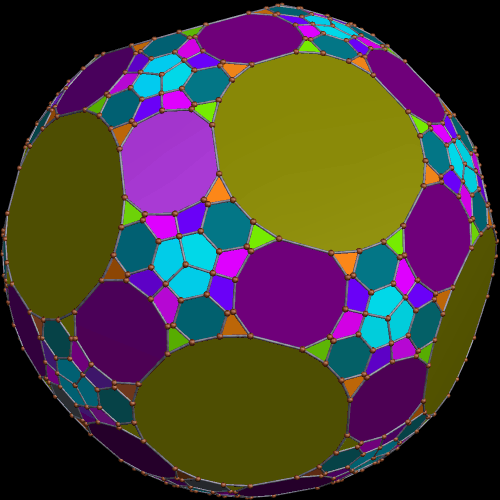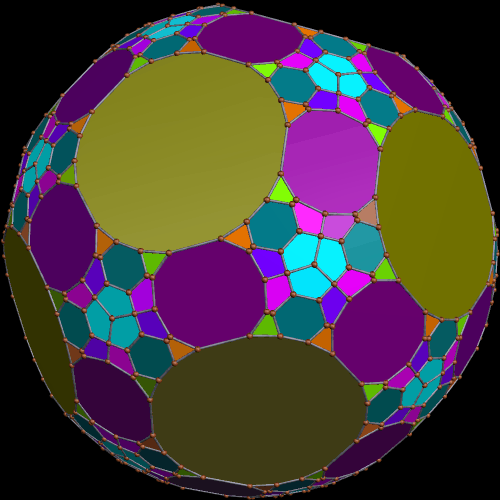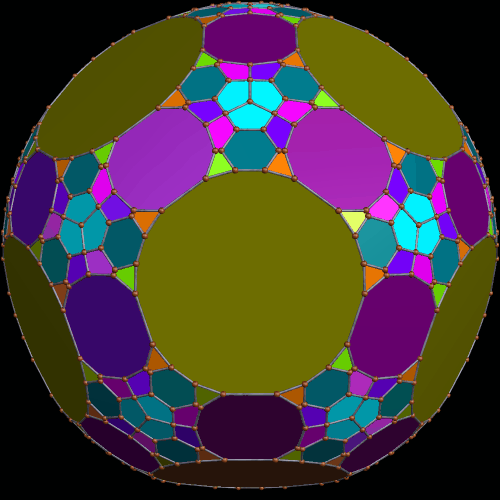
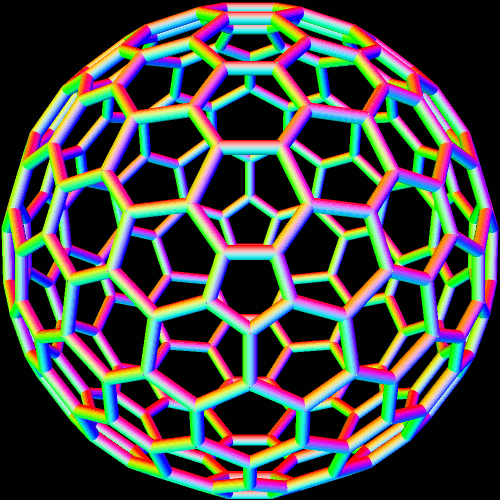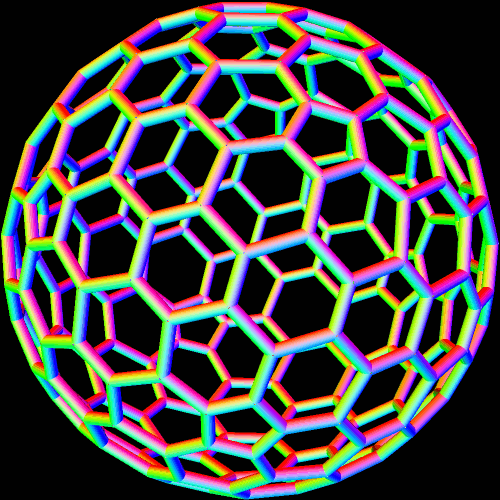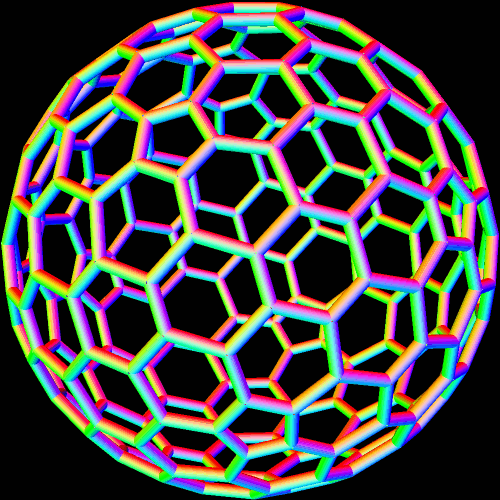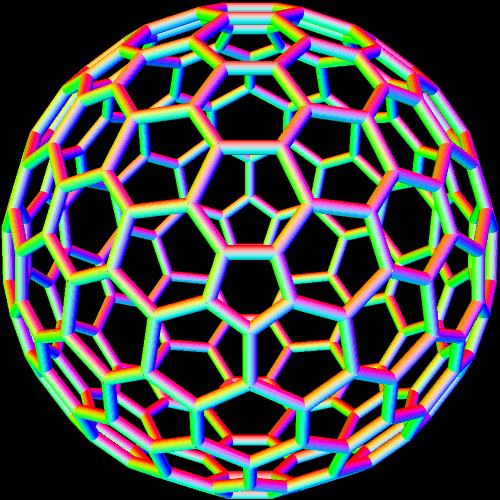
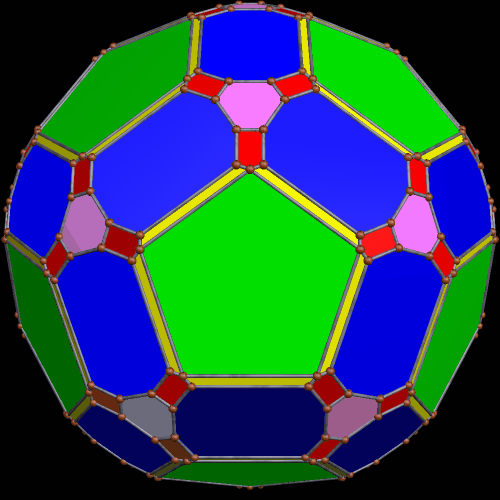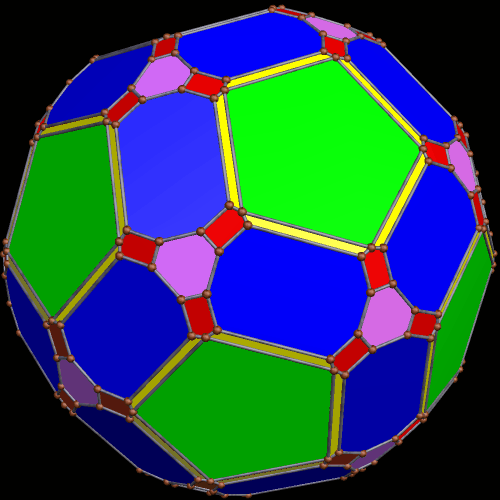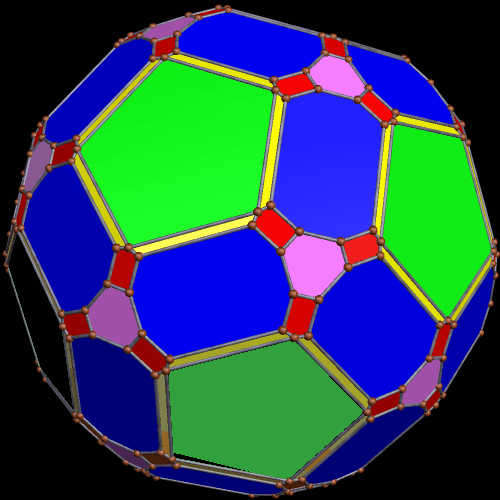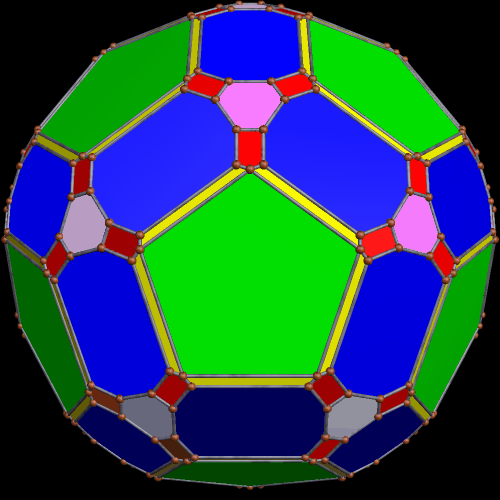
These two compounds, above and below, are duals. Also, in each of them, one polyhedron with icosidodecahedral symmetry is combined with a second polyhedron with cuboctahedral symmetry to form a compound with pyritohedral symmetry: the symmetry of a standard volleyball.
A program called Stella 4d was used to make these compounds, and create these images. It may be purchased, or tried for free, at this website.
I made these using Stella 4d, available here.
Pyritohedral symmetry, seen by example both above and below, is most often described at the symmetry of a volleyball:
[Image of volleyball found here.]
To make the rotating polyhedral compound at the top, from an octahedron and an icosahedron, I simply combined these two polyhedra, using Stella 4d, which may be purchased (or tried for free) here.
In the process, I demonstrated that it is possible to combine a figure with octahedral (sometimes called cuboctahedral) symmetry, with a figure with icosahedral (sometimes called icosidodecahedral) symmetry, to produce a figure with pyritohedral symmetry.
Now I can continue with the rest of my day. No matter what happens, I’ll at least know I accomplished something.
Note: icosidodecahedral symmetry, a term coined (as far as I know) by George Hart, means exactly the same thing as icosahedral symmetry. I simply use the term I like better. Also, a few of these, but not many, are chiral.
The images directly above and below show the shape of the most symmetrical 240-carbon-atom fullerene.
The image above is of the compound of five tetrahedra. This compound is chiral, and the next image is the compound of the compound above, and its mirror-image.
In the next two, I was experimenting with placing really big spheres at the vertices of polyhedra. The first one is the great dodecahedron, rendered in this unusual style, with the faces rendered invisible.
I made these using Stella 4d: Polyhedron Navigator. You may try this program for free at http://www.software3d.com/Stella.php.
RobertLovesPi.net 