I made this polyhedron (using Stella 4d, which you can try for free here) by modifying the tetrated dodecahedron. Its 32 faces include four regular hexagons, twelve squares, four equilateral triangles, and twelve isosceles trapezoids.
Tag Archives: symmetrohedra
Two Symmetrohedra Which Each Feature Four Regular Enneagons
This symmetrohedron has the following faces: four regular enneagons, four equilateral triangles, and twelve isosceles triangles with vertex angles of 43.5686 degrees. Its net is shown below.
If this polyhedron is stellated once, the result is another symmetrohedron — one with four enneagonal faces, as well as twelve kites. The angles in the kites are 116.762, 99.8348, 43.5686, and 99.8348 degrees, and their side lengths are in a 1:2.2946 ratio.
Finally, here is a net for this kite-and-enneagon solid.
I used Stella 4d: Polyhedron Navigator to make everything you see here. If you’d like to try this software for yourself, a free trial download is available at http://www.software3d.com/Stella.php.
A Polyhedral Journey, Starting With the Truncated Tetrahedron
Here’s the truncated tetrahedron. It is the simplest of the Archimedean solids.
I decided to “take a walk” with this polyhedron. First, I used Stella 4d (available here) to make the compound of this solid and its dual, the Catalan solid named the triakis tetrahedron.
Next, also using Stella (as I’m doing throughout this polyhedral journey), I formed the convex hull of this polyhedron — a solid made of kites and rhombi.
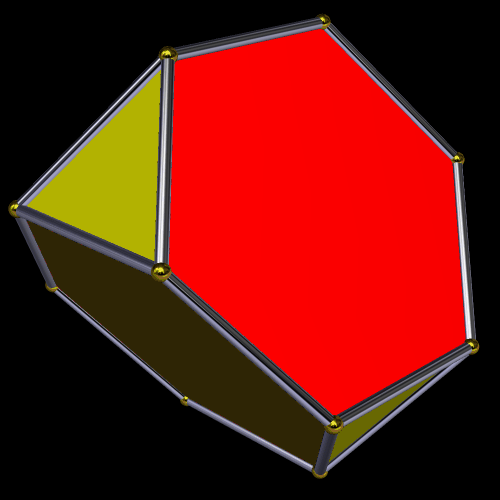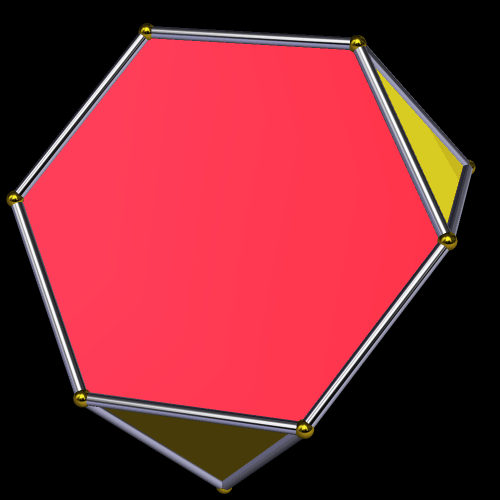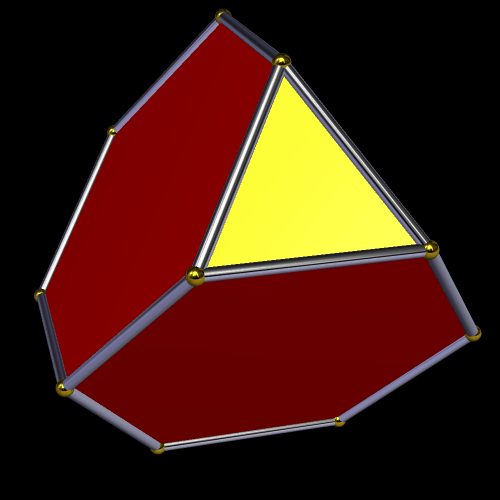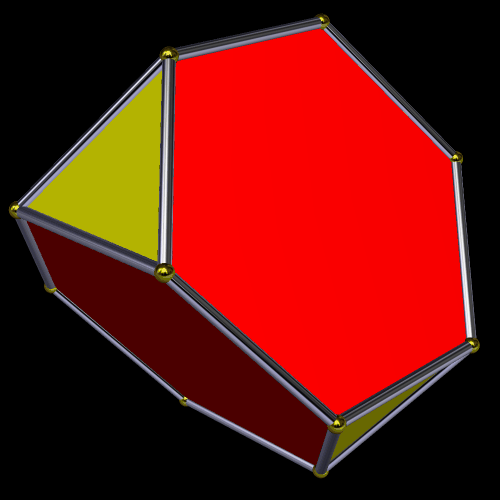
For the next polyehdron on this journey, I formed the dual of this convex hull. This solid is a symmetrohedron, featuring four regular hexagons, four equillateral triangles, and twelve isosceles triangles.
Next, I used a function of this program called “try to make faces regular.” Some this function works, and sometimes it doesn’t, if it isn’t mathematically possible — as it the case here, where the only thing that remained regular was the equilateral triangles. The hexagons in the resulting solid are equilateral, but not equiangular.
The next thing I did was to examine the dual of this latest polyhedron — another solid made of kites and rhombi, but with broader rhombi and narrower kites.
I then started stellating this solid. The 16th stellation was interesting, so I made a virtual model of it.
Stellating this twice more formed the 18th stellation, which turned out to be a compound of the cube and a “squished” version of the rhombic dodecahedron. This is when I decided that this particular polyhedral journey had come to an end.
A Symmetrohedron With All the Faces of the Icosidodecahedron, Plus Two Sets of Sixty Isosceles Triangles
This polyhedron is the dual of the rhombic octagonoid. I made it using Stella 4d, which you can try for free right here.
A Symmetrohedron Featuring Three Regular Pentagons, One Regular Hexagon, One Equilateral Triangle, and Three Each of Two Different Isosceles Trapezoids
I’m 90% sure this hasn’t been found before. It has three-fold pyramidal symmetry.
Here is its net.
I used Stella 4d to make this. You can try this program for free at this website.
A Symmetrohedron Featuring Twelve Regular Pentadecagons and Sixty Kites
I made this using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.
A Symmetrohedron Derived From the Rhombic Triacontahedron
I made this from a rhombic triacontahedron, using zonohedrification and faceting, with a program called Stella 4d. If you’d like to try this program for yourself, for free, you can do that at this website. This symmetrohedron’s faces include twenty equilateral triangles, thirty regular hexagons, and sixty kites.
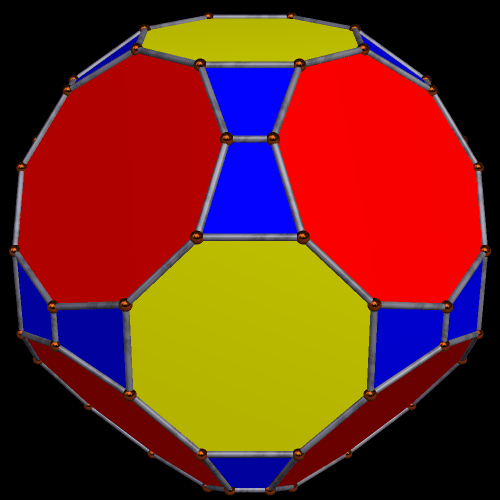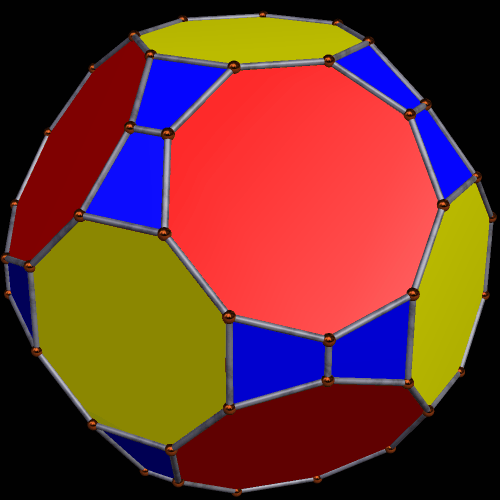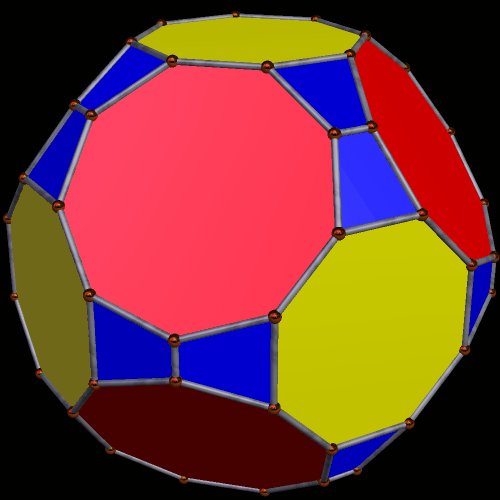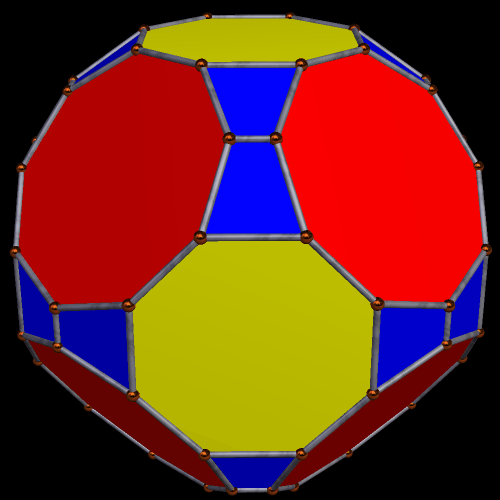
Two Symmetrohedra, Both of Which Feature Eight Regular Enneagons
The first of these, shown above, also includes six squares, 24 isosceles trapezoids, and twelve rectangles among its faces.
The second one, shown below, also includes among its faces six regular octagons, and twelve pairs of “bowtie” trapezoids.
I made both of these models using Stella 4d, which you can try for free here. The starting point for making them was the enneagonal-faced polyhedron found in this program’s built-in set of near-misses to the Johnson solids.
A Symmetrohedron With 62 Faces

In this solid, the quadrilaterals are all squares, and the red triangles are regular. The only irregular polygons are the dark blue triangles, which are obtuse and isosceles. I made this using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.
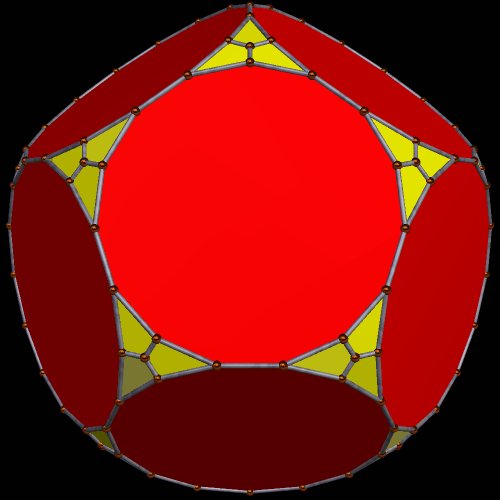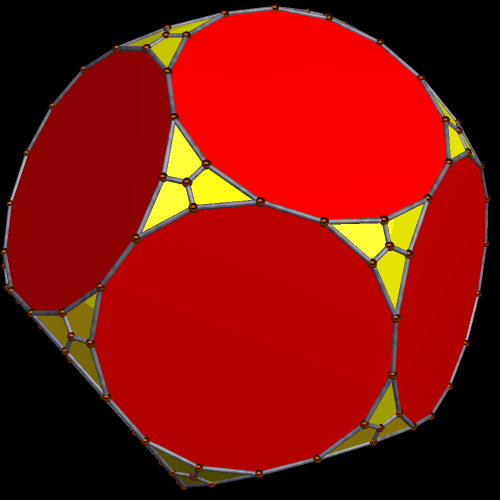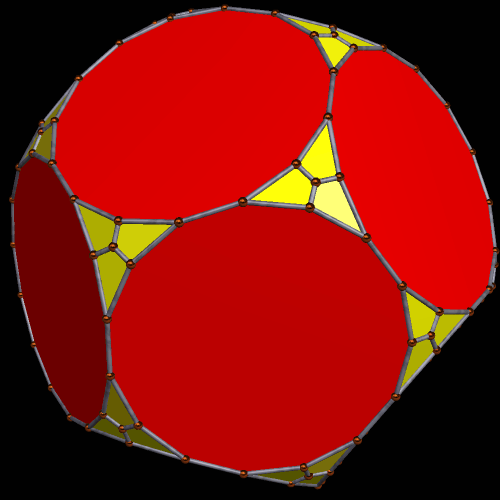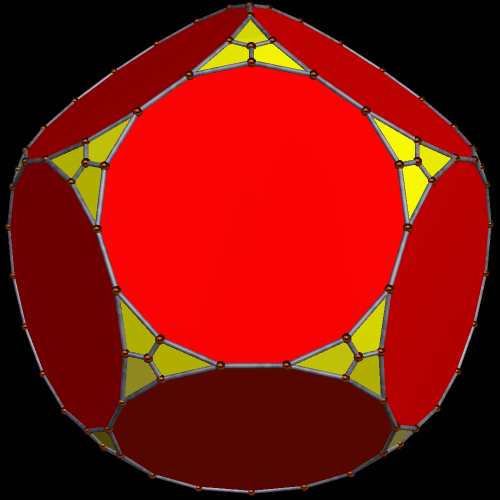
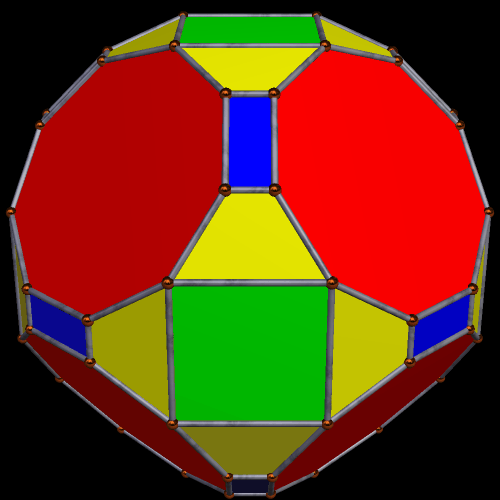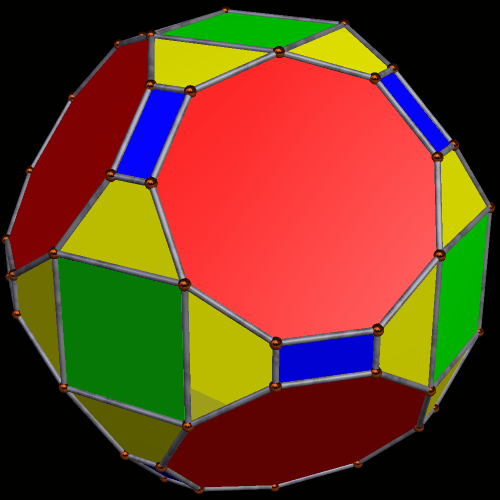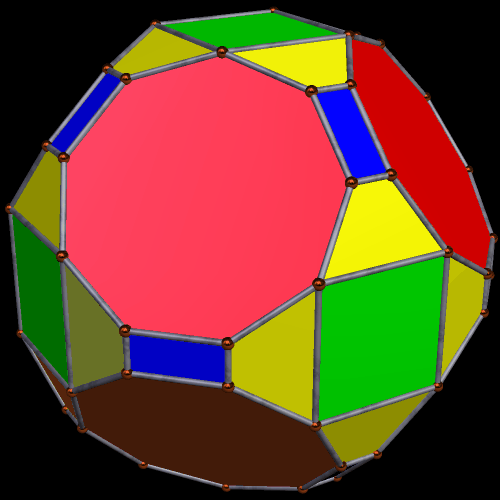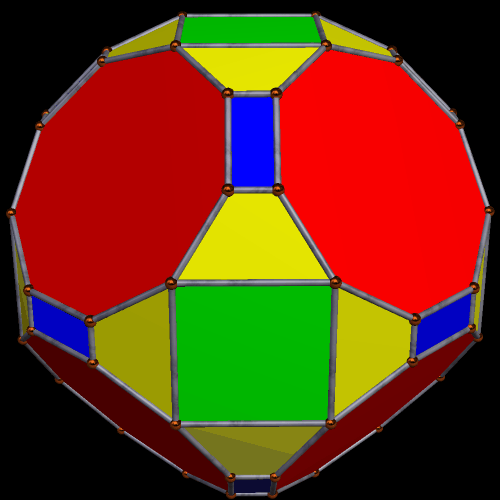
A Pair of Symmetrohedra Derived From the Rhombicosidodecahedron
To make this first symmetrohedron, I started with the rhombicosidodecahedron, augmented its thirty square faces with antiprisms, and then formed the convex hull of that solid. (I did all of this using Stella 34d: Polyhedron Navigator, which you can try for free right here.) The resulting polyhedron contains, as faces, twelve regular pentagons, twenty equilateral triangles, thirty squares, and sixty isosceles trapezoids, or 122 faces in all.
Next, I applied Stella’s “try to make faces regular” function, which produced the solid seen below. This had the effect of transforming the squares into rhombi, and changing the trapezoids so that, while still isosceles trapezoids, they closely resemble squares.