To enlarge any individual image, simply click on it.
These polyhedral images were created using Stella 4d: Polyhedron Navigator, a program you can find at http://www.software3d.com/Stella.php, with a free trial download available.
To enlarge any individual image, simply click on it.
These polyhedral images were created using Stella 4d: Polyhedron Navigator, a program you can find at http://www.software3d.com/Stella.php, with a free trial download available.
Each of these polyhedral images (any of which may be enlarged with a click) was created using Stella 4d: Polyhedron Navigator, and this program may be tried for free at http://www.software3d.com/Stella.php.
Also, a question, for regular readers of my blog — you have probably noticed that this post has a different format, but it’s just an experimental thing I’m trying out.
Do you prefer this style of polyhedra-post, or the format I usually use?

The polyhedron above is a tetrahedrally-symmetric polyhedron featuring regular dodecagons and triangles, as well as two types of trapezoidal faces.
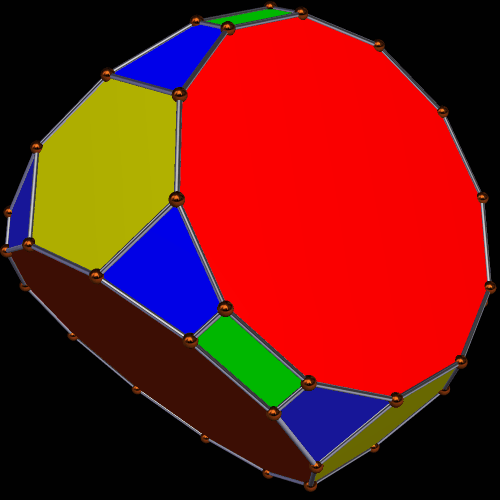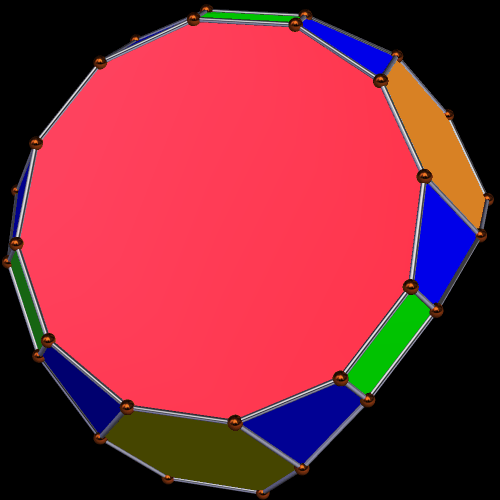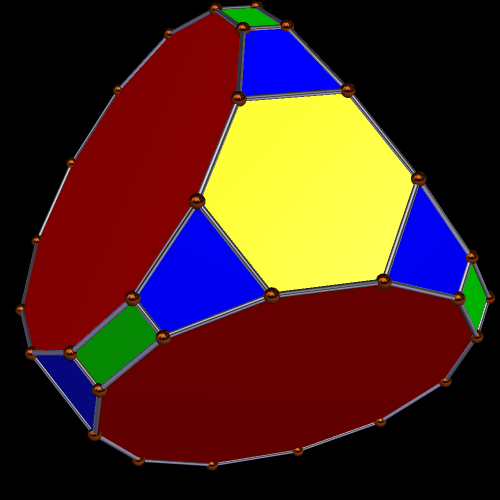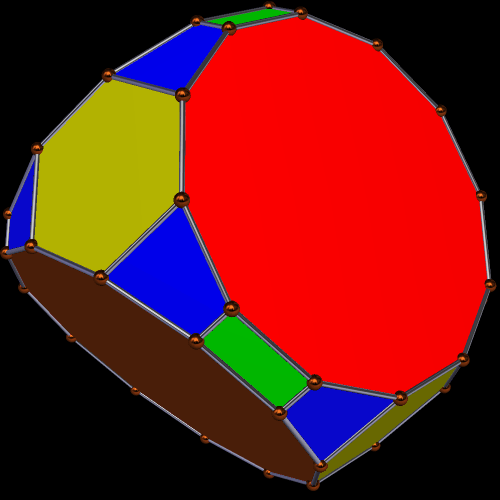
To make this second polyhedron from the first one, I first augmented each dodecagonal face with an antiprism, took the convex hull of the result, and then used the “try to make faces regular” function of the polyhedron-manipulation software I use, Stella 4d, which can be tried for free right here. The result is a polyhedron which maintains tetrahedral symmetry, and has, as faces, regular dodecagons and hexagons, as well as trapezoids and rectangles.
One of my early introductions to polyhedra came through playing the game Advanced Dungeons and Dragons (AD&D), which uses a standard seven-die set which includes the five Platonic Solids, plus two “d10s” (either ten-faced dipyramids or trapezohedra) which are used as a pair to generate random numbers from 1 to 100.

Assuming they are made with uniform density, these polyhedral dice are all “fair dice” — meaning that, for example, the d12 at the top of the picture has an equal chance of rolling any of 12 results, every time it is rolled.
I had also encountered, even earlier, a polyhedron which I believed (correctly) would not work as a fair die, since there is no reason to assume that rolling a cuboctahedron would result in equal probabilities for each face, given that some of the faces are squares, while others are triangles. This shape was familiar to me long before I heard (or even read) the word “cuboctahedron,” though, because I learned about it while watching “By Any Other Name,” an episode of the original Star Trek television series. At no point in this episode is the word “cuboctahedron” used, even though the entire crew of the USS Enterprise (with four exceptions) spend most of the episode in cuboctahedral form, as Lt. Uhura appears, at her bridge station, in this screenshot:

When examining uniform-density polyhedra to look for “fair dice,” therefore, one of the first things I look for is isohedrality — all faces must have the same shape, unlike the case of the cuboctahedron, but like the cases of AD&D dice. The next thing I examine is symmetry, hoping to find that a particular polyhedron’s symmetry gives no probability-advantage to any face(s). With these two tests in mind, I decided to see how many different fair, dodecahedral d12s I could find, including polyhedra which could work, whether or not such shapes had actually been used as real dice, at any time, by anyone.
When looking for dodecahedral “fair dice,” anyone with a familiarity with AD&D, or polyhedra, is likely to identify, first, the one with this shape:

The word “dodecahedron” literally refers simply to any polyhedra with twelve faces, but, in practice, most references to dodecahedra concern this twelve-faced polyhedron — the one found immediately above, and at the top of the photograph of a standard set of AD&D dice. When it is necessary to distinguish it from other twelve-faced polyhedra, this can be called, instead, the “Platonic dodecahedron.” It is the only dodecahedron to be both regular and convex; it also possesses icosidodecahedral symmetry, also known as icosahedral symmetry.
Although the pentagons in the Platonic dodecahedron are regular, it is also possible to make a fair-die polyhedron with irregular pentagons. Such a shape appears, occasionally, in the mineral pyrite, or FeS2, explaining the origin of the term “pyritohedral symmetry,” which is the symmetry-type of this particular dodecahedron: the pyritohedral dodecahedron.

There are actually an infinite number of slightly-different pyritohedral dodecahedra, as one can easily picture, by imagining a change in the length of the longest edges in the image directly above. However, for purposes of this survey, all possible pyritohedral dodecahedra are viewed as a single answer — the second, after the Platonic dodecahedron — to the question, “Which twelve-faced polyhedra would work as ‘fair dice?'”
The third answer to this question is provided by a completely different polyhedron, rather than a “warping” of the Platonic dodecahedron. In this third dodecahedron, the faces are rhombi, explaining why it is called the rhombic dodecahedron. Johannes Kepler studied this polyhedron extensively. Not just any rhombus will work, as a face, to make this polyhedron; it must be a specific type — one with diagonal-lengths in a ratio of one, to the square root of two.

This particular “fair die” occurs in nature, as crystals of the mineral garnet. There are also twelve-sided dice of this type now being sold, although finding them isn’t the easiest thing to do; one such retail outlet (in case you’d like to buy some rhombic dodecahedral dice) is The Dice Lab, which sells such dice at this website.
The rhombic dodecahedron, unlike the other dodecahedra shown above or below, has cuboctahedral symmetry, also known as octahedral symmetry. It is also the dual of the cuboctahedron — the same polyhedron about which I first learned as a young child, watching Star Trek.
Just as the first solution to this twelve-faced “fair dice” quest (the Platonic dodecahedron) can be “stretched” to find a second solution (the pyritohedral dodecahedron), this third solution (the rhombic dodecahedron) can be altered slightly to give a fourth solution, which I call the strombic dodecahedron, although it has other names as well (one, for example, is the “deltoidal dodecahedron”). To make this shape, one keeps the overall pattern of the rhombic dodecahedron, but allows the rhombi to be stretched into non-equilateral kites, as shown here:

As far as I know, no one has actually made such dice — but that doesn’t matter, for the point is that such dice could be made, and would be fair, given uniform density. This is actually a family of possible solutions, as was the case with the pyritohedral dodecahedron, because different versions of the strombic dodecahedron can be created by varying the length-ratio of the long and short edges of the figure. Such variants would still have the same name and symmetry-type, however, and that symmetry-type is tetrahedral.
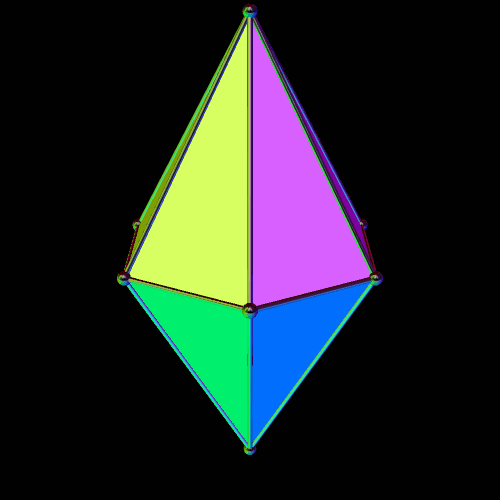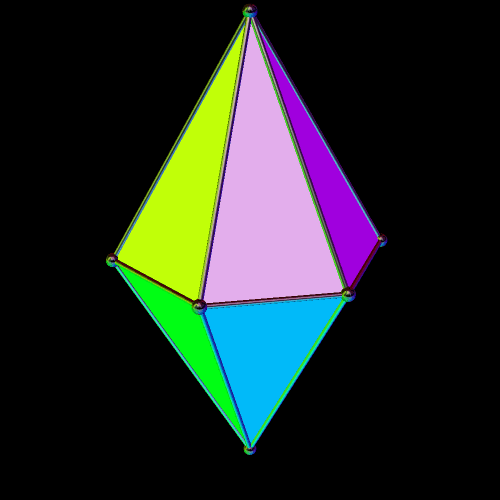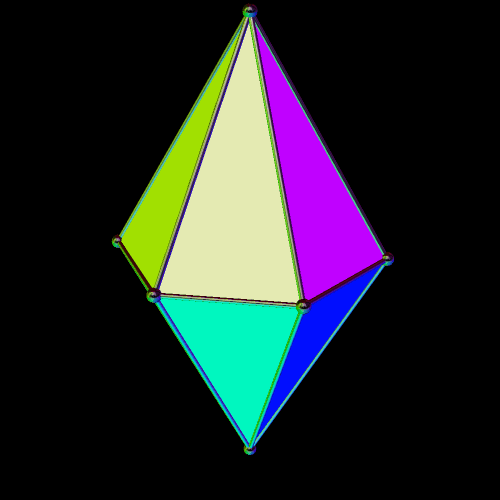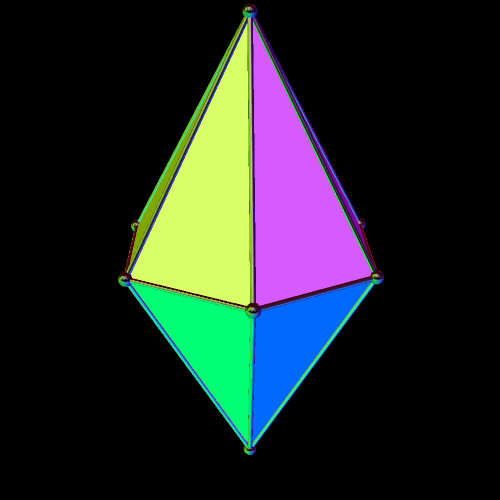
At least one other twelve-faced “fair die” can be made which also has tetrahedral symmetry: the Catalan solid known as the triakis tetrahedron, dual of the Archimedean truncated tetrahedron:

The triakis tetrahedron can be viewed as a Platonic tetrahedron, with each of its faces augmented by short, triangular pyramids which have lateral faces which are obtuse, isosceles triangles. The height of these short pyramids can be changed, while still leaving the overall polyhedron convex, over a range of heights; such altered versions, if not true duals of the Archimedean truncated tetrahedron, could simply be called non-Catalan tetrakis tetrahedra. The Catalan (and various convex non-Catalan) tetrakis tetrahedra are here collectively offered as the fifth type of twelve-faced polyhedra which can serve as fair dice.
The fourth and fifth solutions do have a problem, due to their tetrahedral symmetry: as a physical die, when rolled on a horizontal surface, the various strombic dodecahedra and triakis tetrahedra would land without a face pointing straight up, since they do not have parallel faces. This, however, merely means that, as fair dice, they wouldn’t be as convenient as the others; one might, for example, number their faces, and then pick up the die after it is rolled, to see which number ended up pointing straight down, rather than straight up. Other “workarounds” could also be devised. The need for such extra work, however, does not negate the fact that these polyhedra can be used as fair dice, for the problem was not set up with a convenience-requirement.
Further examination of a standard seven-piece AD&D dice set can lead to still more “fair d12s,” due to the presence of the d10s, also known, when used in pairs, as percentile dice. Most AD&D d10s have kites as faces (as seen in the metal dice set above), and are duals of pentagonal antiprisms, and so are themselves known as pentagonal trapezohedra (also known as “pentagonal deltohedra,” among other names). To get a similar fair die with twelve faces, rather than ten, one can simply start with a hexagonal antiprism, and then examine its dual: the hexagonal trapezohedron, which has six-fold dihedral symmetry:

By varying the long-to-short edge length ratio of the kite-faces in this polyhedron, the overall height of this polyhedron, as a function of its width, can be changed. This sixth solution is, therefore, another “infinite family” solution — as is the seventh solution, shown below, which can be easily made from the sixth solution (immediately above). To do so, mentally hold in place the bottom half of the hexagonal trapezohedra — but let the top half rotate for another 1/12 of a rotation before also “freezing” it. There is no need, now, for the zig-zagging “equator” in the polyhedron seen above — it can now be replaced with the coplanar edges of a hexagon, hidden inside the polyhedron, with the result that the twelve kites are replaced by a dozen isosceles triangles, turning the overall shape into a hexagonal dipyramid. These isosceles triangles must have vertex angles which measure less than 60° — in order to keep the figure from collapsing into something with no height, or with many edges which do not meet. Like the sixth solution before it, this seventh solution also has six-fold dihedral symmetry.
Next, here is a table which summarizes information about these seven possible dodecahedral “fair d12s.”
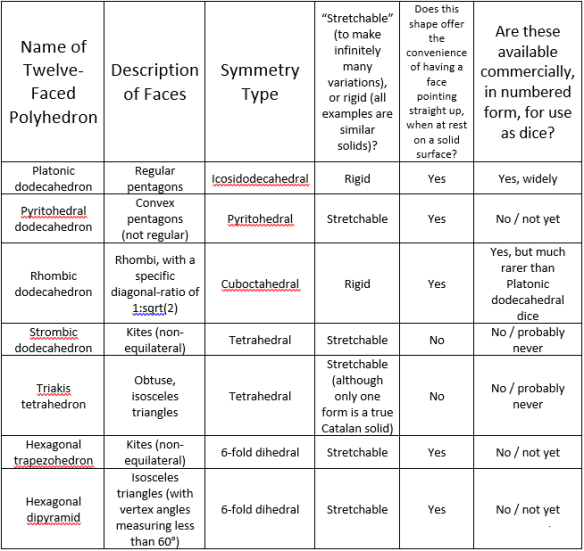
It is important to point out that this collection of seven solutions may not be complete, and I make no claim that it is. In fact, I strongly suspect it is not complete. It is simply the set of all solutions which have occurred to me — so far.
Some may wonder why I did not include the “barrel”-style d12s, which are also commercially available. This omission is no oversight. This particular style of d12 is not actually dodecahedral; it really has more than 12 faces, but is designed in such a way that it only has 12 faces which such dice can land on, and stay on — and that is not the same thing, at all. Also, I’m only looking for d12s here, which is why I did not include the “barrel”-style d4, even though it is a polyhedron which does have twelve faces.
Lastly, of the pictures in this post, the seven which feature rotating polyhedra were created using Stella 4d: Polyhedron Navigator, software which may be purchased, or tried for free, at this website.
All of these polyhedral images were created with Stella 4d, software you may try for free at http://www.software3d.com/Stella.php.












It’s quite an informal way to define it, but pyritohedral symmetry is the symmetry-type of a standard volleyball. These images of pyritohedral polyhedra were made using Stella 4d, software available at http://software3d.com/Stella.php.
While the polyhedron above, informally known as the “soccer ball,” has icosidodecahedral symmetry, its coloring-scheme does not. Instead, I colored the faces in such a way that the coloring-scheme has pyritohedral symmetry — the symmetry of a standard volleyball. This rotating image was made with Stella 4d, a program you can buy, or try for free, right here: http://www.software3d.com/Stella.php.
The President of the Zometool Corporation, Carlos Neumann, gave me a challenge, not long ago: find a solution to the Zome Cryptocube puzzle which uses only B0s, which I call “tiny blue struts.” For the Cryptocube puzzle, though, these “blue” struts actually appear white. Carlos knows me well, and knows I cannot resist a challenge involving Zome. Here is what I came up with, before the removal of the black cube, which is what the Zome Cryptocube puzzle starts with.
In a “pure” Crypocube solution, the red Zomeballs would also be white — not just the “blue” struts. However, when Carlos issued this challenge, I was at home, with all the white Zomeballs I own located at the school where I teach — so I used red Zomeballs, instead, since I had them at home, and did not wish to wait.
Here’s what this Cryptocube solution looks like, without the black cube’s black struts. You can still “see” the black cube, though, for the black Zomeballs which are the eight corners of the black cube are still present. As is happens, this particular Cryptocube solution has pyritohedral symmetry — better known as the symmetry of a standard volleyball.
While the Cryptocube puzzle is not currently available on the Zome website, http://www.zometool.com, it should be there soon — hopefully, in time for this excellent Zome kit to be bought as a Christmas present. Once a child is old enough so that small parts present no choking hazard, that child is old enough to start playing with Zome — and it is my firm belief that such play stimulates the intellectual growth of both children and adults. As far as a maximum age where Zome is an appropriate Christmas gift, the answer to that is simple: there isn’t one.
Also: while I do openly advertise Zome, I do not get paid to do so. I do this unpaid advertising for one reason: I firmly believe that Zome is a fantastic product, especially for those interested in mathematics, or for those who wish to develop an interest in mathematics — especially geometry. Also, Zome is fun!
I’ve been shown, by the program’s creator, a function of Stella 4d which was previously unknown to me, and I’ve been having fun playing around with it. It works like this: you start with a polyhedron with, say, icosidodecahedral symmetry, set the program to view it as a figure with only tetrahedral symmetry (that’s the part which is new to me), and then stellate the polyhedron repeatedly. (Note: you can try a free trial download of this program here.) Several recent posts here have featured polyhedra created using this method. For this one, I started with the snub dodecahedron, one of two Archimedean solids which is chiral.
Using typical stellation (as opposed to this new variety), stellating the snub dodecahedron once turns all of the yellow triangles in the figure above into kites, covering each of the red triangles in the process. With “tetrahedral stellation,” though, this can be done in stages, producing a greater variety of snub-dodecahedron variants which feature kites. As it turns out, the kites appear twelve at a time, in four sets of three, with positions corresponding to the vertices (or the faces) of a tetrahedron. Here’s the first one, featuring one dozen kites.
Having done this once (and also changing the colors, just for fun), I did it again, resulting in a snub-dodecahedron-variant featuring two dozen kites. At this level, the positions of the kite-triads correspond to those of the vertices of a cube.
You probably know what’s coming next: adding another dozen kites, for a total of 36, in twelve sets of three kites each. At this point, it is the remaining, non-stellated four-triangle panels, not the kite triads, which have positions corresponding to those of the vertices of a cube (or the faces of an octahedron, if you prefer).
Incoming next: another dozen kites, for a total of 48 kites, or 16 kite-triads. The four remaining non-stellated panels of four triangles each are now arranged tetrahedrally, just as the kite-triads were, when the first dozen kites were added.
With one more iteration of this process, no triangles remain, for all have been replaced by kites — sixty (five dozen) in all. This is also the first “normal” stellation of the snub dodecahedron, as mentioned near the beginning of this post.
From beginning to end, these polyhedra never lost their chirality, nor had it reversed.