Octagons, Hexagons, and Squares

Posted on 31 December 2014 by RobertLovesPi

A Survey of Polyhedra with Pyritohedral Symmetry

Posted on 24 December 2014 by RobertLovesPi

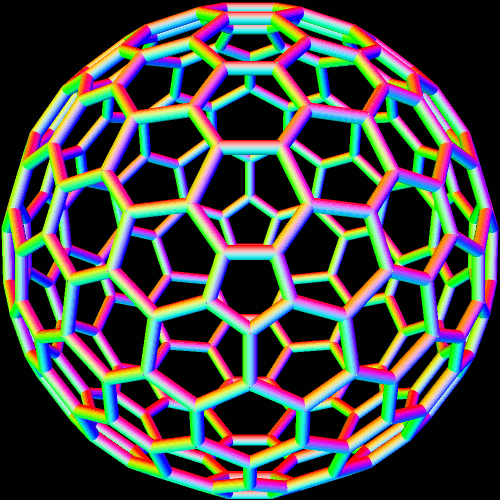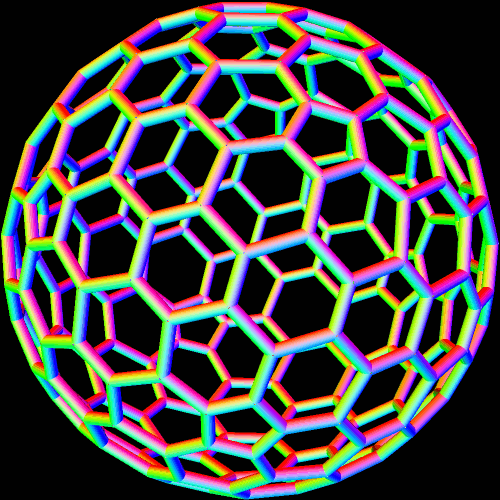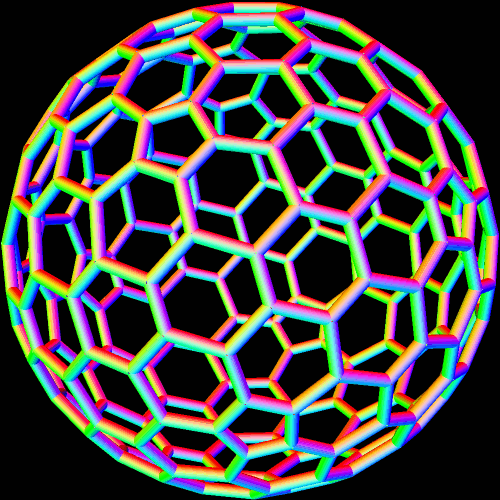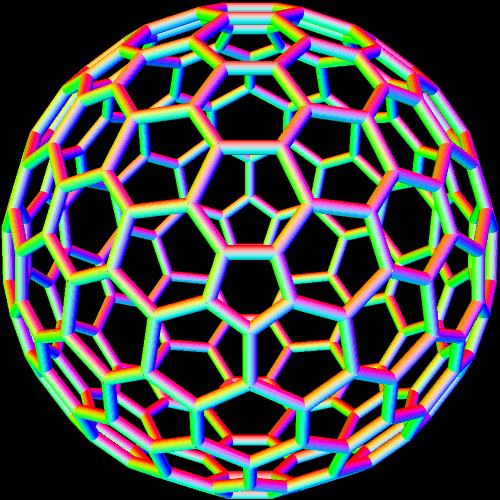
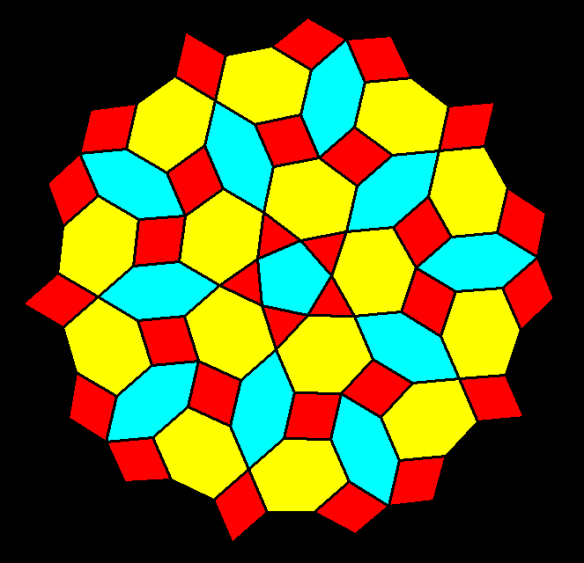
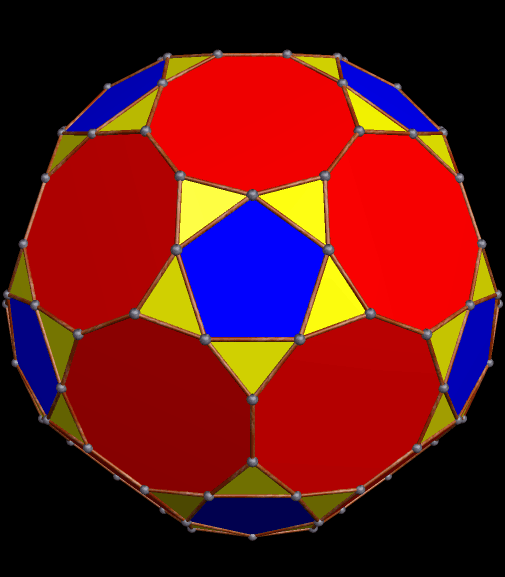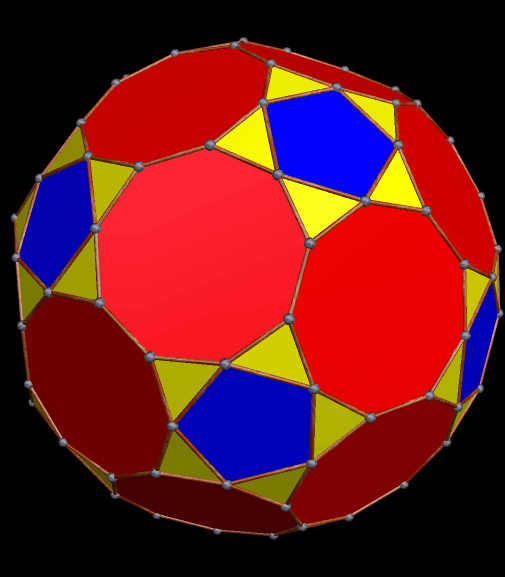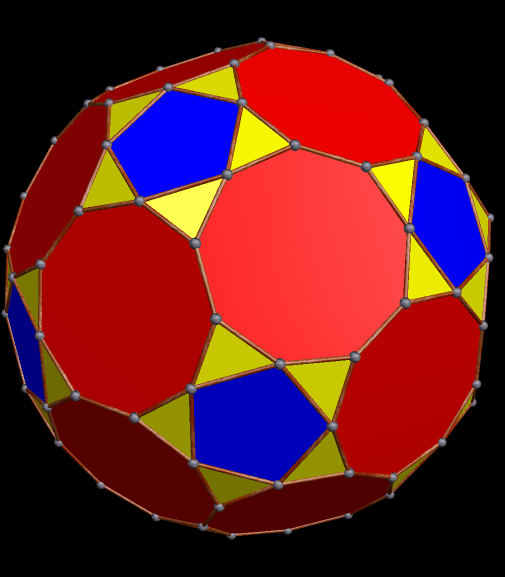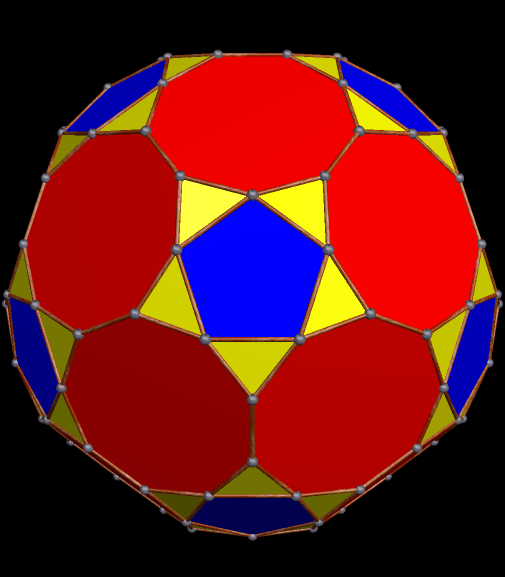
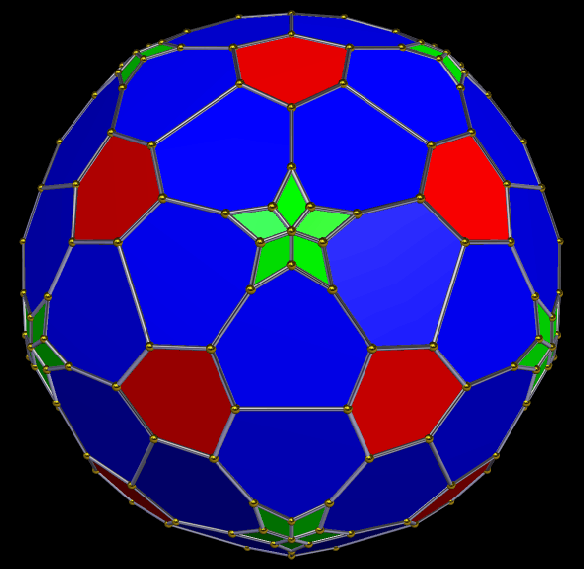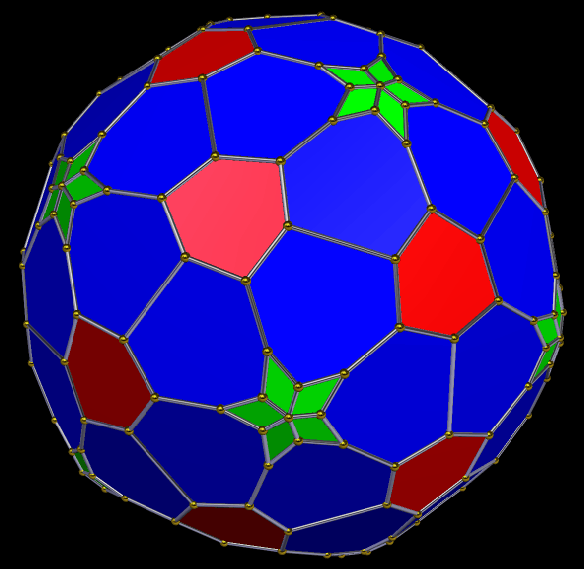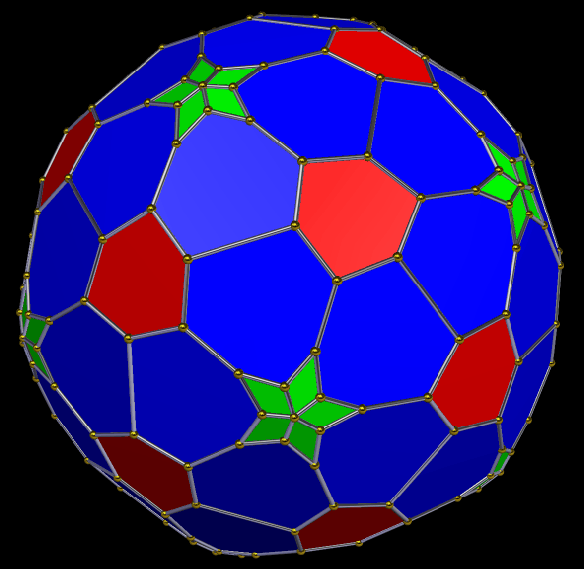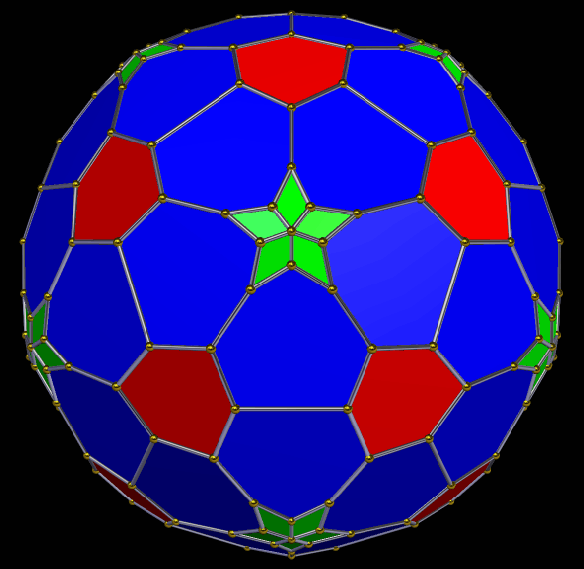
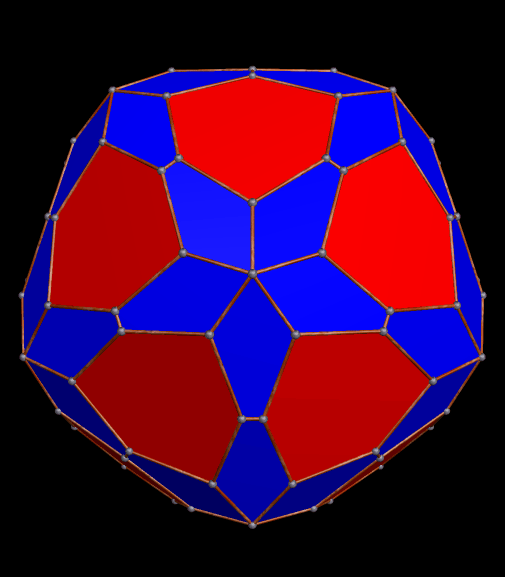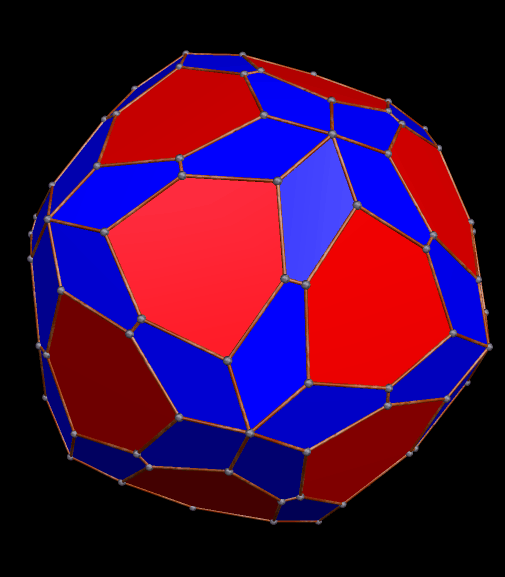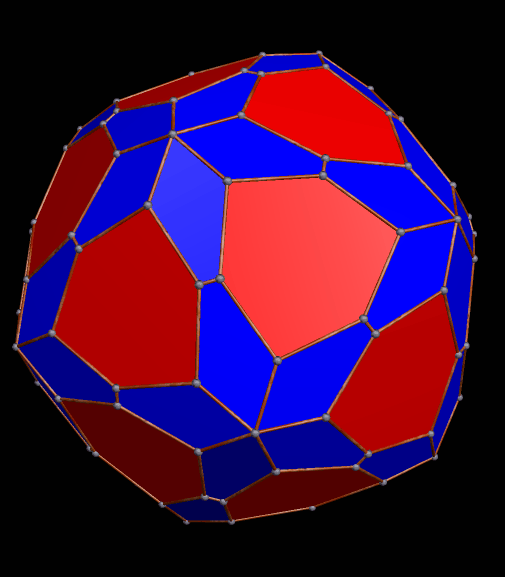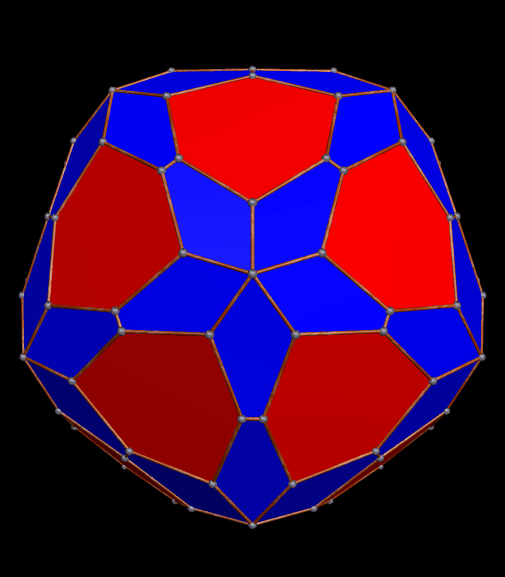
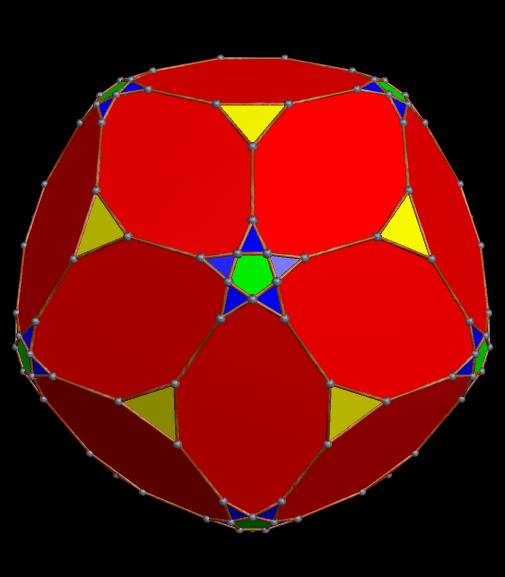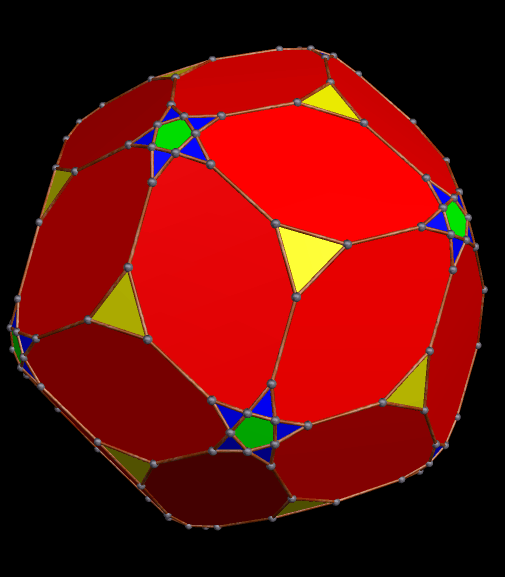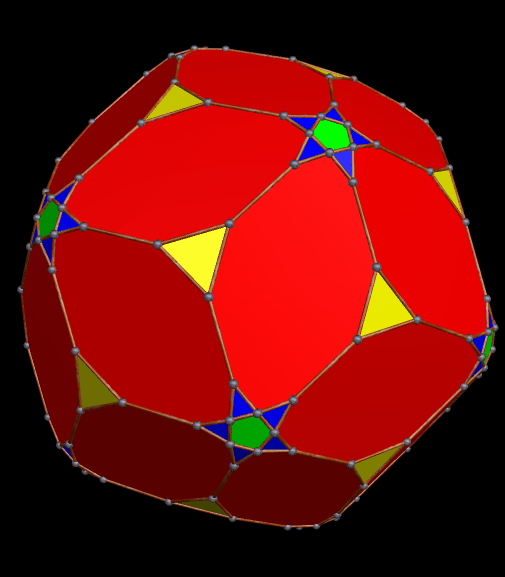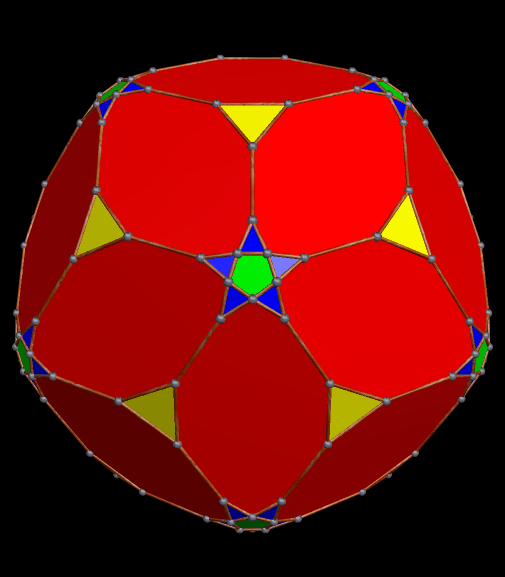
The simplest way for many to understand pyritohedral symmetry is simply to realize that it is the symmetry of the seams in a volleyball. The first time I encountered this unusual symmetry-type was in the golden icosahedron I blogged about here, a figure which much resembles this pyritohedral icosahedron, except the dozen isosceles triangles in this one have a leg-to-base ratio which is not the golden ratio.

Earlier today, I went on a search for polyhedra with pyritohedral symmetry. I found several, but the worthwhile findings from the search are far from exhausted. Here are some others I found, exploring and manipulating polyhedra using Stella 4d, which you can try at this website.

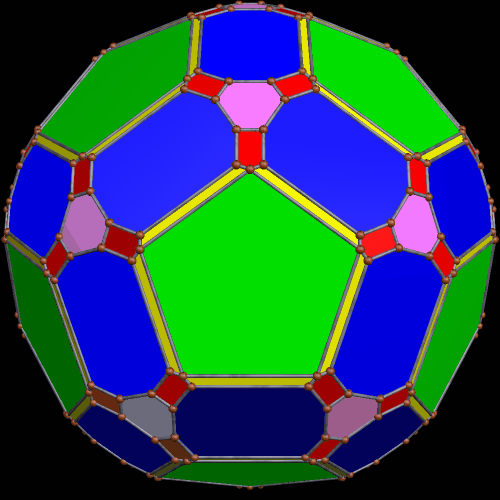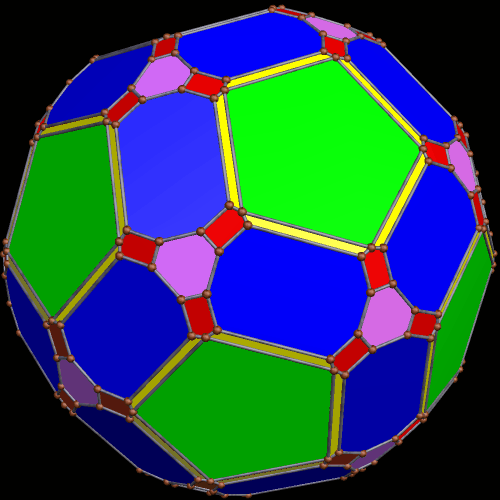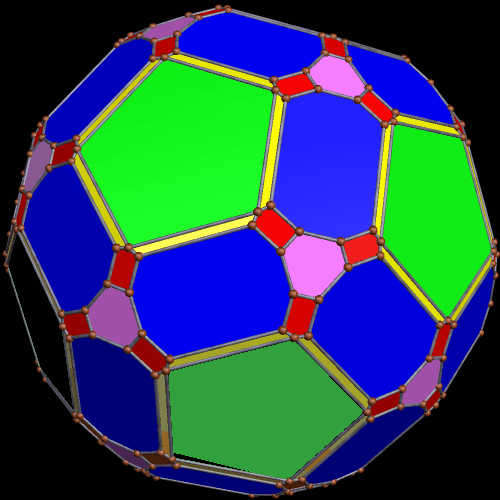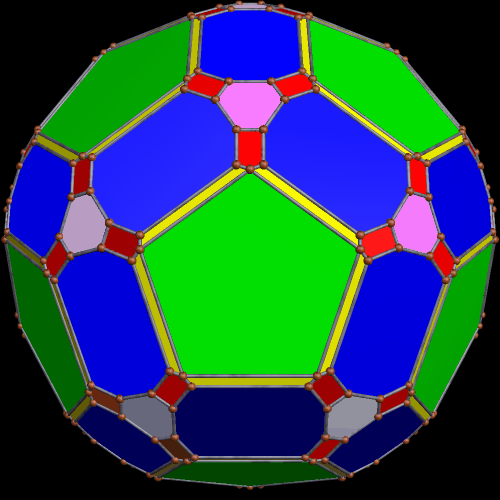
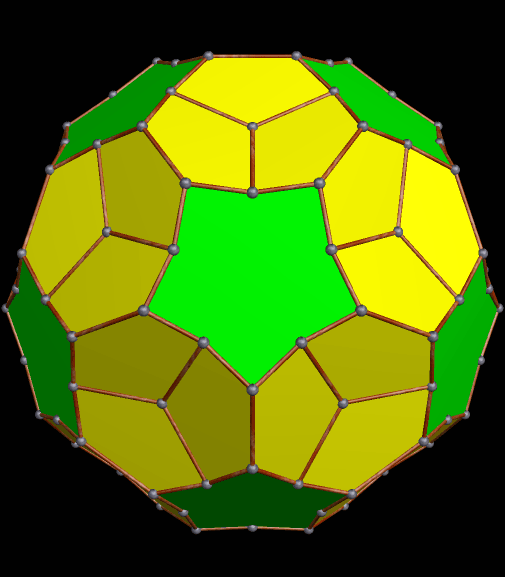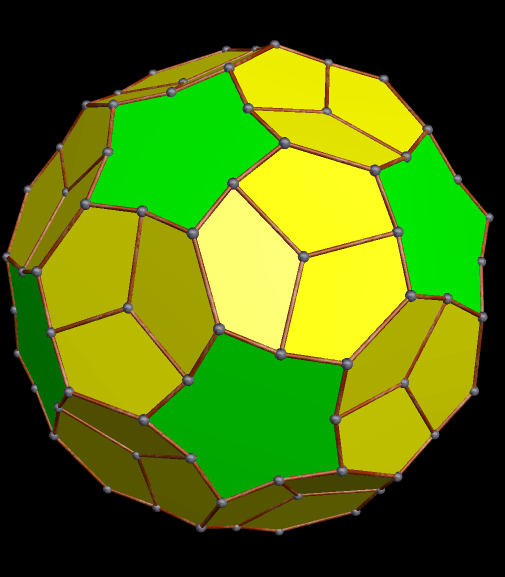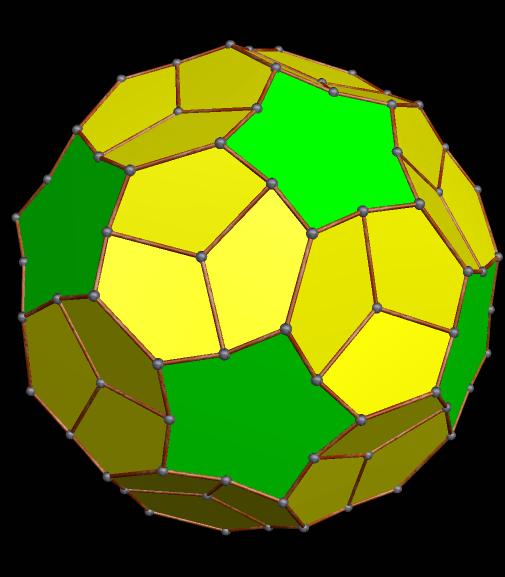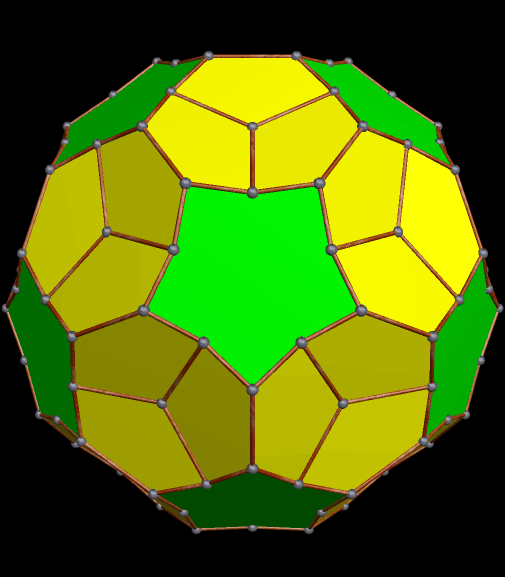
In the version of the pyritohedral icosahedron above, the twelve green triangles have become heptagons which use very short sides to approximate triangles. The one below is of a similar figure, but one in which truncations has happened, so I call it a truncated pyritohedral icosahedron.

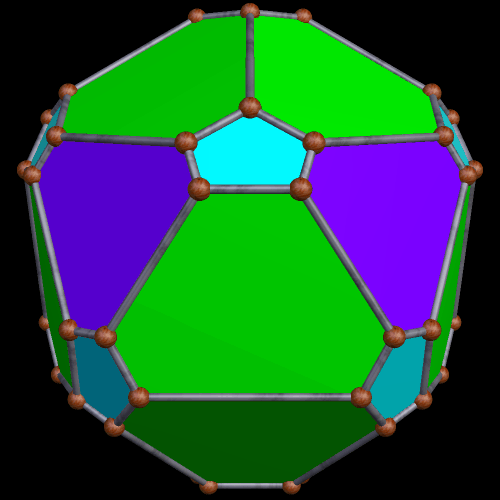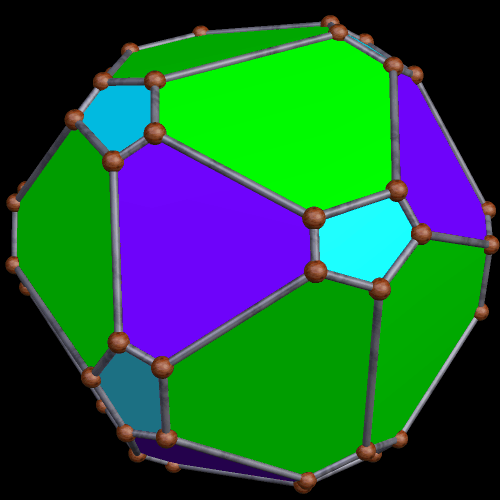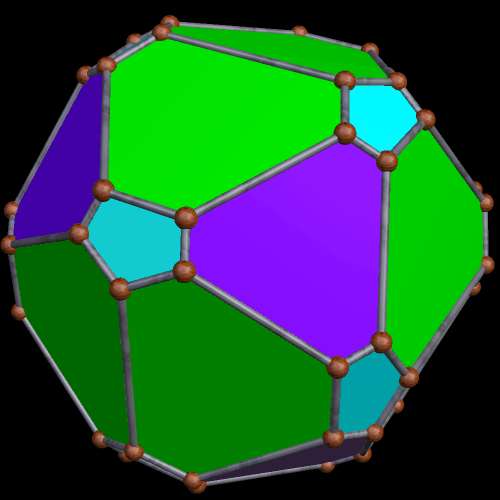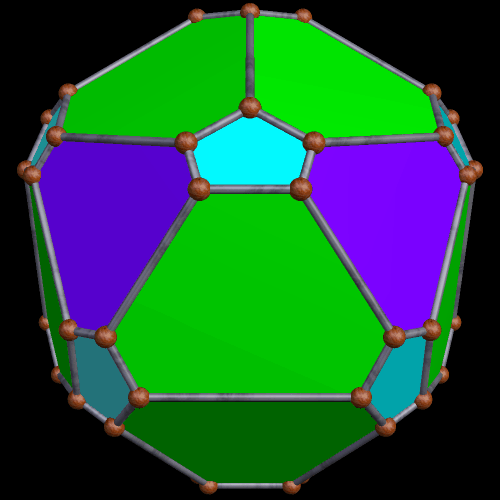
There also exist many pyritohedral polyhedra based, more or less, on the cube. These are a few I have found:

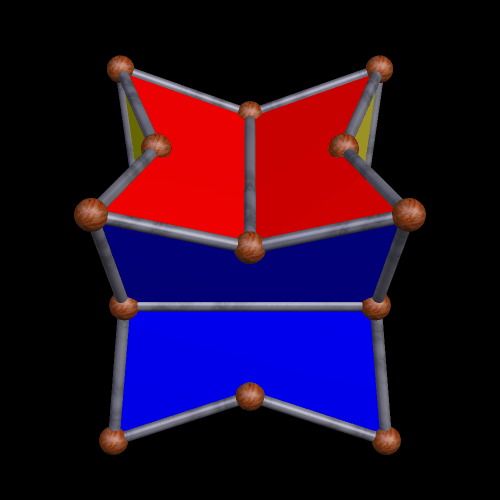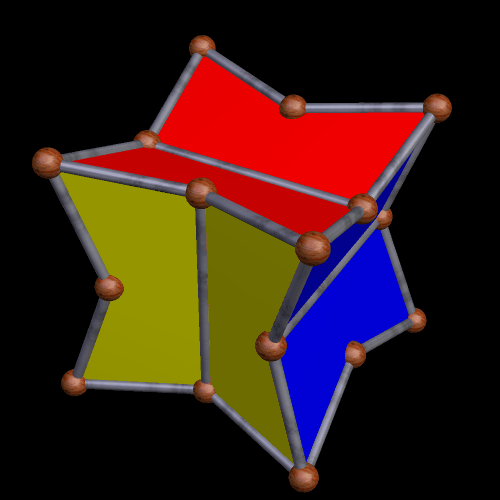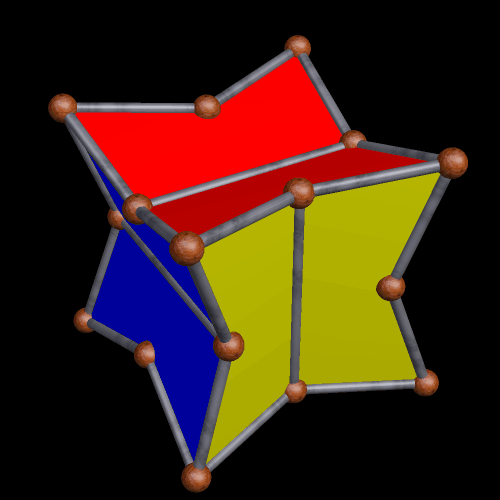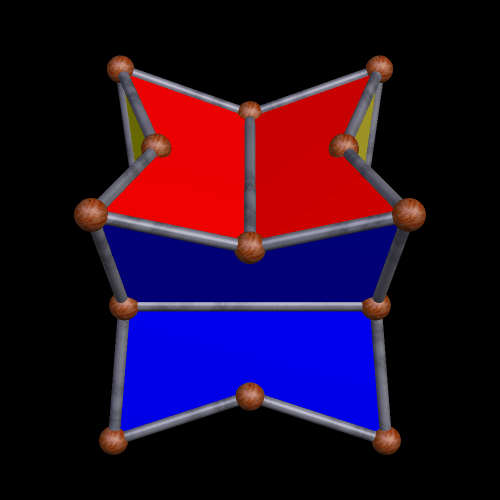
Now, is this next one a pyritohedral cube, or a pyritohedral dodecahedron? A case could be made for either, so it inhabits a “gray zone” between varying categories.

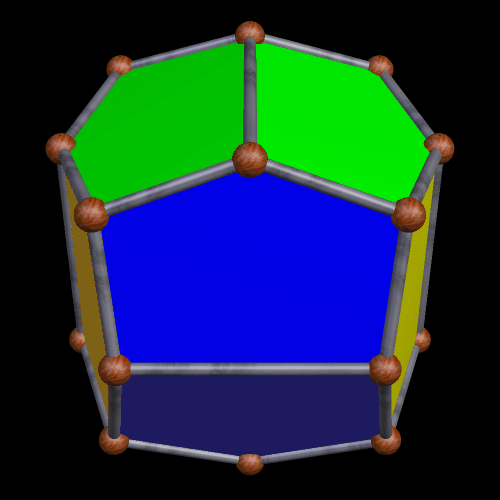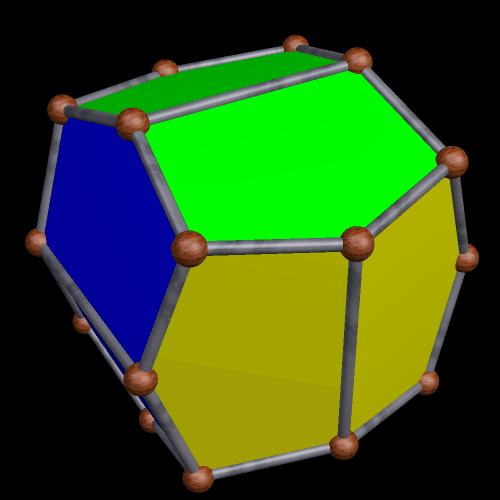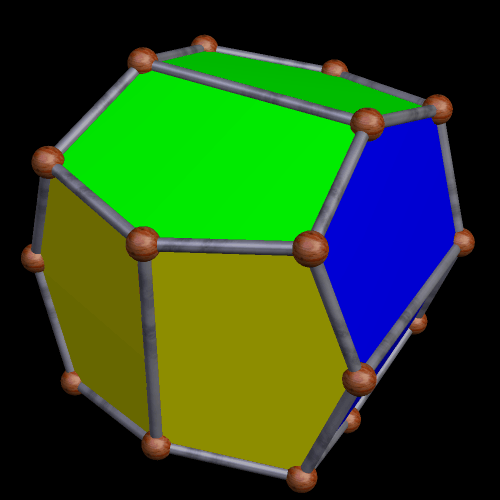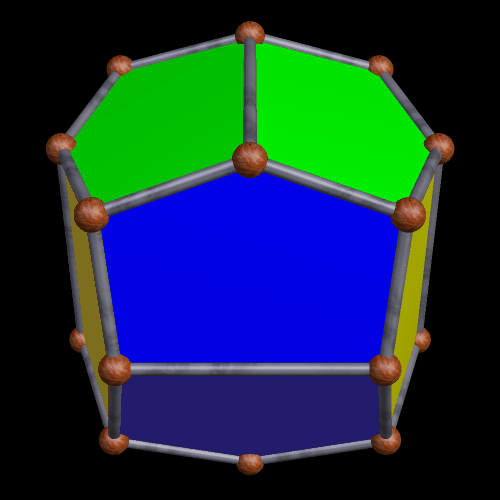
Here is a pyritohedral icosidodecahedron:

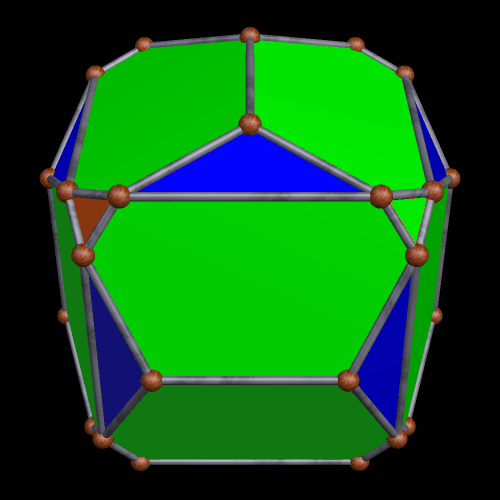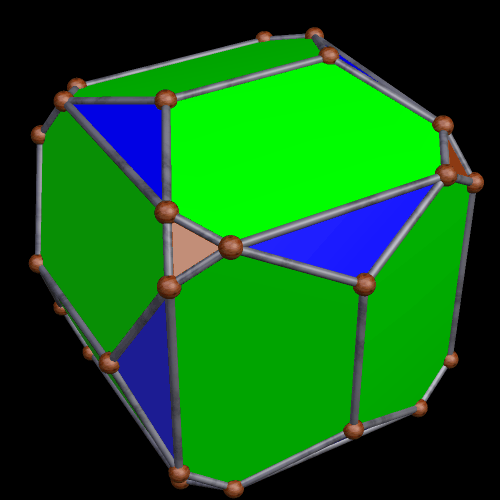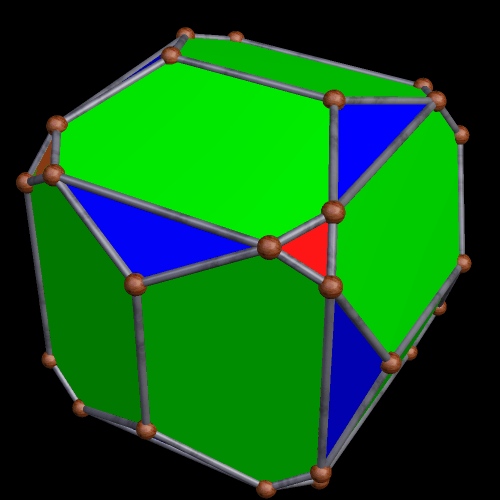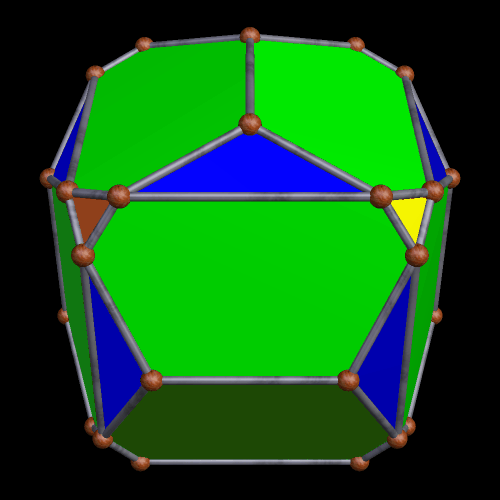
This one could probably be described in multiple ways, also, but it looks, to me, like a rhombic dodecahedron with its six four-valent vertices being double-truncated in a pyritohedral manner, with pairs of isosceles trapezoids appearing where the truncations took place.

One thing that this one, and the last, have in common is that the largest faces are heptagons. It appears to be a pyritohedral dodecahedron which has been only partially truncated.

This survey could not have been performed without a program called Stella 4d, which I rely on heavily for polyhedral investigations. It may be purchased, or tried for free, at http://www.software3d.com/Stella.php.

Thirty-Three Polyhedra with Icosidodecahedral Symmetry

Posted on 20 December 2014 by RobertLovesPi

Note: icosidodecahedral symmetry, a term coined (as far as I know) by George Hart, means exactly the same thing as icosahedral symmetry. I simply use the term I like better. Also, a few of these, but not many, are chiral.

The images directly above and below show the shape of the most symmetrical 240-carbon-atom fullerene.

The image above is of the compound of five tetrahedra. This compound is chiral, and the next image is the compound of the compound above, and its mirror-image.

In the next two, I was experimenting with placing really big spheres at the vertices of polyhedra. The first one is the great dodecahedron, rendered in this unusual style, with the faces rendered invisible.

I made these using Stella 4d: Polyhedron Navigator. You may try this program for free at http://www.software3d.com/Stella.php.

A Radial Tessellation of Regular Decagons and Bowtie Hexagons

Posted on 20 December 2014 by RobertLovesPi

This tiling-pattern could be continued indefinitely, while still maintaining its five-fold radial symmetry, giving it the overall appearance of a pentagon.

Four Non-Convex Polyhedra with Icosidodecahedral Symmetry

Posted on 15 December 2014 by RobertLovesPi

All of these were made with Stella 4d, a program you can find at http://www.software3d.com/Stella.php.

On Icosahedra, and Pyritohedral Symmetry

Posted on 23 November 2014 by RobertLovesPi

In this icosahedron, the four blue faces are positioned in such a way as to demonstrate tetrahedral symmetry. The same is true of the four red faces. The remaining twelve faces demonstrate pyritohedral symmetry, which is much less well-known. It was these twelve faces that I once distorted to form what I named the “golden icosahedron” (right here: https://robertlovespi.wordpress.com/2013/02/08/the-golden-icosahedron/), but, at that point, I had not yet learned the term for this unusual symmetry-type.

To most people, the most familiar object with pyritohedral symmetry is a volleyball. Here is a diagram of a volleyball’s seams, found on Wikipedia.

Besides the golden icosahedron I found, back in 2013, there is another, better-known, alteration of the icosahedron which has pyritohedral symmetry, and it is called Jessen’s icosahedron. Here’s what it looks like, in this image, which I found at http://en.wikipedia.org/wiki/Jessen%27s_icosahedron.

The rotating icosahedron at the top of this post was made using Stella 4d, a program which may be purchased, or tried for free (as a trial version) at http://www.software3d.com/Stella.php.

Two Views of a Mandala with Fivefold Symmetry

Posted on 11 September 2014 by RobertLovesPi

A Polyhedral Boomerang, in Flight

Posted on 17 August 2014 by RobertLovesPi

Most of the polyhedra I post here have one of the symmetry-types which are collectively called “polyhedral” symmetry: tetrahedral, cuboctahedral, icosidodecahedral, or chiral variants of these. For polyhedral representations of most real-world objects, though, such as this one, these symmetry-types must be abandoned.

Image credit: I made this using Stella 4d, available at www.software3d.com/Stella.php.

A Collection of Rotating Polyhedra with Cuboctahedral Symmetry

Posted on 17 August 2014 by RobertLovesPi

I have received a request to slow down the rotational speed of the polyhedral models I make and post here, and am going to try to do exactly that. First, though, I need to empty my collection of already-made image files which haven’t yet been posted, so that I can start again, with models which rotate more slowly, after deleting all the “speedy” ones. From my backlog of polyhedral images to post, then, here are some which have cuboctahedral symmetry.

This last one actually has the symmetry of a snub cube — a chiral variant of “normal” cuboctahedral symmetry.

All these images were created using Stella 4d: Polyhedron Navigator. If you’d like to try this program for yourself, the website to visit for a free trial download is www.software3d.com/Stella.php.

A Collection of Rotating Polyhedra with Icosidodecahedral Symmetry

Posted on 17 August 2014 by RobertLovesPi

I’ve received a request to slow down the rotational speed of the polyhedral models I make and post here, and am going to try to do exactly that. First, though, I need to empty my collection of already-made image files which haven’t yet been posted, so that I can start again, with models which rotate more slowly, after deleting all the “speedy” ones. From my backlog of polyhedral images to post, then, here are most of the ones with icosidodecahedral symmetry.

The next one shown has 362 faces — the closest I have come, so far, to a polyhedron with a number of faces which matches the number of days in a year.

The next one is a variant of the rhombic enneacontahedron, with that polyhedron’s wide rhombic faces replaced by kites, and its narrow rhombi replaced by pairs of isosceles triangles.

I call this next one a “thrice-truncated rhombic triacontahedron.”

In the remaining polyhedral images in this post, some faces have been rendered invisible. I do this, on occasion, either so that the front and back of the polyhedra can be seen at the same time, or simply for aesthetic reasons.

All of these images were created using Stella 4d: Polyhedron Navigator. If you’d like to try this program for yourself, the website to visit for a free trial download is www.software3d.com/Stella.php.