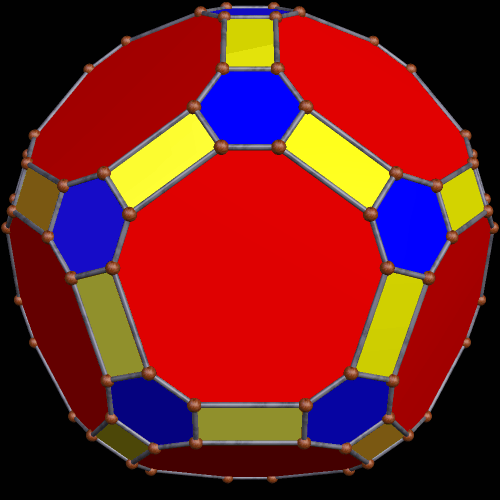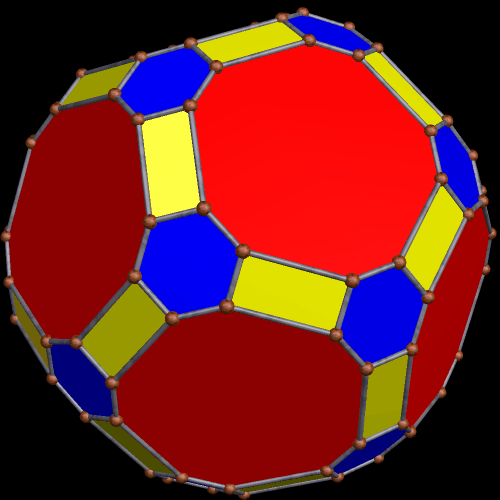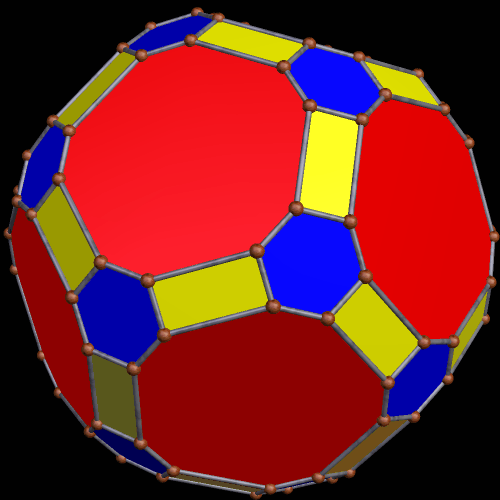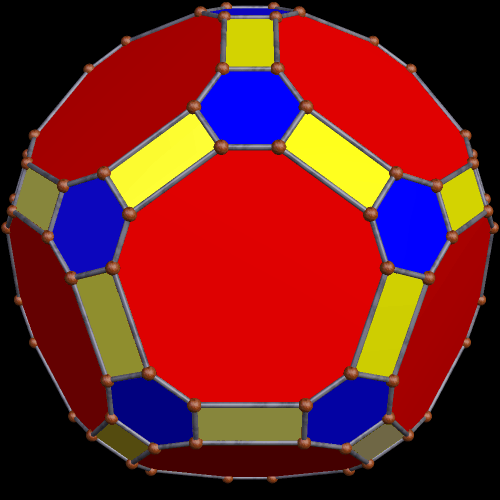
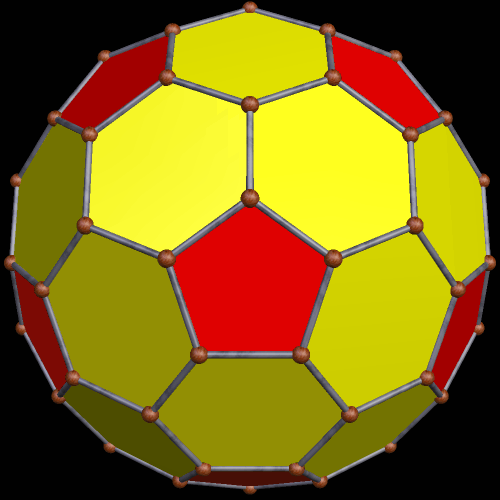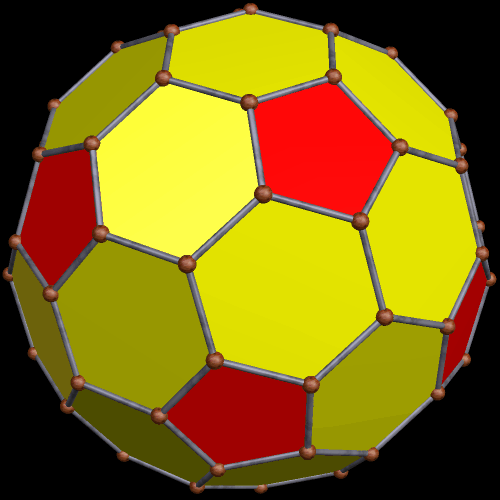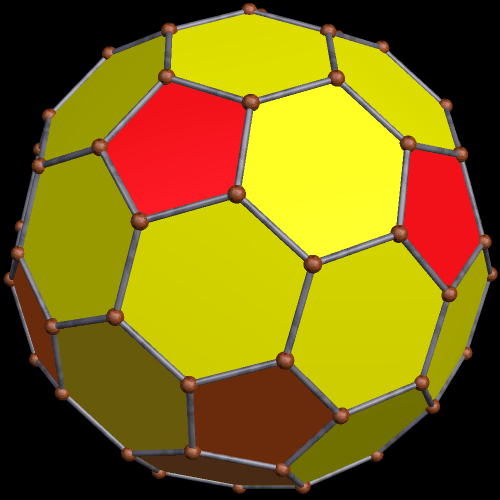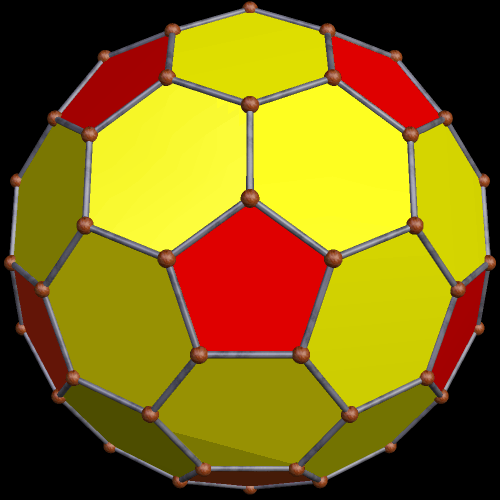
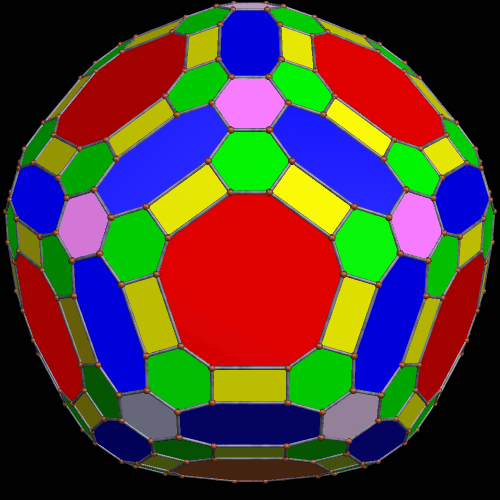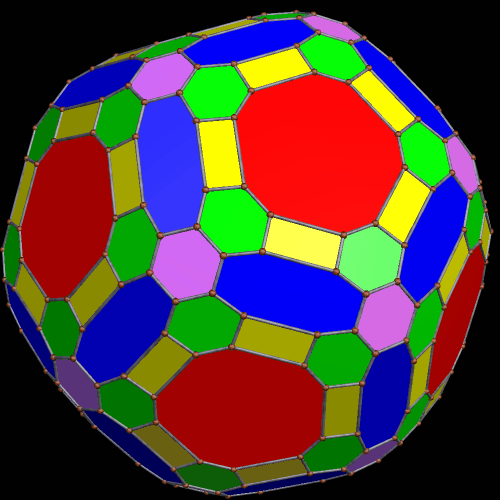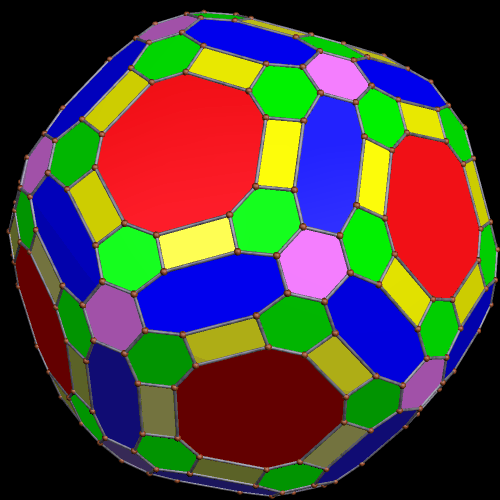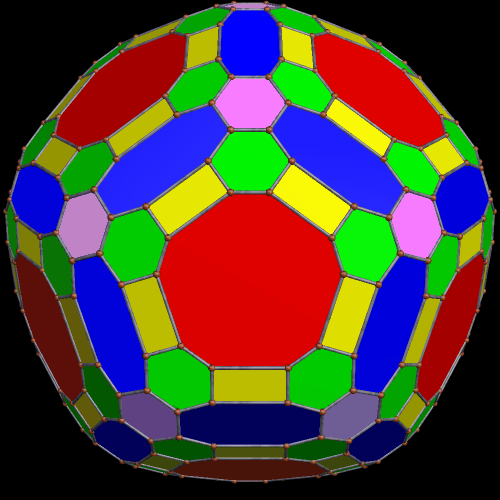
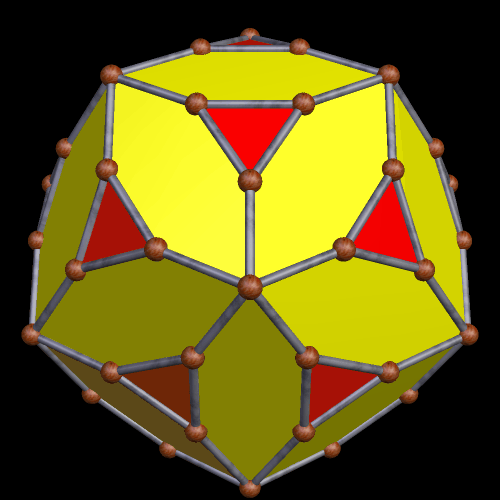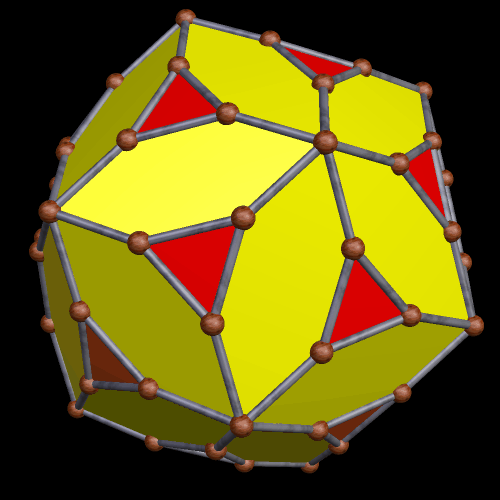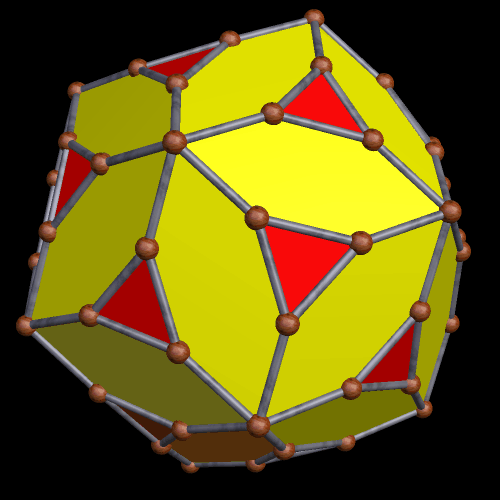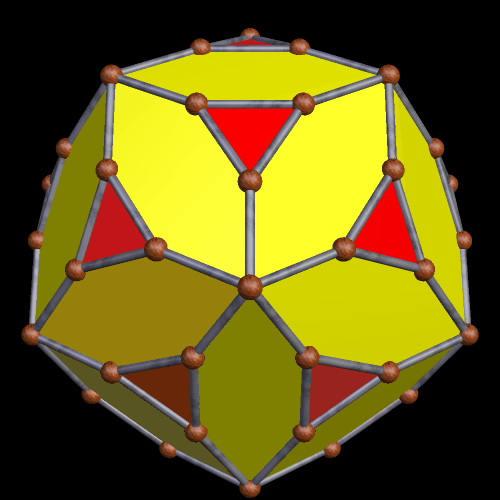
To begin this, I took an icosahedron, and made a zonish polyhedron with it, with the new faces based on the zones of the existing faces. Here’s the result.

Next, I started stellating the polyhedron above. At the sixth stellation, I found this. It’s a true zonohedron, and the first polyhedron shown here is merely “zonish,” because one has triangles, and the other does not. (One of the requirements for a polyhedron to be a zonohedron is that all its faces must have an even number of sides.)
 After that, I kept stellating, finding this as the 18th stellation of the first polyhedron shown here.
After that, I kept stellating, finding this as the 18th stellation of the first polyhedron shown here.

With this polyhedron, I then made its convex hull.
 At this point, the irregular hexagons were bothering me, so I used Stella 4d‘s “try to make faces regular” option. (Stella 4d is polyhedron-manipulation software you can try for free, or purchase, right here.)
At this point, the irregular hexagons were bothering me, so I used Stella 4d‘s “try to make faces regular” option. (Stella 4d is polyhedron-manipulation software you can try for free, or purchase, right here.)

The next step I chose was to augment all the yellow trapezoids with prisms, each with a height 1.6 times the trapezoids average edge length.
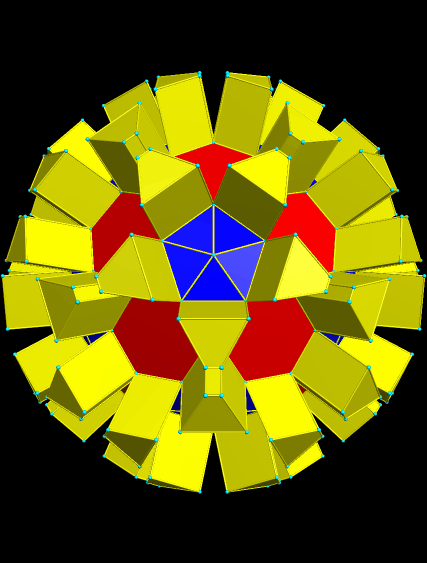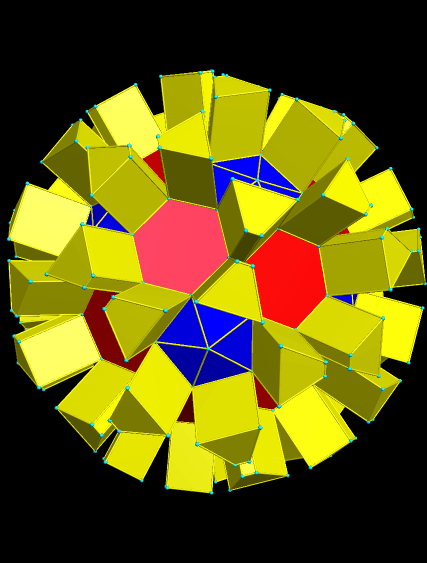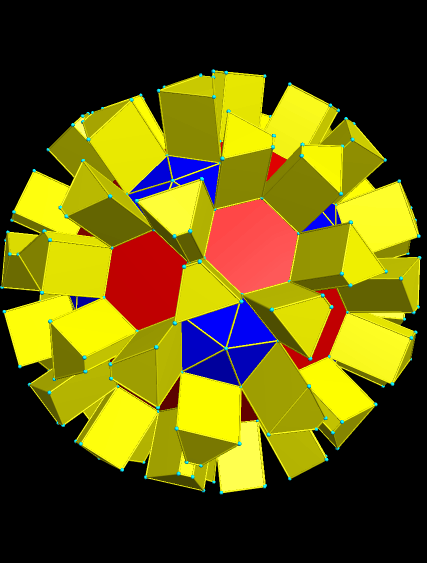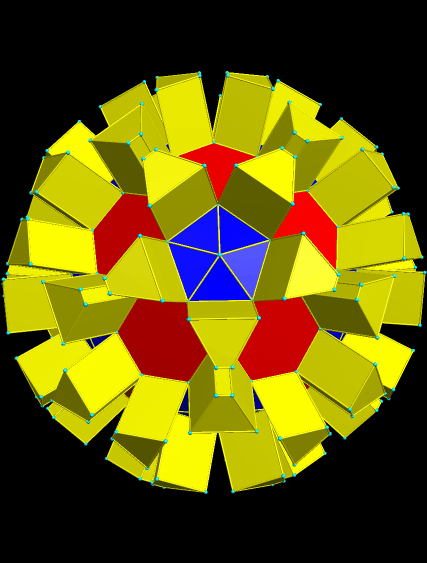
The next step was, again, to make the convex hull.
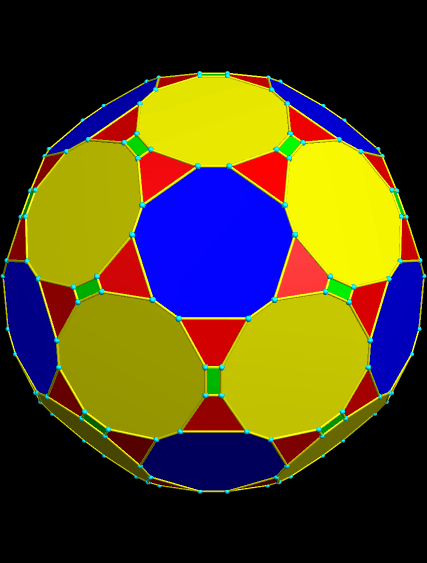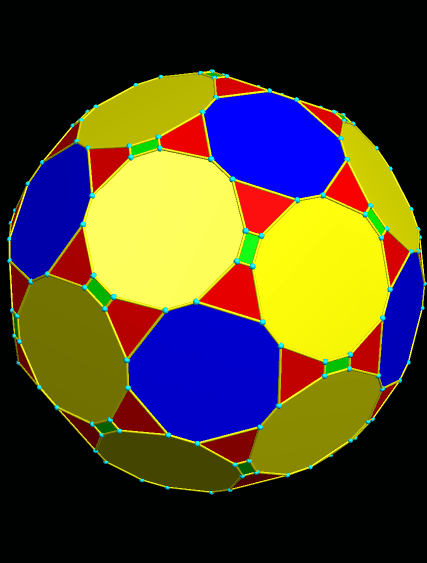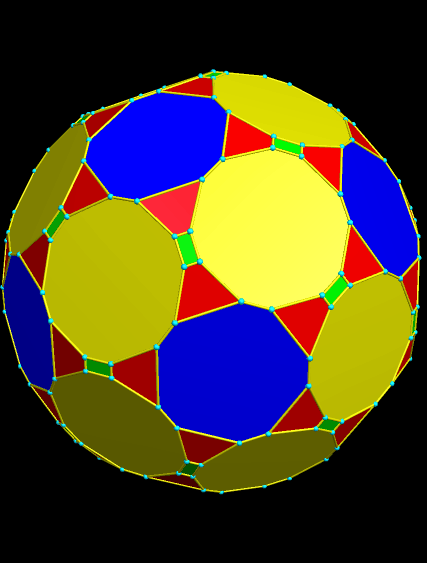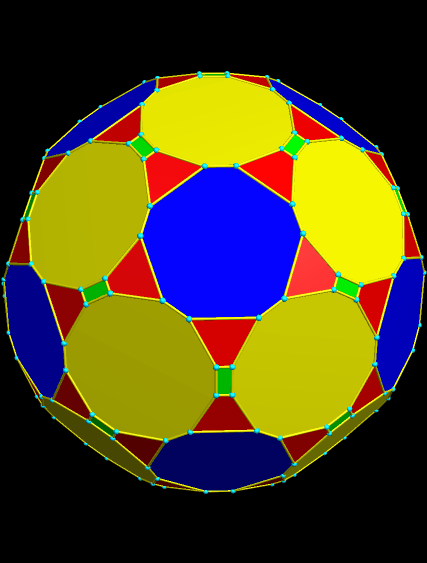
At this point, I tried “try to make faces regular” again, and was pleased with the result. The green rectangles became so thin, however, that I had to stop displaying the edges and vertices, in order for then to be seen.
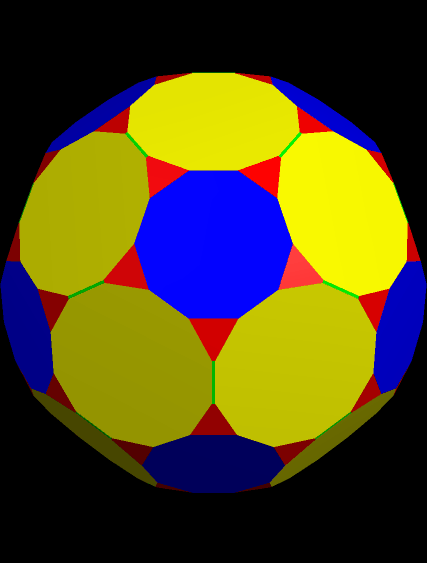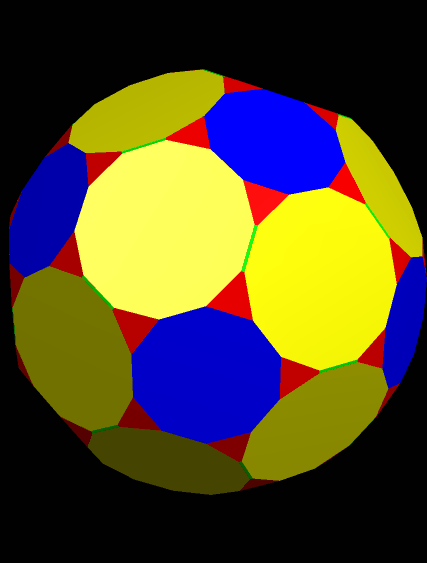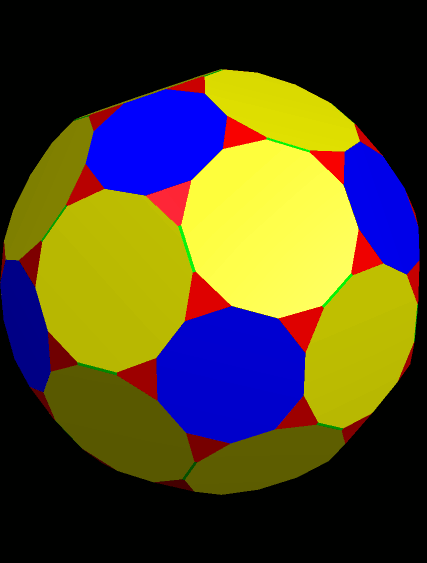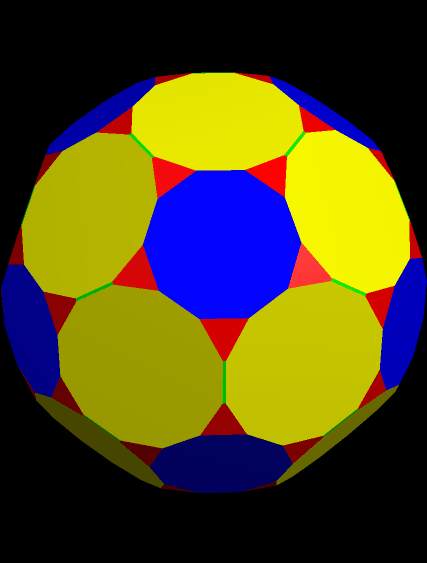 Next, I augmented both the blue faces (decagons) and the yellow faces (dodecagons) with antiprisms, again using a height 1.6 times that of the augmented faces’ average edge-lengths.
Next, I augmented both the blue faces (decagons) and the yellow faces (dodecagons) with antiprisms, again using a height 1.6 times that of the augmented faces’ average edge-lengths.

Next, I made the convex hull again — a step I often take immediately after augmenting a polyhedron.

This one surprised me, as it is more complicated than I expected. To clean things up a bit, I augmented only the trapezoids (dark pink) with prisms, and dodecagons (green) with antiprisms, again using the factor 1.6 for the augmentation-height.

The next step I chose was to take the convex hull, once more. I had not yet noticed that the greater height of the trapezoidal prisms would cause the dodecagonal antiprisms to be “lost” by this step, though.
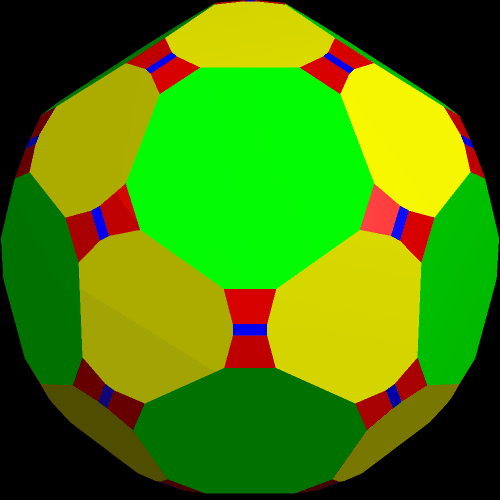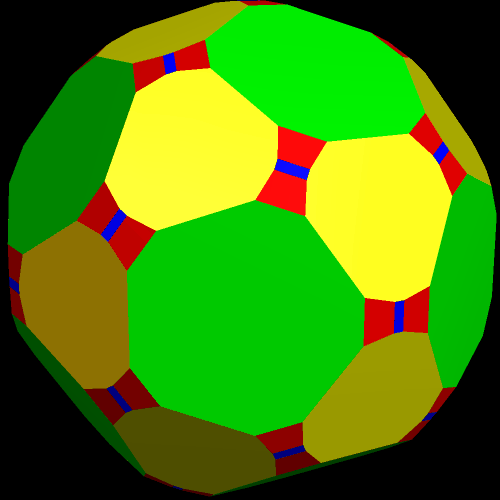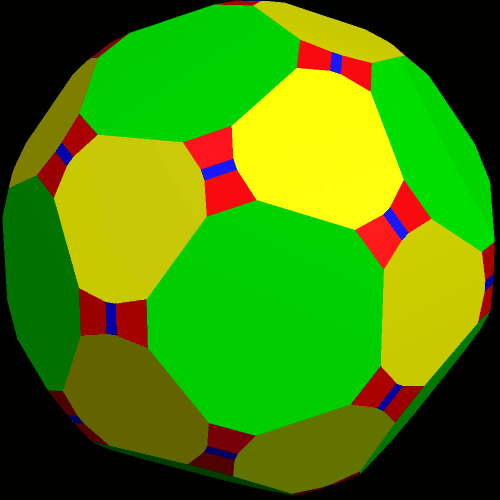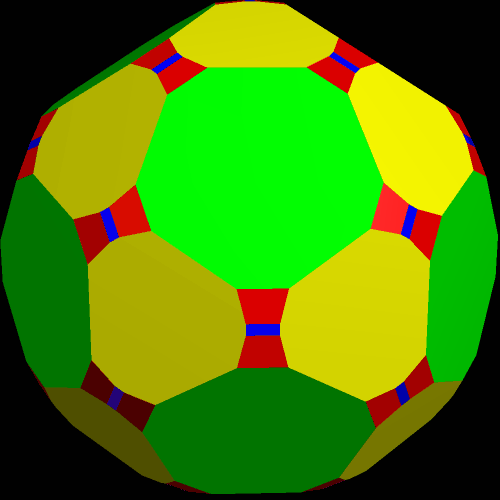
Next, “try to make faces regular” was used again.

This last result had me feeling my polyhedral journey was going in circles, so I tried augmentation again, but in a different way. I augmented this polyhedron, using prisms, on only the red trapezoids (height factor, 1.6 again) and the blue rectangles (new height factor, 2.3 times average edge length).
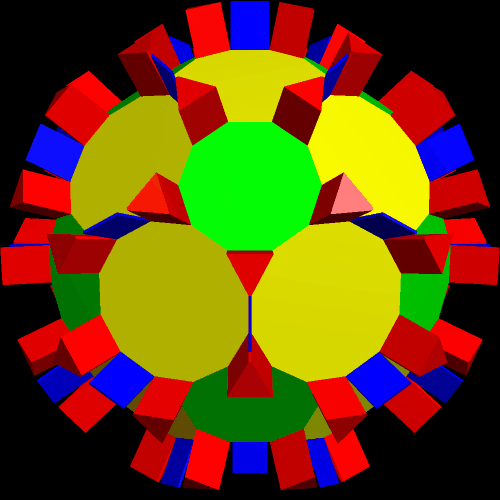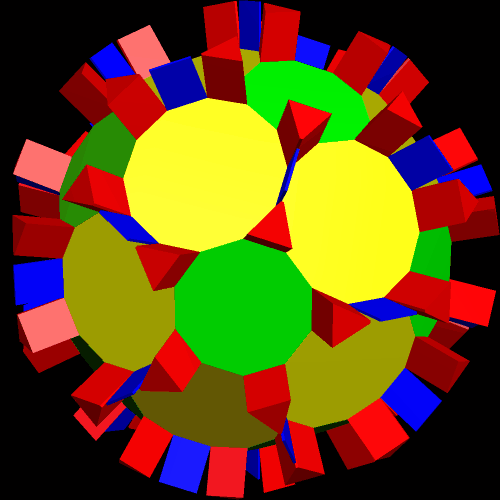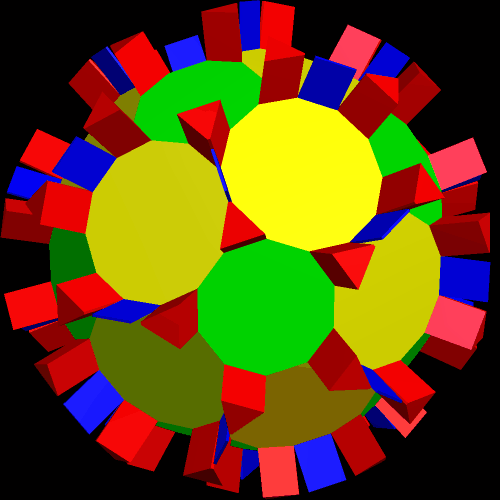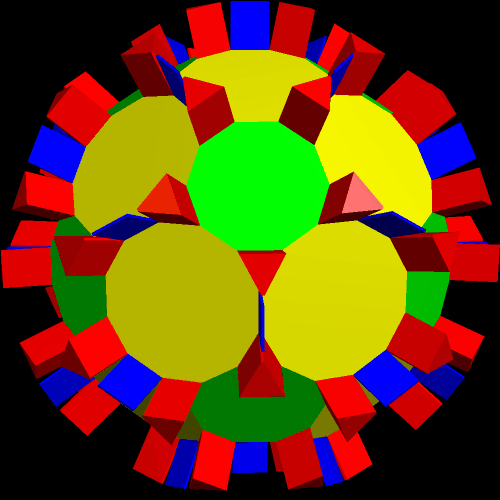
After that, it was time to make another convex hull — and that showed me that I had, indeed, taken a new path.
 I found the most interesting faces of this polyhedron to be the long, isosceles trapezoids, so I augmented them with prisms, ignoring the other faces, using the new height-factor of 2.3 times average edge length this time.
I found the most interesting faces of this polyhedron to be the long, isosceles trapezoids, so I augmented them with prisms, ignoring the other faces, using the new height-factor of 2.3 times average edge length this time.
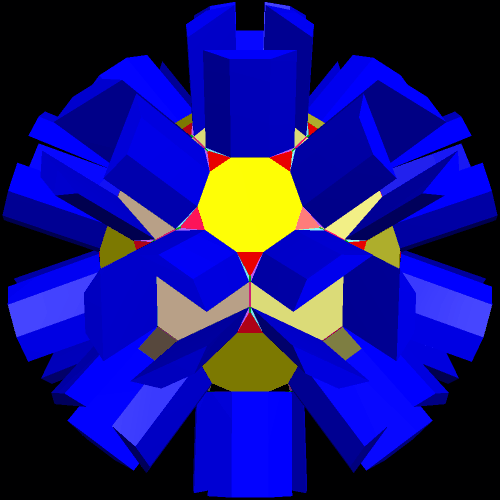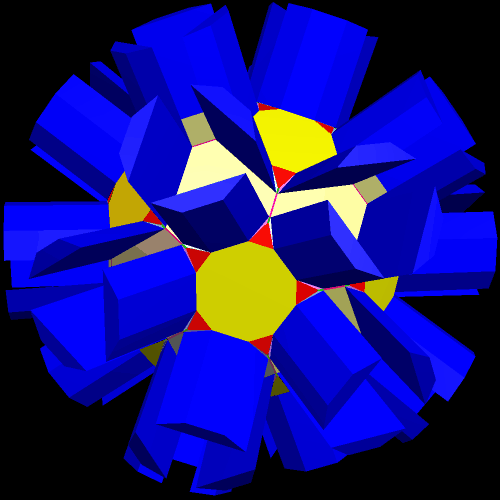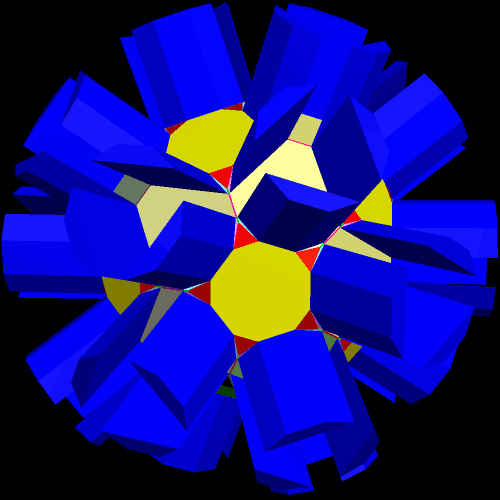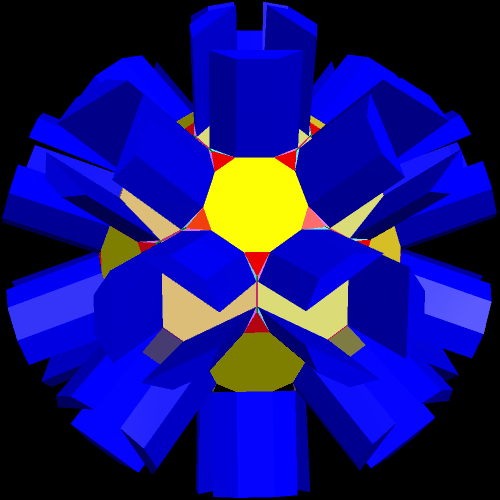
Of course, I wanted to see the convex hull of this. Who wouldn’t?

I then started to stellate this figure, choosing the 14th stellation as a good place to stop, and making the edges and vertices visible once more.