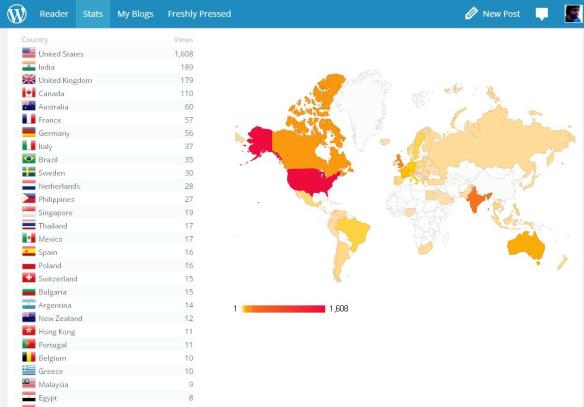
Since I’ve started blogging on WordPress, there have been several surprises, but the most puzzling to me is the recent rise in popularity of my blog in India. I live in the USA, so it’s no surprise that most hits on my blog come from here. However, I have no explanation for why India is #2.
This blog has a high math content, compared to most blogs. Might that have something to do with it?
Whatever the reason, I’m glad I have readers there.
The part of this map I don’t like involves China, Iran, and North Korea: zero hits from each nation. That has nothing to do with the content of my blog, of course, but with heavy censorship in each of those countries, all of which have notoriously bad human-rights records. In at least one of those nations (Iran), my blog has been read, but that doesn’t show up on this map because of the extreme lengths my friends in Iran have to go to simply to surf the web without detection and interference from Tehran.
I would like, someday, to visit all of these countries. In the cases of Iran, North Korea, and China, though, I’m waiting for regime changes first.