A Radial Tessellation of Regular Pentagons and Their Expanding Gap-Polygons

Posted on 10 August 2014 by RobertLovesPi

I call this sort of thing a “radial tessellation” — it follows definite rules that resemble those for regular or semi-regular tessellations, but possesses, primarily, radial symmetry. It also has lines of reflective symmetry, but these lines all meet at the radial-symmetry central point, which, in this case, is inside the central pentagon.

Moving out from the central point, the first gap-polygons encountered are black rhombi. The gaps exist because the 360 degrees necessary to surround a point cannot be divided by a whole number of 108 degree angles, from the regular pentagons, without leaving a remainder. This remainder, from arithmetic, is manifested geometrically as a gap between pentagons.

After the rhombi, moving further from the center, appear purple, non-convex equilateral hexadecagons, then, after that, larger, red polygons with more sides and indentations, and then the next, even-more-complex polygons after that, in yellow. Off the edges of the screen, this increase in gap-polygon size and complexity continues without limit, provided the pattern shown is followed. Here is the “recipe” for producing it:

1. Begin with a regular pentagon. Locate its center, and use it as the center point for all rotations.

2. Designate the line containing an outer edge of your figure as a line of reflection.

3. Reflect your entire figure over the designation line of reflection.

4. Take the newly-reflected figure, and rotate it around the central point by 72 degrees. Next, perform this same rotation, using the newest figure produced each time, three more times.

5. Return to step 2.

A Tessellation Using Regular Pentagons and Hexagons, As Well As Two Types of Concave Polygon

Posted on 10 August 2014 by RobertLovesPi

Without even checking, I know that my automatic tweet about this post (as @RobertLovesPi) will be retweeted by the @HexagonBot on Twitter. Why? Because @HexagonBot retweets any tweet containing the word “hexagon,” or “hexagons.” I have absolutely no idea why other polygons lack their own Twitterbots, though.

A Euclidean Construction of a Regular Pentagon with a Given Edge Length

Posted on 10 August 2014 by RobertLovesPi

The most well-known method for constructing a regular pentagon causes it to be inscribed in a given circle with a known center. It’s easy to find, on-line or in textbooks, and I will not be reproducing that construction here.

Because the diagonals and sides of a regular pentagon are in the golden ratio, it is also not difficult to construct a golden rectangle, and then use it to construct a regular pentagon. Given the ease of finding instructions for constructing a golden rectangle elsewhere, though, I’m not posting that construction here, either. This one begins with two distinct points, A and B, and the segment which connects them. The goal here is to start with only that, and then construct a regular pentagon, with sides of length AB, using only the methods permitted for Euclidean constructions.

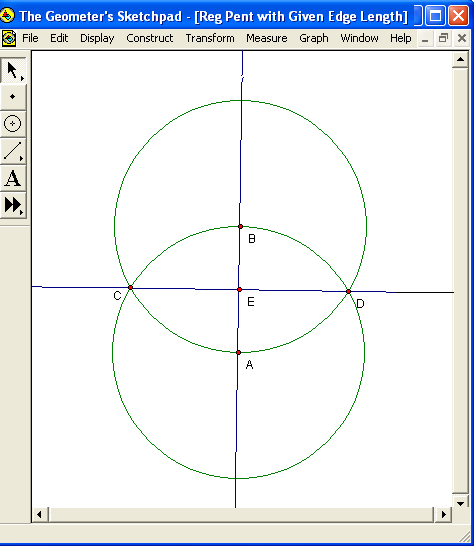
After segment AB has been drawn, the next step is to continue it, in both directions, to form line AB. Next, construct two circles, each with radius AB: one centered on A, and the other centered on B. These circles must intersect at two points, labeled C and D, as shown above. The next step is to construct line CD, and label, as point E, the intersection of lines AB and CD. This is the well-known procedure for constructing the perpendicular bisector of a segment, so E is the midpoint of segment AB, and the four angles with vertices at E are each right angles.

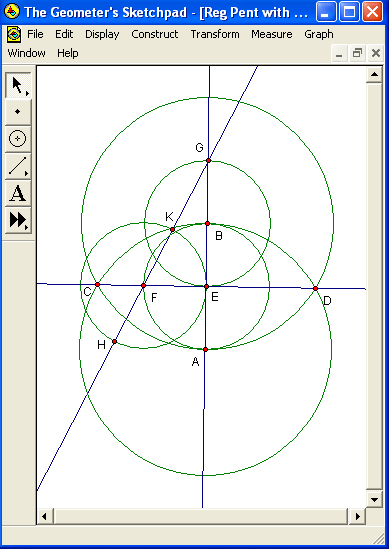
Next, construct a circle, centered on E, with radius AE. Label, as point F, the intersection of this circle with segment CE. After than, construct a circle, centered on B, with radius BE. This circle intersects line AB at two points, one of which is already labeled E. Label, as point G, the other such intersection. At this time, because they are all radii of equal-sized circles, the following lengths are equal: AE, BE, BG, and EF. Segment EG, however, is twice as long as any of these shorter and equal-length segments, since it is a straight segment formed by combining non-overlapping segments BE and BG. Since the same can be said for segment AB as well — its length equals AE + BE, or 2AE by substitution and addition — it follows that AB = EG. The next step is to construct line FG, which necessarily includes segment FG. Since segment FG is the hypotenuse of right triangle EFG, which has one leg (segment EG) which is twice as long as the other leg (segment EF), it follows, from the Pythagorean Theorem, that the distance FG is equal to the distance EF times the square root of five. Next, construct a circle which is centered at F, and has segment EF for a radius. Label the intersections of line FG, and this circle, as points H and K, as shown above, with K being the closer of the two to point G. Now there are two new segments, FH and FK, which, because they are radii of the same circle as segment EF, are each equal in length to segment EF, as well as to segments AE, BE, and GB, each of which were already shown to be equal in length to EF, and half as long as either of the equal-length segments EG and AB.

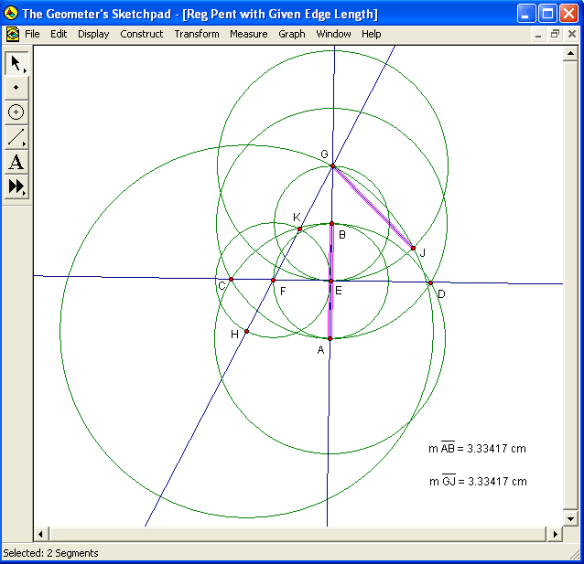
The next step is to construct a circle, centered at G, with radius EG. After that, consider the collinear and adjacent segments FH and FG, which, together, compose segment GH. FH is one of the several segments known to be half as long as AB, and FG’s length is already known to be equal to this shorter length (that of segments EF, FH, AE, etc.) times the square root of five. By the segment addition postulate, then, segment GH’s length is equal to the length of one of the shorter segments AE, EF, etc., times the sum of one and the square root of five. This length, GH, will be used as the diagonal-length of the regular pentagon, because GH’s length, and the edge length originally provided (AB), are in the golden ratio, since segment AB is twice as long as segment EF, and GH is equal to EF times the sum of one and the square root of five. GH is the radius of the next circle to construct, and that circle should be centered at H. This circle, the largest yet constructed, intersects the radius-EG circle centered at G at two points. One of these intersection-points, on the same side of line AB as right triangle EFG, need not be labeled, but the other one, on the other side of line AB, should be labeled as point J, as shown above. Segments GJ and EG, then, have equal lengths, for they are radii of the same circle — and the distance EG has already been shown to be equal to the distance AB, so GJ = AB as well. The segments GJ and AB are highlighted in pink in the diagram above, with their lengths shown, in order to provide additional evidence that their lengths are equal.

pent4

In the diagram above, segment GJ is shown in bold, because it is a side of the pentagon being constructed. Segment HJ is then constructed, and is also shown in bold, for it is a diagonal of that same pentagon, having the correct length by virtue of being a radius of the same circle as segment GH, which was already shown to have the correct length for a diagonal of the pentagon. The next step is to locate point L, which will be a vertex of the pentagon. To do that, construct a circle of radius HK, centered on H. Because segment HK is formed by the non-overlapping, adjacent, and collinear segments FH and FK, each of which has the same length as AE or AB, it follows that HK, the radius of the last circle constructed, is equal in length to both AB and GJ, with this distance being the side-length of the pentagon being constructed.

Next, construct a circle which has radius GH (the diagonal-length of the pentagon), and is centered at G. This circle, and the already-constructed circle with radius HK which is centered at H, intersect at two points. Label one of these points of intersection (the one on the same side of line AB as point J) as point L, as shown above, and then construct pentagon-sides HL and JL, also shown in bold in the figure above. (Also shown: measured lengths of all segments rendered in bold thus far, as well as AB.) Of these last two circle-intersection points, one has now been labeled as point L. The next step is to label the other such intersection as point M, as shown in the diagram below.

pent5

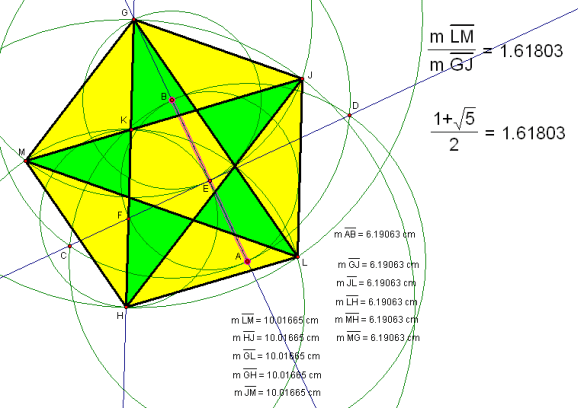
Once point M is located, the remaining sides and diagonals of regular pentagon GJLHM can be constructed, as shown above, in bold, simply by connecting each remaining unconnected pair of pentagon-vertices with a segment. The lengths of all bold segments, plus the original segment AB, are also shown above. As you can see, all five sides have length equal to the length of segment AB, while all five diagonals have a length greater than that of AB, but one which is constant throughout the set of diagonals.

In the diagram above, no new objects have been constructed using the Euclidean tools, but the pentagon has been given color, and a check of the diagonal-length to side-length ratio has been performed. As you can see, in the uppermost calculation, the decimal approximation for this distance-ratio is given as 1.61803. The same result is obtained, in the second calculation shown, when the sum of one, and the square root of five, is divided by two — and, since this is the definition of the golden ratio, obtaining the same result, for both of these calculations, provides supporting evidence for the validity of this construction.

To perform one more test of this construction — one only possible with a virtual compass and straightedge, such as Geometer’s Sketchpad, the one I used here — points A and/or B can be moved around. I chose to move them both, and I also increased the distance between them. As you can see, this increased all the side and diagonal lengths, as well as the length of the original segment, AB. However, segment AB still has the same length as all five pentagon sides. Also, all five diagonals, while they do have a longer length than any side, still have lengths equal to each other. Also, the diagonal-length to side-length ratio remains constant, at the value of the golden ratio, even though the actual distances all changed when A and B were moved. The construction, and its explanation, are now complete.

Octahedral Cluster of 104 Unit Cubes

Posted on 9 August 2014 by RobertLovesPi

This is not hollow — the 104 cubes here include those hidden from view inside this octahedral cluster, as well as the ones you can see.

Software used to make this image: Stella 4d, available at www.software3d.com/Stella.php.

A Graph Showing Approximate Mass-Boundaries Between Planets, Brown Dwarfs, and Red Dwarf Stars

Posted on 9 August 2014 by RobertLovesPi

I found the data for this graph from a variety of Internet sources, and it is based on a mixture of observational data, as well as theoretical work, produced by astronomers and astrophysicists. The mass-cutoff boundaries I used are approximate, and likely to be somewhat “fuzzy” as well, for other factors, such as chemical composition, age, and temperature (not mass alone), also play a role in the determination of category for individual objects in space.

Also, the mass range for red dwarf stars goes much higher than the top of this graph, as implied by the thick black arrows at the top of the chart. The most massive red dwarfs have approximately 50% of the mass of the Sun, or about 520 Jovian masses.

Proposed Mechanisms for New and Different Types of Novae

Posted on 9 August 2014 by RobertLovesPi

The picture above shows a proposed model for the production of a sudden increase in the brightness of a star — or rather, what is apparently a single star, optically, but would actually be a suddenly-produced binary stellar system.

The yellow object is a star, the system’s primary, and it has high mass (at least a few solar masses), when its mass is compared to those of the brown dwarfs in the two highly elliptical orbits shown in blue. These brown dwarfs aren’t quite stars, lacking enough mass to fuse hydrogen-1, which requires 75 to 80 Jupiter masses, but one of them (the larger one) is close to that limit. The smaller brown dwarf has perhaps half the mass of the larger brown dwarf. Their high orbital eccentricities give them very long orbital periods, on the order or 100,000 years. In a very small fraction of orbits, both brown dwarfs will be near perihelion (closest point to the primary) at the same time, and, during those rare periods, the two brown dwarfs become much closer to each other than they are to the primary.

When the two brown dwarfs become close enough to each other, matter from the smaller one could be drawn, by gravity, into the larger brown dwarf, increasing its mass, at the expense of its smaller sibling. At some point, in such a system, the larger brown dwarf’s mass could then reach the threshold to begin fusing hydrogen-1, and “turn on” as a true star — a red dwarf. From Earth, this red dwarf would not be distinguishable from the system’s most massive star, shown in yellow, until much later, when the two moved further apart. There would, however, be a sudden increase in luminosity from the system as a whole. Unlike other types of novae, this increase in luminosity would not fade away quickly, for red dwarfs have very long lifespans. This would enable them, upon discovery, to be distinguished from other single-brightening stellar events. Confirmation could then come from resolution of the new red dwarf component, as it recedes from the primary, making detection easier.

For a variation on this mechanism, the primary star could be somewhat more massive, and the two large brown dwarfs could be replaced by two large red dwarf stars. The larger red dwarf could draw matter from the smaller one, until the larger red dwarf became large enough to cross a higher mass threshold, and brighten substantially, with its color suddenly changing to orange or yellow.

A problem for this model: no such events are known to have happened. If they do happen, a likely explanation for their rarity is the likelihood that such orbits would be unstable, in a large fraction of similar cases, preventing the stellar-brightening event from having time to happen — in all but a few cases, none of which humans have (yet) both seen, and understood. If one of these things goes off nearby, though, we will learn about it quickly, for it will make itself known.

For another possible mechanism, there is another option: remove the primary altogether, and let the two objects of near-threshold mass orbit their common center of mass directly. They could then create a new star, or brighter star, by the mechanism described, one which might even produce a detectable accretion disk. A actual merger of the two brown dwarfs, or red dwarf stars, would be a variation of this idea, and would presumably be more likely if the two objects had masses very close to each other, so that neither would have an advantage in the gravitational tug-of-war.

Public Schools in the United States Should Rename the “Free Lunch”

Posted on 8 August 2014 by RobertLovesPi

If you live in the USA, you are probably familiar with the phrase “free lunch,” or “free and reduced lunch,” as used in a public-school context. For those outside the USA, though, an explanation of what that phrase means, in practice, may be helpful, before I explain why a different name for such lunches should be used.

The term “free and reduced lunch” originated with a federal program which pays for school lunches, as well as breakfasts, with money collected from taxpayers — for students whose families might otherwise be unable afford these meals. The program’s eligibility requirements take into account both family income and size. There’s a problem with it, though: the inaccuracy of the wording used, especially the troublesome word “free.” The acronym above, “TANSTAAFL,” is familiar to millions, from the works of Robert A. Heinlein (science fiction author), Milton Friedman (Nobel-Prize-winning economist), and others. It stands for the informally-worded phrase, “There ain’t no such thing as a free lunch,” which gets to the heart of the problem with the terminology we use when discussing school lunches. (Incidentally, I have seen an economics textbook use the phrase “TINSTAAFL,” in its place, to change “ain’t no” to “is no.” I do not use this version, though, for I am unwilling to correct the grammar of a Nobel laureate.)

The principle that “free lunches” simply do not exist is an important concept in both physics and economics, as well as other fields. In physics, we usually call it the Law of Conservation of Mass and Energy, or the First Law of Thermodynamics. This physical law has numerous applications, and has been key to many important discoveries. Learning to understand it, deeply, is an essential step in the education of anyone learning physics. Those who teach the subject, as I have in many past years, have an even more difficult task: helping students reach the point where they can independently apply the TANSTAAFL principle to numerous different situations, in order to solve problems, and conduct investigations in the laboratory. It is a fundamental statement of how the universe works: one cannot get something for nothing.

TANSTAAFL applies equally well in economics, where it is related to such things as the fact that everything has a cost, and those costs, while they can be shifted, cannot be made to simply disappear. It is also related to the principle that intervention by governments in the economy always carries costs. For example, Congress could, hypothetically, raise the federal minimum wage to $10 per hour — but the cost of doing so would be increased unemployment, especially for those who now have low-paying jobs. Another possible cost of a minimum-wake hike this large would be a sudden spike in the rate of inflation, which would be harmful to almost everyone.

To understand what people have discovered about the fundamental nature of physical reality, physics must be studied. To understand what is known about social reality in the modern world, economics must be studied. Both subjects are important, and understanding the TANSTAAFL principle is vital in both fields. Unfortunately, gaining that understanding has been made more difficult, for those educated in the United States, simply because of repeated and early exposure to the term “free lunch,” from childhood through high school graduation. How can we effectively teach high school and college students that there are no free lunches, when they have already been told, incessantly, for many years, that such things do exist? The answer is that, in many cases, we actually can’t — until we have first helped our students unlearn this previously-learned falsehood, for it stands in the way of the understanding they need. It isn’t a sound educational practice to do anything which makes it necessary for our students to unlearn untrue statements.

I am not advocating abolition, nor even reduction, of this federal program, which provides essential assistance for many families who need the help. Because I am an American taxpayer, in fact, I directly participate in funding this program, and do not object to doing so. I do take issue, however, with this program teaching students, especially young, impressionable children in elementary school, something which is untrue.

We need to correct this, and the solution is simple: call these school lunches what they actually are. They aren’t free, for we, the taxpayers, pay for them. Nothing is free. We should immediately replace the phrase “free and reduced lunch” with the phrase “taxpayer-subsidized lunch.” The second phrase is accurate. It tells the truth, but the first phrase does the opposite. No valid reason exists to try to hide this truth.

7511

Posted on 7 August 2014 by RobertLovesPi

“A thought is an idea in transit.” ~Pythagoras, quoted on a moving rhombic dodecahedron

Posted on 7 August 2014 by RobertLovesPi

Rhombic Dodeca

Created using Stella 4d, available at www.software3d.com/Stella.php.

A Non-Convex Polyhedron with Sixty Non-Convex Pentagonal Faces

Posted on 7 August 2014 by RobertLovesPi

Created using Stella 4d: Polyhedron Navigator, available for purchase (with a free trial download available, first) at www.software3d.com/Stella.php.