Icosagons are polygons with twenty sides, and do not appear in any well-known polyhedra. The first of these three regular-icosagon-based polyhedra has 122 faces.
The second of these polyhedra, each of which bears an overall resemblance to a dodecahedron, has 132 faces.
Finally, the third of these polyhedra has a total of 152 faces.
I used Stella 4d to make each of these virtual polyhedron models — and you may try this program for free at http://www.software3d.com/Stella.php.
In the last post here, there were two polyhedra shown, and the second one included faces with nine sides (enneagons, also known as nonagons), as well as fifteen sides (pentadecagons), but those faces were not regular.
The program I use to manipulate polyhedra, Stella 4d (available at http://www.software3d.com/Stella.php), has a “try to make faces regular” function included. When I applied it to that last polyhedron, in the post before this one, Stella was able to make the twenty enneagons and twelve pentadecagons regular. The quadrilaterals are still irregular, but only because squares simply won’t work to close the gaps of a polyhedron containing twenty regular enneagons and twelve regular pentadecagons. These quadrilaterals are grouped into thirty panels of four each, so there are (4)(30) = 120 of them. Added to the twelve pentadecagons and twenty enneagons, this gives a total of 152 faces for this polyhedron.
It would really be a pain to count the faces of this polyhedron, in order to verify that there are 270 of them. Fortunately, it isn’t necessary to do so. The polyhedron above is made of rhombus-shaped panels which correspond to the thirty faces of the rhombic triacontahedron. Each of these panels contains nine faces: one square, surrounded by eight triangles. Since (9)(30) = 270, it is therefore possible to see that this polyehdron has 270 faces, without actually going to the trouble to count them, one at a time.
The software I used to make this polyhedron may be found at http://www.software3d.com/Stella.php, and is called Stella 4d. With Stella 4d, a single mouse-click will let you see the dual of a polyhedron. Here’s the dual of the one above.
This polyhedron is unusual, in that it has faces with nine sides (enneagons, or nonagons), as well as fifteen sides (pentadecagons). However, these enneagons and pentadecagons aren’t regular — yet — but they will be in the next post.
The Platonic solid known as the icosahedron has twenty triangular faces. This polyhedron resembles the icosahedron, but with each of the icosahedron’s triangles replaced by a panel of four faces: three isosceles trapezoids surrounding a central triangle. Since (20)(4) = 80, it is possible to know that this polyhedron has eighty faces — without actually counting them.
To let you see the interior structure of this figure, I next rendered its triangular faces invisible, to form “windows,” and then, just for fun, put the remaining figure in “rainbow color mode.”
I perform these manipulations of polyhedra using software called Stella 4d. If you’d like to try this program for yourself, the website to visit for a free trial download is http://www.software3d.com/Stella.php.
Something I have in common with the fictional Captain Kirk, from the original Star Trek series, is that I enjoy playing both poker and chess. In the scene depicted above, from the episode “The Corbomite Maneuver,” the Enterprise is facing an adversary who dramatically outpowers them — and Kirk escapes the situation with an outrageous bluff, right after making this reference to the game of poker.
Unlike Captain Kirk, however, I am not skilled at bluffing, with two consequences: (1) I’m a terrible poker player, and (2) I do not attempt bluffing as a strategy, unless I am actually playing poker.
I’ve been an activist for a large variety of causes, for decades, and, because of this activism, have acquired a rather large number of adversaries. Many of them have figured out that I don’t bluff, but some — rather surprisingly, considering they have known me for years — have not. The amusing thing, to me, is that I’ve always been quite open about this, but some still fail to realize it, despite my candor on the subject. When engaged in any struggle, I only make statements I believe to be true, for one simple reason: I’m so terrible at bluffing, or other forms of lying, that any untrue statement I were to make would be instantly recognized as dishonest. Since I figured this out, about myself, decades ago, I deliberately choose to only employ strategies which are completely honest. It would be stupid, after all, for me to employ strategies with which I know I have weak skills.
So, unless I’m actually playing real poker, and am engaged in any sort of struggle, I’m basically playing metaphorical chess. This involves figuring out what my opponents are thinking, devising strategies to counter theirs, and remaining at least three moves ahead of my adversaries, at all times. I’m far more like Mr. Spock than I am like Captain Kirk, and always have been. This isn’t going to change.
I find it hilarious that I can post these absolutely-true statements right here, on the Internet, where anyone can see them — and have full confidence that those who persist in their mistaken belief that I’m bluffing, about anything, will continue to make this enormous error in judgment — until it’s too late. For them, that is.
If one starts with a single icosidodecahedron, and then augments its pentagonal faces with dodecahedra, and its trianguar faces with icosahedra, this is the result.
This figure has gaps in it where two pentagons and two triangles meet around a vertex. If one puts icosidodecahedra in those gaps, this is the resulting figure.
Next, once again, the pentagonal faces are augmented with dodecahedra, and the triangular faces with icosahedra.
These virtual polyhedral models were all built using Stella 4d, available at http://www.software3d.com/Stella.php.
It is well-known that the cuboctahedron and the rhombic dodecahedron are dual polyhedra. However, until I stumbled upon this, I was unaware that rhombic dodecahedra could actually be arranged into a cluster with the overall shape of a cuboctahedron.
[Software credit: see http://www.software3d.com/Stella.php for more information about Stella 4d, the program I use to make these rotating images. A free trial download is available at that website.]
One of the thirteen rhombic dodecahedra in this cluster cannot be seen, for it is hidden in the middle. The other twelve are each attached to a face of the central rhombic dodecahedron.
If one then creates the convex hull of this cluster — the smallest convex polyhedron which can contain it — this is the result:
This polyhedron has fifty faces: the six square faces of a cube, the eight triangular faces of an octahedron, the twelve rhombic faces of a rhombic dodecahedron, and twenty-four rectangles to fill the gaps between the other faces.
This fifty-faced polyhedron also has an interesting dual, with 48 faces, all of which are kites. Half of these 48 kites are of one type, and arranged into eight panels of three kites each, while the other half are arranged into six panels of four kites each:
Returning to the fifty-faced polyhedron, two images above, here is what happens if one tries to make each face as regular as possible:
In this polyhedron, the six squares are still squares, the eight triangles are still regular, and the twelve rhombi are still rhombi, although these rhombi are wider than before. The 24 rectangles, however, have now been transformed into isosceles trapezoids.
[Software credit: see http://www.software3d.com/Stella.php for more information about Stella 4d, the program I use to make these rotating images. A free trial download is available at that website.]
I’m going to start this experiment with a single octahedron, with faces in two colors, placed so that two faces which share an edge are always of different colors.
Next, I will augment the red faces — and only the red faces — with identical octahedra.
The regions with four blue, adjacent faces look as though they might hold icosahedra — but I checked, and they don’t quite fit. I will therefore continue the same process — augmenting only the red faces with more octahedra of the original type.
I’ve now decided that I definitely like this game, so I’ll keep playing it.
Immediately above, at the fourth of these images, some of the octahedra have started to overlap slightly, but I’m choosing to not be bothered by that — I’m continuing the now-established pattern, just in order to see where it takes me.
The regions of overlap are now far more obvious, but I’m continuing, anyway. Why? Because this is fun, that’s why! Right now, Stella 4d, the program I use to do these polyhedral manipulations, is chugging away on the next one. (This program is avilable at http://www.software3.com/Stella.php.) Ah, it’s ready — here it is!
Rather than repeat this process again, I now have another question: what would the convex hull of this figure look like? (A convex hull of a non-convex polyhedron is the smallest convex polyhedron which can contain a given non-convex polyhedron.) With Stella 4d, that’s easily answered.
I must admit this: that was nothing like what I expected — but such unexpected discoveries are a large part of what makes these polyhedral investigations with Stella 4d so much fun. And now, to close this particular polyhedral journey, I will have Stella 4d produce, for me, the dual of the convex hull shown above. (In case you aren’t familiar with duality regarding polyhedra, it describes the relationship between the octahedron, with which this post began, and the familar cube. Basically, with duals, faces and verticies are “flipped” over edges, although that is an extremely informal and imprecise way to describe the at the process.)
And with that, my friends, I bid you good night!
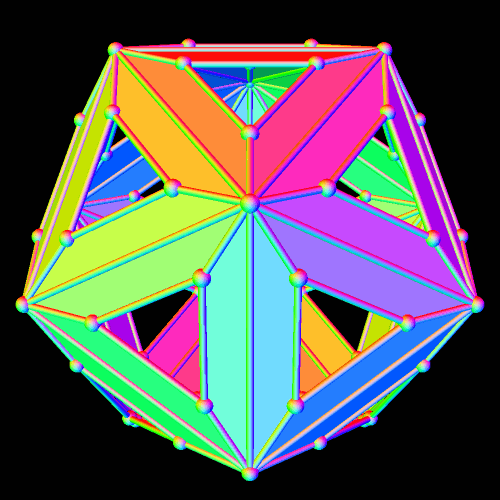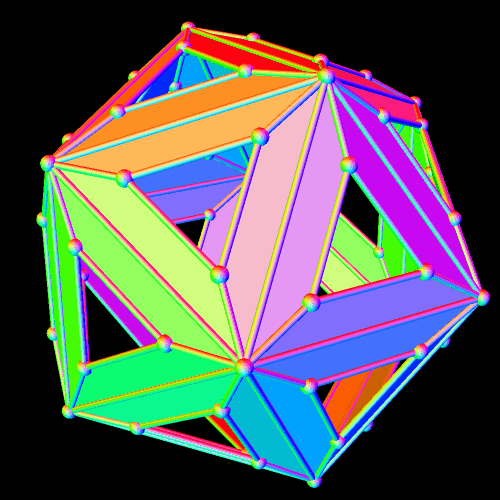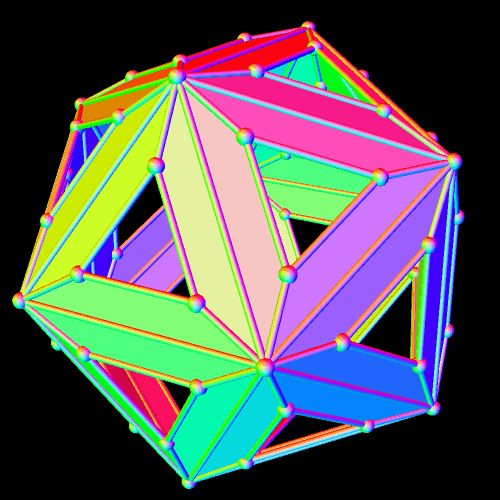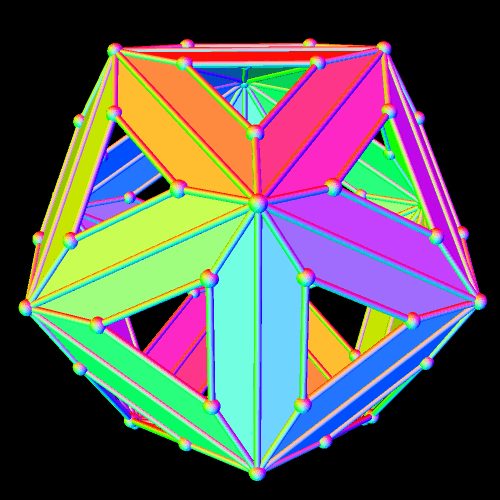
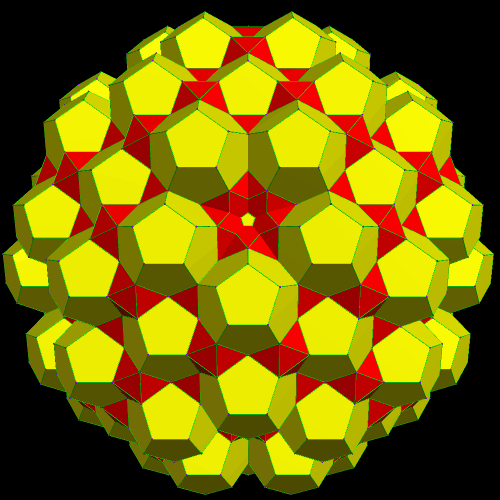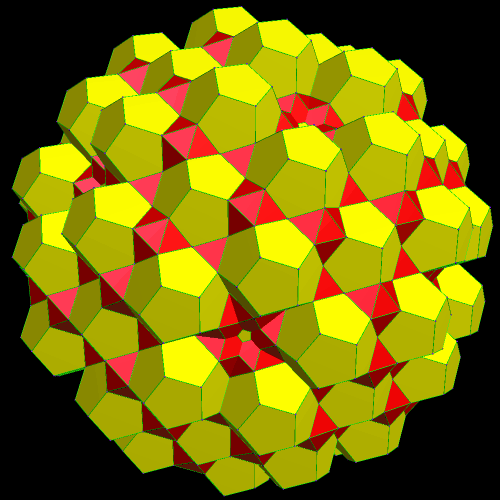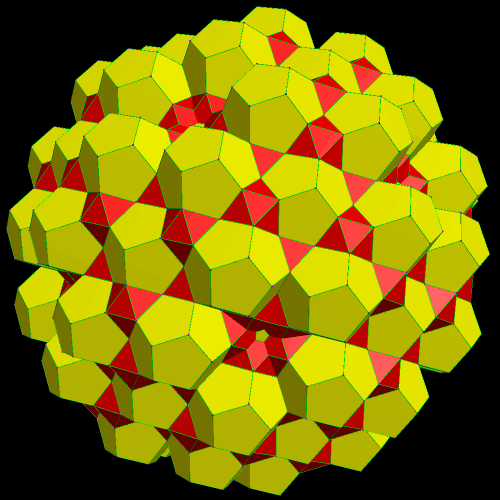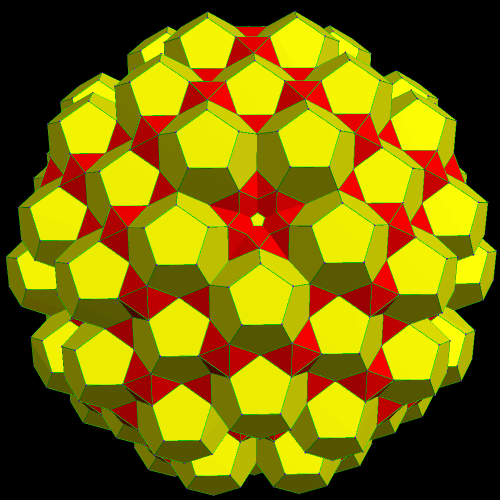
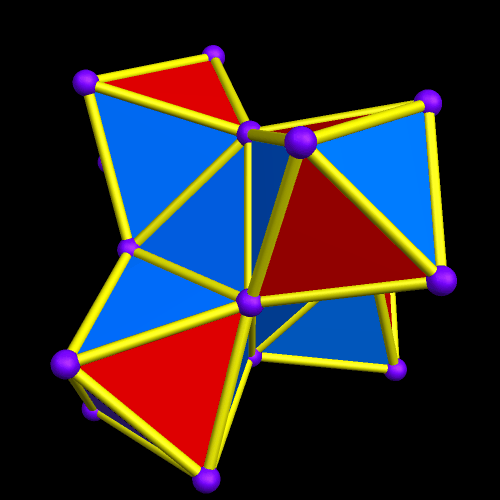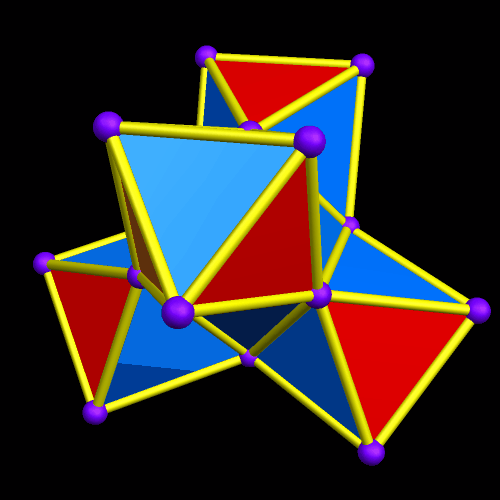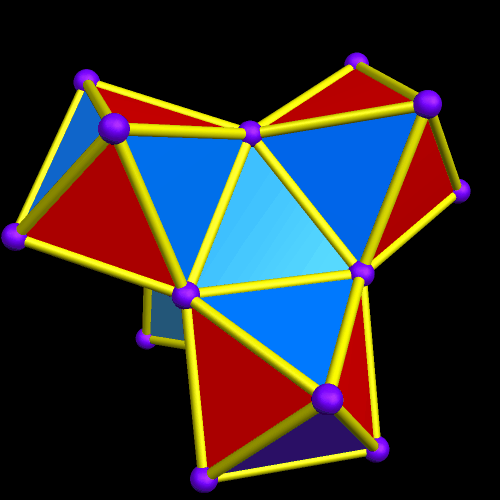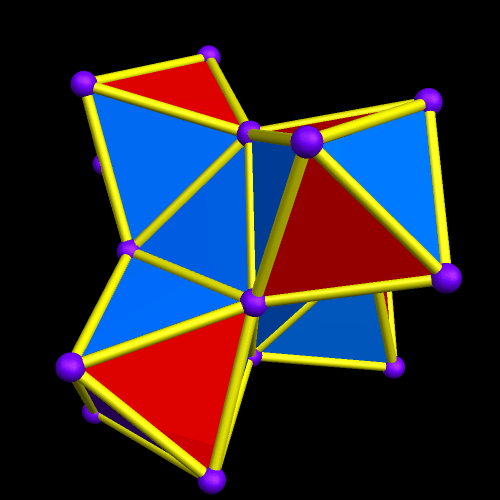
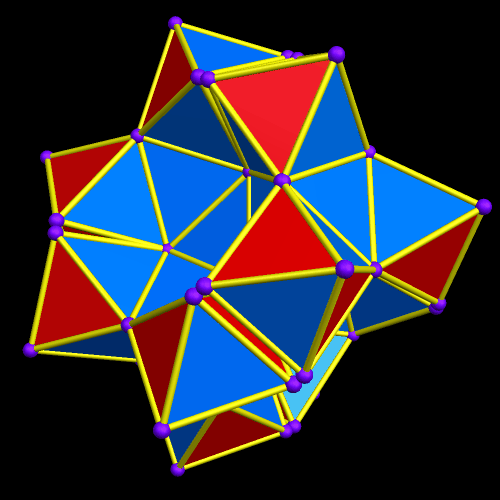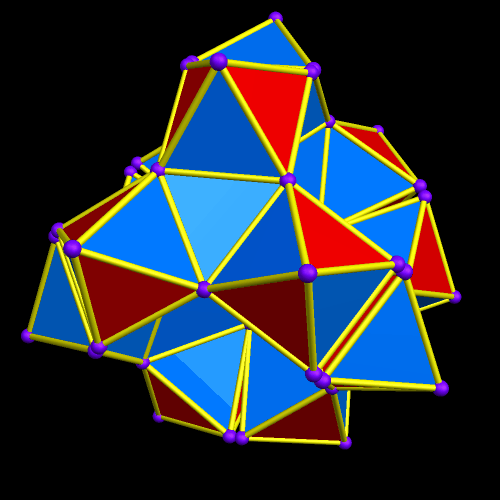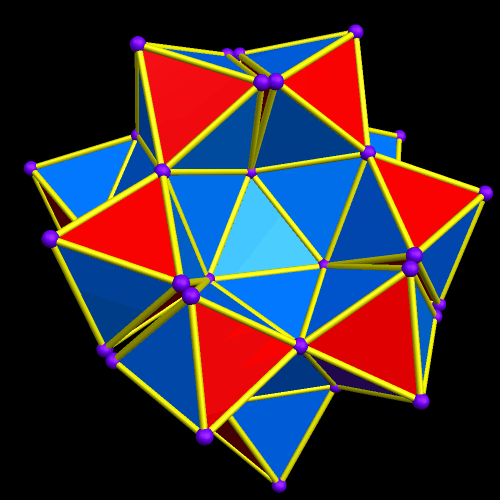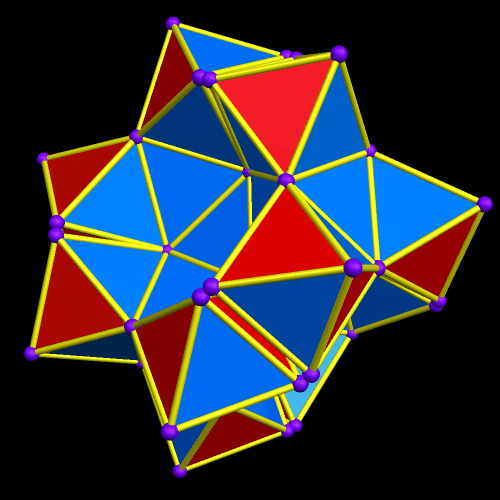
To build an octahedral lattice of rhombic triacontahedra, start with a single rhombic triacontahedron.
Next, augment its faces with more rhombic triacontahedra — but not all thirty faces. Instead, only augment six of them — the six which lie along mutually-perpendicular x-, y-, and z-axes. Another way to look at this is that you only augment the North, South, East, West, top, and bottom faces.
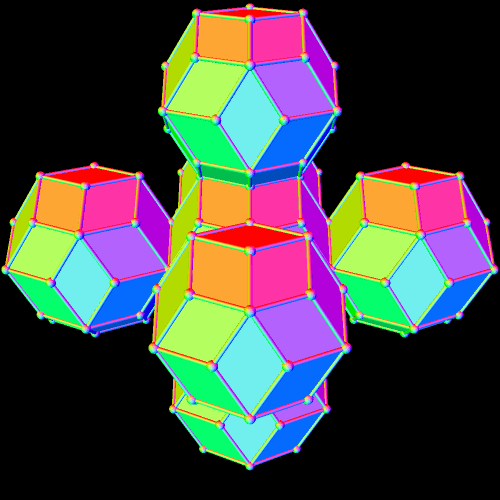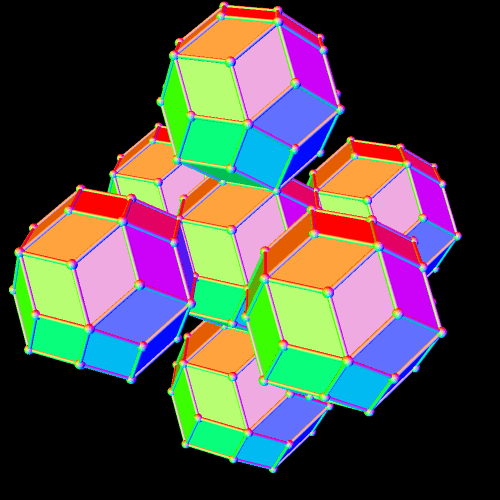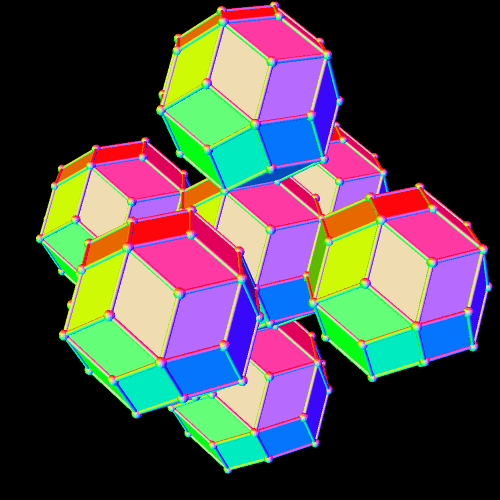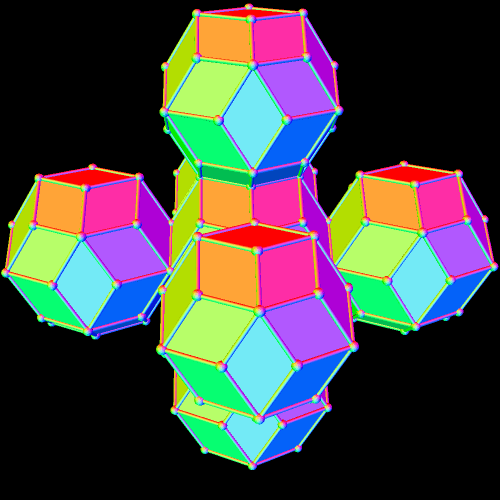
There are now seven rhombic triacontahedra in this small lattice, and one can begin to see the octahedral structure which is forming. The next step is to perform the same type of augmentation on each of the rhombic triacontahedra which exist at this point.
The overall octahedral shape of this lattice is now quite obvious. Also, there is one rhombic triacontahedron in the center, six in the layer next to the center, and eighteen in the outer layer, for a total of 1 + 6 + 18 = 25 rhombic triacontahedra, in the third of these figures, immediately above.
This latest augmentation increases the number of rhombic triacontahedra in the cluster by 38, for a total of 25 + 38 = 63 rhombic triacontahedra in the lattice shown immediately above. This pattern can, of course, be continued indefinitely — and, as it increases, the overall octahedral shape of the lattice becomes progressively more clear.
At this point, the 5th in the sequence, the number of new triacontahedra added, in the outermost layer, becomes more difficult to count, but it is certainly possible. In the middle level of this outermost layer, there are sixteen new triacontahedra. In the levels above and below that, there are twelve new rhombic triacontahedra, each. The next levels up and down contain eight more, each. Above and below those two levels, there are four each — and going one more step up and down takes one to the top, with one rhombic triacontahedron at the top, plus one more at the bottom. The number of new rhombic triacontahedra is, therefore, 16 + 12 + 12 + 8 + 8 + 4 + 4 + 1 + 1, which equals 66. Add 66 more (on the outside) to the 63 already inside, and you have the total number of rhombic triacontahedra in this latest lattice: 129.
The number of rhombic triacontahedra at each point in this series of geometric shapes is, itself, interesting. Here’s what we have so far.
Here is the next octahedral lattice of rhombic triacontahedra, with n = 6.
Now, at n = 6, this sum of the number of cells is (1) + (4 + 1 + 1) + (8 + 4 + 4 + 1 + 1) + (12 + 8 + 8 + 4 + 4 + 1 + 1) + (16 + 12 + 12 + 8 + 8 + 4 + 4 + 1 + 1) + (20 + 16 + 16 + 12 + 12 + 8 + 8 + 4 + 4 + 1 + 1) = 1 + 6 + 18 + 38 + 66 + 102 = 129 interior cells + 102 exterior cells = 231 cells, total. This also equals 11(1) + 9(4) + 7(8) + 5(12) + 3(16) + 1(20), which can also be written as 11 + 36 + 56 + 60 + 48 + 20. In terms of n, when n = 6, 11 + 36 + 56 + 60 + 48 + 20 may also be written as (2n – 1)(1) + (2n – 3)[4(n – 5)] + (2n – 5)[4(n – 4)] + (2n – 7)[4(n – 3)] + (2n – 9)[4(n – 2)] + (2n – 11)[4(n – 1)].
Obviously, I am trying to find a way to express the number of cells in the nth figure, in terms of n, but with only limited success, so far. The first six terms are 1, 7, 25, 63, 129, 231, and patterns of numbers above could easily be used to predict the seventh term, but that’s not my goal. What I want is a simple formula which will give me the total number of cells, in terms of n, for the nth of these octahedral lattices of rhombic triacontahedra. I’ll go ahead and find the seventh term, though, in the hope that it will help me figure out the pattern. When n = 7, the total number of cells will equal 13(1) + 11(4) + 9(8) + 7(12) + 5(16) + 3(20) + 1(24) = 13 + 44 + 72 + 84 + 80 + 60 + 24 = 377. Having found that number, I might as well throw in another picture, also. Stella 4d: Polyhedron Navigator, makes these rotating images easy to make, and you can try that program’s trial version for free, or purchase the fully-functioning version I use, at http://www.software3d.com/Stella.php.
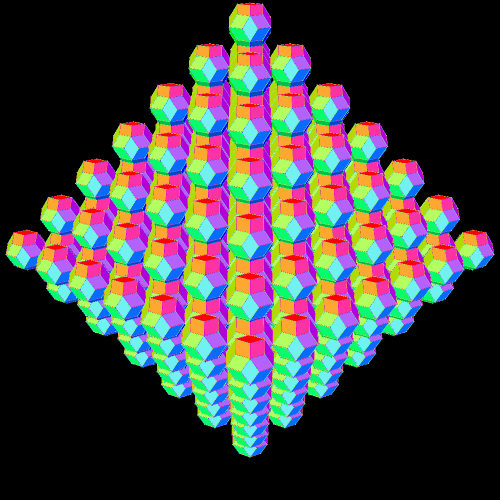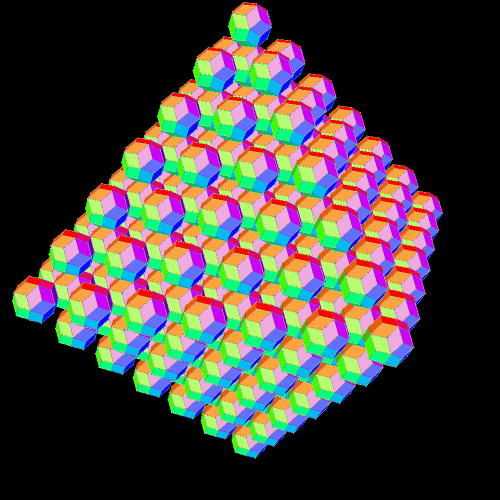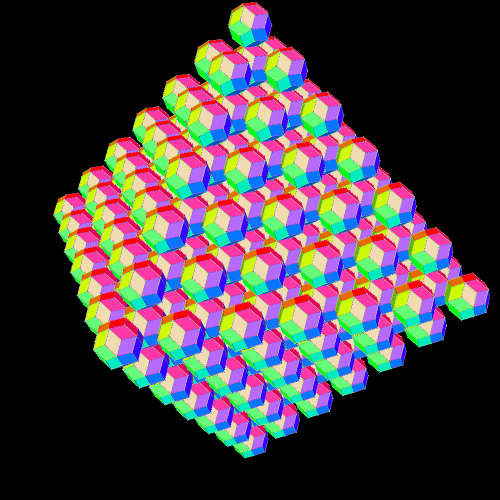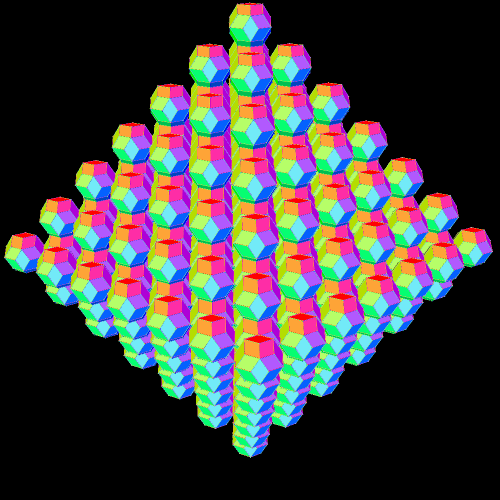
This did help: it helped me avoid a dead end (later edit: or so I thought). I had noticed that the first six terms (1, 7, 25, 63, 129, 231) stayed close to, or matched exactly, the cubes of the first six counting numbers (1, 8, 27, 64, 125, 216), with only the sixth term deviating far from the sixth perfect cube. With the seventh term, 377, the deviation from the seventh perfect cube, 343, grows even wider, so, at this point, I don’t think the solution is related to perfect cubes in any way. (However, please keep reading; sometimes things which appear to be mathematical dead ends are actually only illusions of dead ends.)
I’m not yet willing to give up, though. I will next analyze the differences in successive terms, the differences between those differences, and so on. For this, the eighth term might be helpful, so I’ll go ahead and find it. From one of the patterns above, I can see that the 8th term will equal 15(1) + 13(4) + 11(8) + 9(12) + 7(16) + 5(20) + 3(24) + 1(28) = 15 + 52 + 88 + 108 + 112 + 100 + 72 + 28 = 575. The cube of 8 is 512, so, as I expected, the deviation from the sequence of perfect cubes continues to widen. Here, also, is a picture for the next of these figures, when n = 8.
Now it is time for the analysis of differences in this sequence, the differences in those differences, and so on. Here goes….
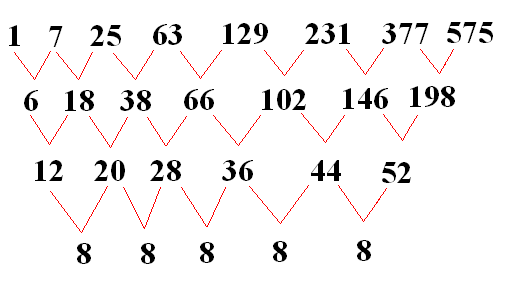Now this is helpful! It tells me that the solution to this problem will take the form a third-order polynomial, also known as a cubic equation — so my earlier idea that this sequence was not related to the perfect cubes was, I now know, completely false.
I next struggled, for several hours, to find the cubic equation for the solution to this problem, without success. After finally giving up on finding the solution myself, I asked my wife to assist me (she’s also a math teacher, and her knowledge of algebra exceeds my own, for I specialize in geometry). She performed a cubic regression, and this is how we now know that the solution to this problem is that the number of cells for the nth figure in this sequence equals (4/3)n3 – 2n2 + (8/3)n – 1. I spent many hours on this problem, but my wife finished solving it in mere minutes!
It’s no wonder I couldn’t find this solution, for I was only considering integers as coefficients, since only whole numbers for answers make sense — which I thought, incorrectly, would require the coefficients to be integers. However, for every value of n I have tested, the number of thirds in the answer always ends up being a multiple of three, cancelling threes in all denominators, and yielding whole numbers for answers. In retrospect, this makes sense, considering that the octahedron is a dipyramid, and that there is a 1/3 in the pyramid’s volume formula.
I was originally seeking to make an informative and interesting blog-post when I started this. However, I didn’t anticipate that I would learn as much as I did from the experience. I’m giving my wife joint credit for this solution, for I would not have been able to solve this problem without her help.
[Later edit: more information about this sequence can be found on these two websites: http://en.wikipedia.org/wiki/Centered_octahedral_number and https://oeis.org/A001845. I did not know about these sites until after I had finished this post.]
RobertLovesPi.net 