Yesterday, I played for the first time with GeoMag toys, which I recently purchased. I was quite surprised to have what I believe to be a near-miss to the Johnson solids appear before me, one I’ve never seen, within just a few minutes:
 Here’s what it looks like, when viewed from two other angles.
Here’s what it looks like, when viewed from two other angles.

SANYO DIGITAL CAMERA

SANYO DIGITAL CAMERA
The faces of this three-fold dihedral polyedron are six pentagons, twelve triangles, and nine quadrilaterals. The fact that it has been proven that only 92 Johnson solids exist means that all of these faces cannot be regular. However, the irregularity is so small that I could not detect it in this model.
Next, I used Polydrons to build a net of this near-miss candidate.

What to do next was obvious: remove the “belt” of nine quadrilaterals, creating a net for a second near-miss candidate.

Having constructed this net, I then returned GeoMags to build a 3-d model of this second, “unbelted” near-miss candidate.

SANYO DIGITAL CAMERA

SANYO DIGITAL CAMERA

SANYO DIGITAL CAMERA
I then wondered if I could make a third such solid by removal of the triangles, all of which appeared to be the lateral faces of pyramids.

SANYO DIGITAL CAMERA

SANYO DIGITAL CAMERA
Could I remove them? Yes, and I did so. Did this create a third near-miss candidate? No. The resulting polyhedron, shown immediately above, is non-convex, and therefore cannot be a near-miss. The faces with dihedral angles greater than 180° are the triangle-pairs found where the pyramids were in the previous model.
With the “belted” and “unbelted” polyhedra before this non-convex non-candidate, the next step is to share them with other polyhedra enthusiasts, get their input regarding the question of whether these are genuine near-misses, and see if these polyhedra have already been found, unknown to me, by someone else.
[Update: please see the next two posts for more on these near-miss candidates.]


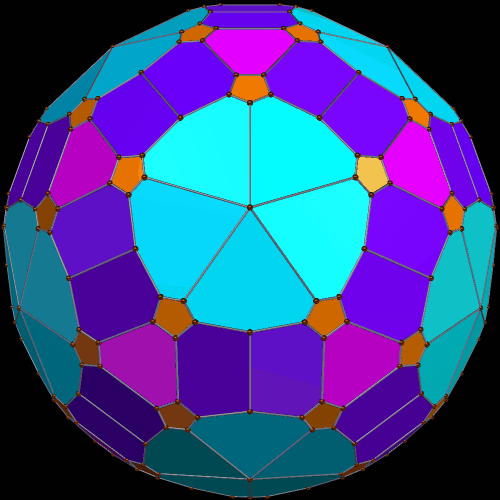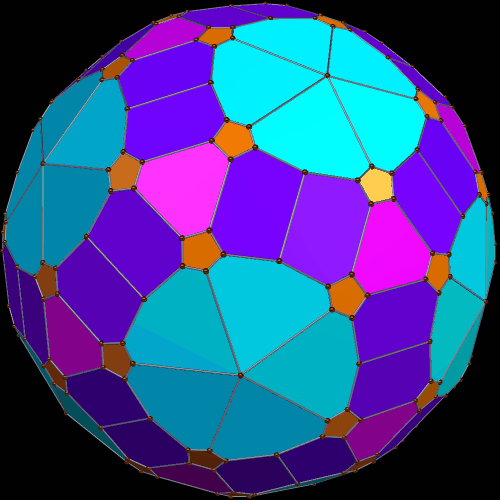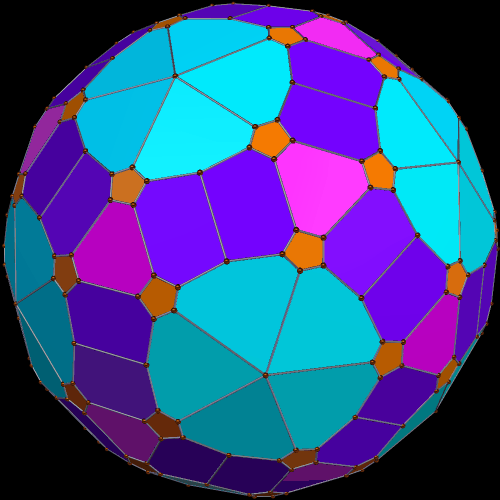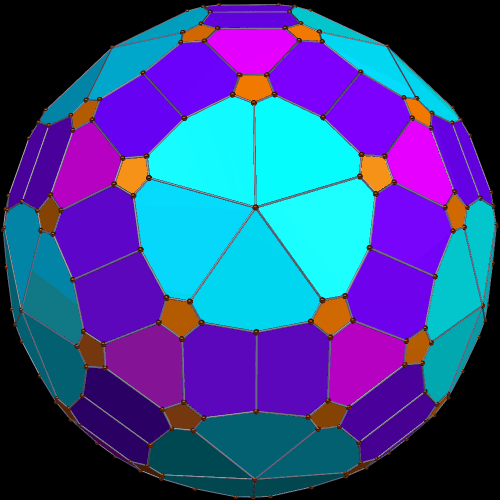








 Here’s what it looks like, when viewed from two other angles.
Here’s what it looks like, when viewed from two other angles.











































