About RobertLovesPi

I go by RobertLovesPi on-line, and am interested in many things, a large portion of which are geometrical. Welcome to my own little slice of the Internet. The viewpoints and opinions expressed on this website are my own. They should not be confused with those of my employer, nor any other organization, nor institution, of any kind.

Places I Have Been, #2: When Was I Last There?

Posted on 11 July 2015 by RobertLovesPi

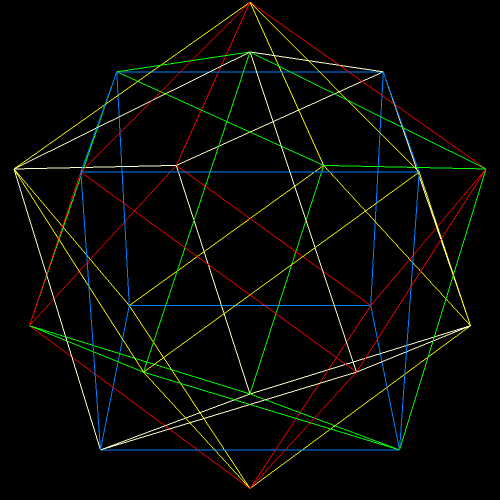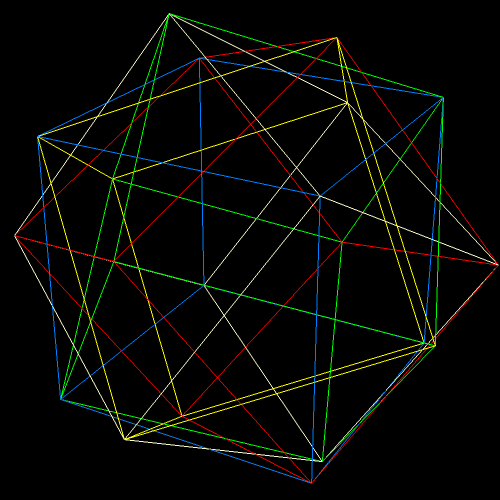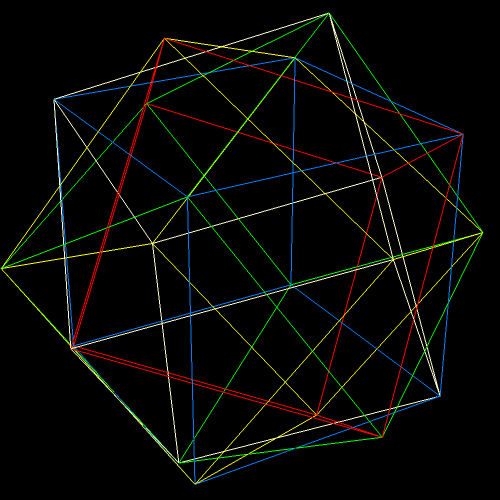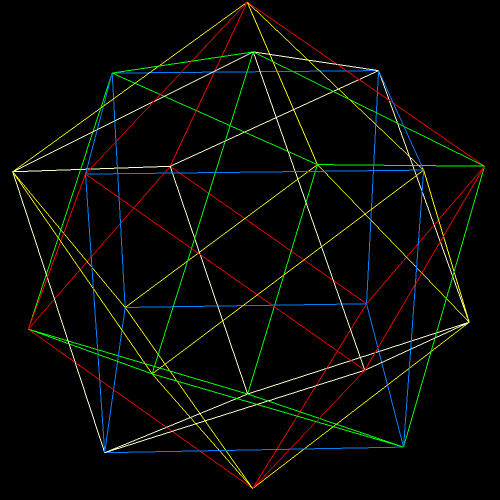
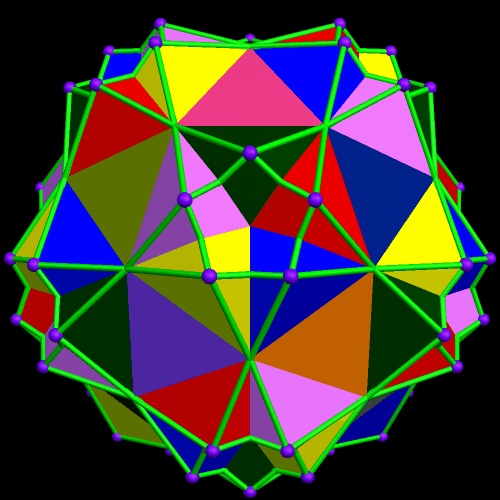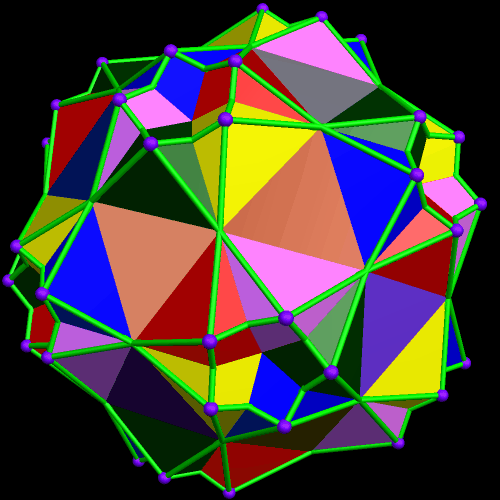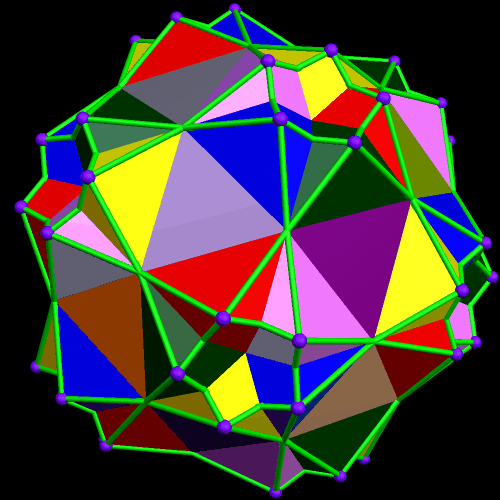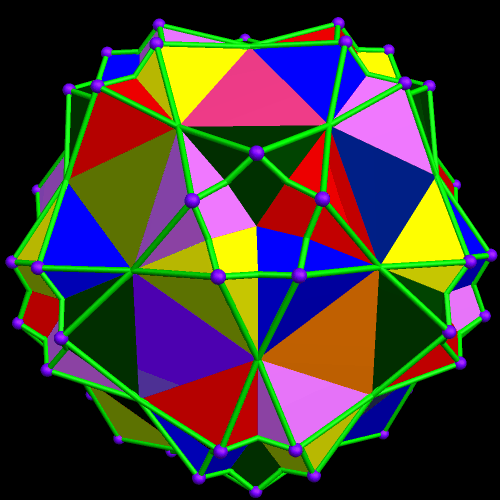
This is a more detailed version of one of the earliest posts on this blog, “Places I Have Been.” In this version, I color-coded the states and provinces to show when I was last in each of these places (the color-coding is explained below the picture). Also, no, I haven’t left North America — yet — but visits to all the other continents on Earth, plus the Moon, are definitely on my lifetime “to do” list.

Here’s the color-key. It starts in the present, and then proceeds in reverse chronological order.

Red — I’m here right now. Arkansas is also the state where I have spent well over 90% of my life, and I was born here, as well, 47½ years ago (January, 1968).

Pink — These are states I’ve been to since turning 45, not counting where I am at the moment. It’s also the set of states my wife and I have visited together — so far.

Purple — I was last in each of these states during the first half of my forties.

Dark blue — I was last in Kansas in my thirties, flying there, with two other math teachers, for an educational conference.

Yellow — Louisiana is the only state which I last visited in my twenties.

Green — These are states I last visited at age nineteen. So far, that’s the furthest I have traveled in a single year. The green Mexican state on the map is Chihuahua, where I visited Cuidad Juárez, just across the Rio Grande from El Paso, Texas.

Light blue — These are the states and provinces I last visited as a “tween” (ages 10-12). The Northern vacation trip was with my family, and, so far, that’s the only time I’ve been to Canada. Virginia made the map when I won a trip to Washington, DC (too small to be seen above), as one of a busload of young newspaper carriers, for selling twenty newspaper subscriptions to Arkansas Gazette — one of America’s many “lost newspapers,” and one which I very much miss. Alabama and Florida are included because of a field trip, all the way to Key West, with a college class — one of the benefits of growing up as a “professor’s kid” who spent a lot of time on campus.

Brown — I have been to South Carolina once, but I wasn’t even close to ten years old at the time, and now I barely remember this family trip to the Atlantic coast.

Gray — I was so young, when my parents took me to Colorado, that I have no memories from that trip at all. I don’t think my younger sister had even been born yet, in fact. All I remember is being told, much later, that, yes, I have been to Colorado.

Riddle: How did the chemist accidentally kill his dog?

Posted on 10 July 2015 by RobertLovesPi

Answer: He fed him a whole can of aluminum phosphate.

Disclaimers: (1) no actual dogs were harmed in the making of this awful pun, and (2) yes, I actually did the math regarding the toxicity of aluminum phosphate. Don’t feed it to your dog!

Trinary Rhombicosidodecahedra

Posted on 6 July 2015 by RobertLovesPi

This image of three rhombicosidodecahedra “orbiting” a common center was made with Stella 4d, a program you may try for free at this website.

Tidally Locked Binary Icosidodecahedra

Posted on 28 June 2015 by RobertLovesPi

I’ve been trying to figure out for over a year how to make images like the one above, without having holes in the two polyhedra, facing each other. At last, that puzzle of polyhedral manipulation using Stella 4d (software available at this website) has been solved: use augmentation followed by faceting, rather than augmentation followed by simply hiding faces.

Two Similar Polyhedra with Icosidodecahedral Symmetry

Posted on 28 June 2015 by RobertLovesPi

Both of these were made using Stella 4d, software you can try at this website.

Three Different Depictions of the Compound of Five Cubes

Posted on 28 June 2015 by RobertLovesPi

The most common depiction of the compound of five cubes uses solid cubes, each of a different color:

This isn’t the only way to display this compound, though. If the faces of the cubes are hidden, then the interior structure of the compound can be seen. An edges-only depiction, still keeping a separate color for each cube, looks like this:

If these thin edges are then thickened into cylinders, that makes a third way to depict this polyhedral compound. It creates a minor problem, though: edges-as-cylinders looks awful without vertices shown as well, and the best way I have found to depict vertices, in this situation, is with spheres. With vertices shown as spheres, however, a sixth color, only for the vertex-spheres, is needed. Why? Because each vertex is shared by six edges: three from a cube of one color, and three from a second cube, of a different color.

Finally, here are all three versions, side-by-side for comparison, and with the motion stopped.

All images in this post were created using Stella 4d: Polyhedron Navigator, software you may try for free at this website.

My New Middle Initial and Name: A Mathematical Welcome-Back Gift from My Alma Mater

Posted on 27 June 2015 by RobertLovesPi

I just had a middle initial assigned to me, and then later, with help, figured out what that initial stood for. With apologies for the length of this rambling story, here’s an explanation for how such crazy things happened.

I graduated from high school in 1985, and then graduated college, for the first time, with a B.A. (in history, of all things), in 1992. My alma mater is the University of Arkansas at Little Rock, or UALR, whose website at http://www.ualr.edu is the source for the logo at the center of the image above.

Later, I transferred to another university, became certified to teach several subjects other than history, got my first master’s degree from there (also in history) in 1996, and then quit seeking degrees, but still added certification areas and collected salary-boosting graduate hours, until 2005. In 2005, the last time I took a college class (also at UALR), I suddenly realized, in horror, that I’d been going to college, off and on, for twenty years. That, I immediately decided, was enough, and so I stopped — and stayed stopped, for the past ten years.

Now it’s 2015, and I’ve changed my mind about attending college — again. I’ve been admitted to a new graduate program, back at UALR, to seek a second master’s degree — one in a major (gifted and talented education) more appropriate for my career, teaching (primarily) mathematics, and the “hard” sciences, for the past twenty years. After a ten-year break from taking classes, I’ll be enrolled again in August.

As part of the process to get ready for this, UALR assigned an e-mail address to me, which they do, automatically, using an algorithm which uses a person’s first and middle initial, as well as the person’s legal last name. With me, this posed a problem, because I don’t have a middle name.

UALR has a solution for this: they assigned a middle initial to me, as part of my new e-mail address: “X.” Since I was not consulted about this, I didn’t have a clue what the “X” even stands for, and mentioned this fact on Facebook, where several of my friends suggested various new middle names I could use.

With thanks, also, to my friend John, who suggested it, I’m going with “Variable” for my new middle name — the name which is represented by the “X” in my new, full name.

I’ve even made this new middle initial part of my name, as displayed on Facebook. If that, plus the e-mail address I now have at UALR, plus this blog-post, don’t make this official, well, what possibly could?

Various Views of Three Different Polyhedral Compounds: Those of (1) Five Cuboctahedra, (2) Five of Its Dual, the Rhombic Dodecahedron, and (3) Ten Components — Five Each, of Both Polyhedra.

Posted on 26 June 2015 by RobertLovesPi

Polyhedral compounds differ in the amount of effort needed to understand their internal structure, as well as the way the compounds’ components are assembled, relative to each other. This compound, the compound of five cuboctahedra, and those related to it, offer challenges not offered by all polyhedral compounds, especially those which are well-known.

The image above (made with Stella 4d, as are others in this post — software available here) is colored in the traditional style for compounds: each of the five cuboctahedra is assigned a color of its own. There’s a problem with this, however, and it is related to the triangular faces, due to the fact that these faces appear in coplanar pairs, each from a different component of the compound.

The yellow regions above are from a triangular face of the yellow component, while the blue regions are from a blue triangular face. The equilateral triangle in the center, being part of both the yellow and blue components, must be assigned a “compromise color” — in this case, green. The necessity of such compromise-colors can make understanding the compound by examination of an image more difficult than it with with, say, the compound of five cubes (not shown, but you can see it here, if you wish). Therefore, I decided to look at this another way: coloring each face of the five-cuboctahedra compound by face type, instead of by component.

Another helpful view may be created by simply hiding all the faces, revealing internal structure which was previously obscured.

Since the dual of the cuboctahedron is the rhombic dodecahedron, the dual of the compound above is the compound of five rhombic dodecahedra, shown, first, colored by giving each component a different color.

A problem with this view is that most of what’s “going on” (in the way the compound is assembled) cannot be seen — it’s hidden inside the figure. An option which helped above (with the five-cuboctahedra compound), coloring by face type, is not nearly as helpful here:

Why wasn’t it helpful? Simple: all sixty faces are of the same type. It can be made more attractive by putting Stella 4d into “rainbow color” mode, but I cannot claim that helps with comprehension of the compound.

With this compound, what’s really needed is a “ball-and-stick” model, with the faces hidden to reveal the compound’s inner structure.

Since the two five-part compounds above are duals, they can also be combined to form a ten-part compound: that of five cuboctahedra and five rhombic dodecahedra. In the first image below, each of the ten components is assigned its own color.

In this ten-part compound, the coloring-problem caused in the first image in this post, coplanar and overlapping triangles of different colors, vanishes, for those regions of overlap are hidden in the ten-part compound’s interior. This is one reason why this coloring-scheme is the one I find the most helpful, for this ten-part compound (unlike the two five-part compounds above). However, so that readers may make this choice for themselves, two other versions are shown below, starting with coloring by face type.

Finally, the hollow version of this ten-part compound. This is only a personal opinion, but I do not find this image quite as helpful as was the case with the five-part compounds described above.

Which of these images do you find most illuminating? As always, comments are welcome.

99% of Critical

Posted on 23 June 2015 by RobertLovesPi

Created using Stella 4d: Polyhedron Navigator, software which is available for either purchase, or a free trial download, right here.

Flying Kites into the Snub Dodecahedron, a Dozen at a Time, Using Tetrahedral Stellation

Posted on 12 June 2015 by RobertLovesPi

I’ve been shown, by the program’s creator, a function of Stella 4d which was previously unknown to me, and I’ve been having fun playing around with it. It works like this: you start with a polyhedron with, say, icosidodecahedral symmetry, set the program to view it as a figure with only tetrahedral symmetry (that’s the part which is new to me), and then stellate the polyhedron repeatedly. (Note: you can try a free trial download of this program here.) Several recent posts here have featured polyhedra created using this method. For this one, I started with the snub dodecahedron, one of two Archimedean solids which is chiral.

Using typical stellation (as opposed to this new variety), stellating the snub dodecahedron once turns all of the yellow triangles in the figure above into kites, covering each of the red triangles in the process. With “tetrahedral stellation,” though, this can be done in stages, producing a greater variety of snub-dodecahedron variants which feature kites. As it turns out, the kites appear twelve at a time, in four sets of three, with positions corresponding to the vertices (or the faces) of a tetrahedron. Here’s the first one, featuring one dozen kites.

Having done this once (and also changing the colors, just for fun), I did it again, resulting in a snub-dodecahedron-variant featuring two dozen kites. At this level, the positions of the kite-triads correspond to those of the vertices of a cube.

You probably know what’s coming next: adding another dozen kites, for a total of 36, in twelve sets of three kites each. At this point, it is the remaining, non-stellated four-triangle panels, not the kite triads, which have positions corresponding to those of the vertices of a cube (or the faces of an octahedron, if you prefer).

Incoming next: another dozen kites, for a total of 48 kites, or 16 kite-triads. The four remaining non-stellated panels of four triangles each are now arranged tetrahedrally, just as the kite-triads were, when the first dozen kites were added.

With one more iteration of this process, no triangles remain, for all have been replaced by kites — sixty (five dozen) in all. This is also the first “normal” stellation of the snub dodecahedron, as mentioned near the beginning of this post.