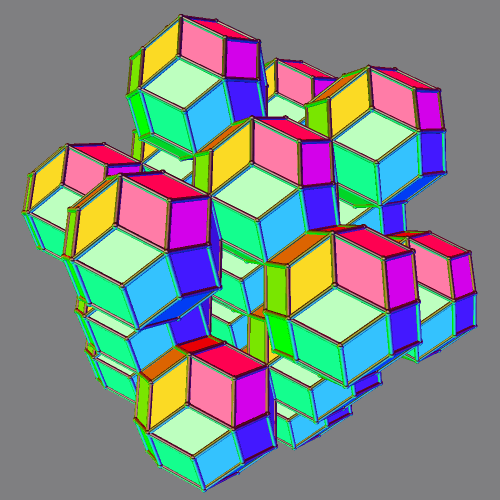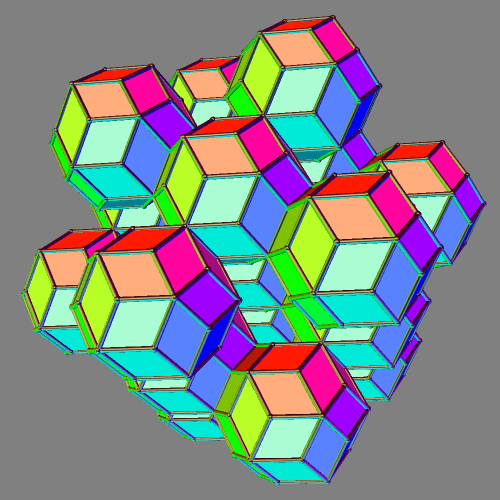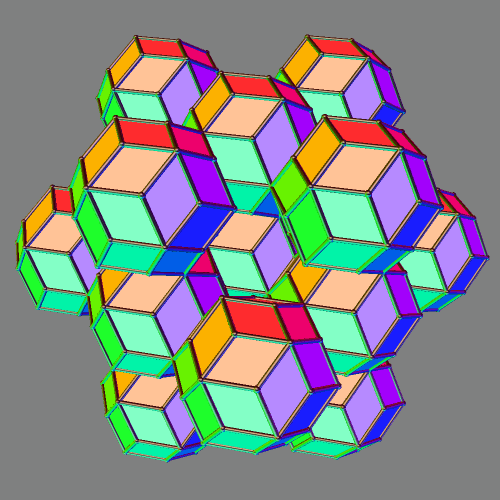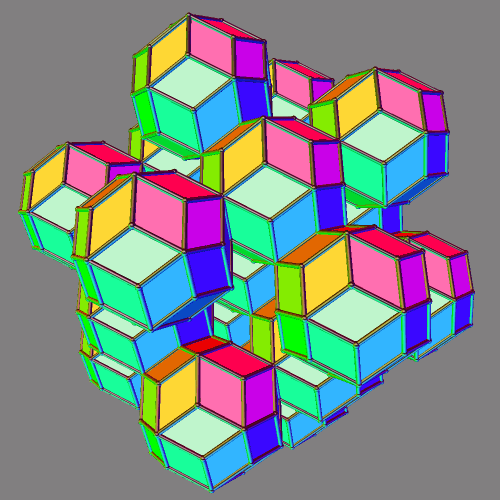I just returned home from a visit to my local library, and was so bewildered by this sign at the entrance that I felt compelled to take a picture of it. Helium doesn’t react with anything at all . . . so why would a library want to ban helium balloons? It’s not like helium can damage books!
Author Archives: RobertLovesPi
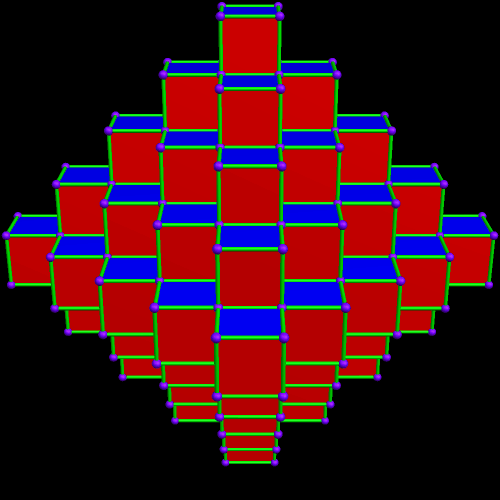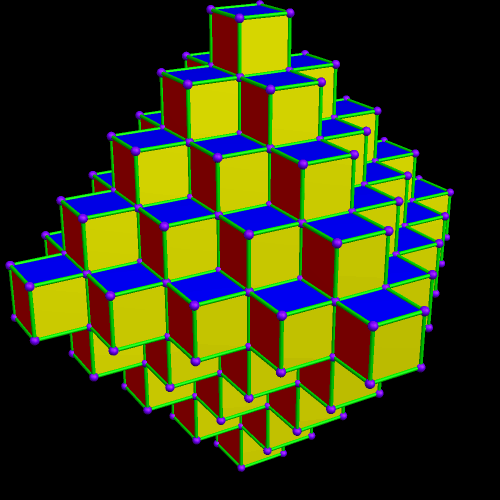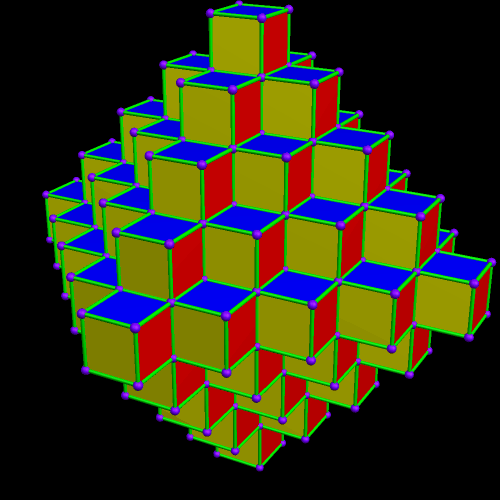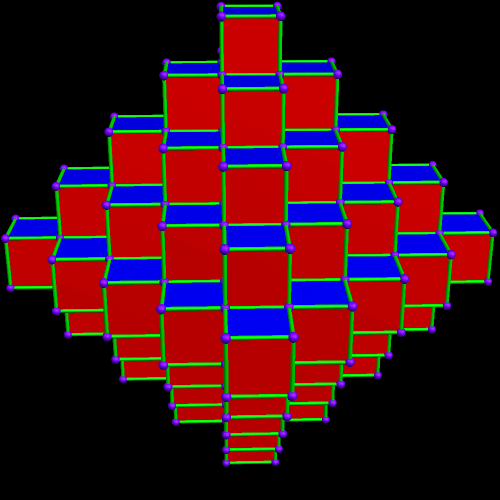
An Octahedron Made of Cubes
Software credit: I made this using Stella 4d, which is available at http://www.software3d.com/Stella.php.
My Aqua Regia Story
This is my twentieth year teaching, but only the first year when I have not taught at least one class in chemistry, and I miss it. One of my fondest memories of chemistry lab involves the one time I experimented with aqua regia — a mixture of acids which, unlike any single acid, can dissolve both gold and platinum, the “noble metals.” I had read a story of a scientist’s gold Nobel Prize being protected from the Nazis by dissolving it in aqua regia, and then recovering the gold from solution after World War II had ended. Having read about this, I wanted to try it myself, and also thought it would make an excellent lab for classroom use — if I could figure out how to recover the gold, and also learn what precautions would be needed to allow high school students to perform this experiment safely. For sensible and obvious reasons, I conducted a “trial run” without students present, but with another chemistry teacher nearby, since aqua regia, and the gases it produces when dissolving gold, are quite dangerous. Someone else has put a video on YouTube, showing aqua regia dissolving gold, so you can see something much like what I saw, simply by watching this video.
First, I obtained one-tenth of a troy ounce of gold, which cost about $80 at the time. I had read about the extreme malleability of gold, one of the softest metals, and wanted to see evidence for it for myself — so, before I prepared the the aqua regia, I used a hammer to try flattening the gold sample into a thin sheet. That didn’t work, but it didn’t take long for me to figure out why — I had accidentally bought gold coin-alloy, which is 10% copper, not pure gold. Since this alloy is far less malleable than pure gold, my attempt to flatten it had failed, but I also knew this would not pose a problem for my primary experiment — the one involving aqua regia. Also, I didn’t have another spare $80 handy, to purchase another 1/10 troy ounce of pure gold, so I proceeded to make, for the first time in my life, a small amount of aqua regia — Latin for “royal water.”
Unlike what is shown in the video above, I prepared the acid-mixture first, before adding the gold, using a slightly-different recipe: the traditional 1:4 ratio, by volume, of concentrated nitric acid to concentrated hydrochloric acid. Both these acids look (superficially) like water, but the mixture instantly turned yellow, and started fuming, even before anything was added to it. Wearing full protective gear, I watched it for a few minutes — and then, using tongs held by gloved hands, lowered my hammer-bashed sample of gold into the fuming, yellow mixture of concentrated acids.
It worked. It was a fascinating reaction, and a lot of fun to watch. At approximately the same time that the last of my gold sample dissolved, something occurred to me: I had failed to research how to recover the dissolved gold from the resulting solution! No problem, I thought — I can figure this out. (I am seldom accused of lacking self-confidence, even when I’m wrong.)
My first idea was to use a single-replacement reaction. Many times, I have had students extract pure silver from a solution of silver nitrate by adding a more-active metal, such as copper. The copper dissolves, replacing the silver in the silver nitrate solution, and silver powder forms, as a precipitate, on the surface of the copper. Thinking that a similar process could be used to precipitate out the gold from my gold / aqua regia mixure, I simply added come copper to the reaction beaker. The corrosive properties of my aqua regia sample had not yet been exhausted, though, and so the remaining aqua regia simply “ate” the copper. The result was a mess — I had only succeeded in turning an already-complicated problem into an even-more-complicated problem, by adding more chemicals to the mixture. More attempts to turn the gold ions back into solid gold dust, using other chemicals, followed, but all of them failed. Finally, I used a strong base, sodium hydroxide, to neutralize the still-acidic mixture, and then, disgusted by my failure to recover the gold, found a way to safely dispose of the mixture, and did so.
In retrospect, I think I know where I messed up — I should have neutralized the remaining acids in the mixture with sodium hydroxide first, before adding copper to cause the gold to precipitate out, in a no-longer-acidic solution of ions with much less hydronium present. That, I think, will work, and I do intend to try it sometime — after doing more research first, to increase my level of certainty, and also after waiting for the current price of gold to drop to less-expensive levels. Right now, after all, a tenth of a troy ounce of gold costs roughly $120, not a mere $80.
As for the lost $80, I’m not upset about that anymore. I definitely learned things while doing this, and now view the $80 spent as simply the cost of tuition for an educational experience.
At Least for Me, Blogging > Writing a Book
I’ve been asked, more than once, if I’ve ever considered writing a book. The answer: writing a book, as compared to maintaining a blog, would drive me crazy. The reason is simple: every book I’ve every read has at least one typo in it — somewhere. If I wrote a book, got it published, and then found writing mistakes in it, I’d be mortified. With a blog, on the other hand, I can edit mistakes away, months, or even years, after making them.
There aren’t many things that embarrass me, but making errors in writing is definitely one of them. If others can see the errors, then having committed the “sin” of writing incorrectly feels like being caught naked in public — eeeeek!
Recovering from Theophobia: My Personal, Secular Jihad
The image above is a 19th-Century painting by Eugène Delacroix, depicting the story of Jacob, wrestling with a being often described as an angel, as described in the Book of Genesis. An interesting part of the story is that there were no witnesses to this struggle in the darkness (“So Jacob was left alone, and a man wrestled with him till daybreak,” Gen. 32:24, NIV), which tells me that the conflict could have occurred entirely inside Jacob’s mind. It does not matter if there was, or was not, an actual person, named Jacob, who had such an experience. No supernatural beliefs are necessary to find this story interesting, and there is no good reason to avoid thinking about it.
Thought is, of course, a mental activity which can bring clarity to confusing things in life, just as a sunrise can enable one to see things which have previously been hidden by night. There are times when thinking requires solitude, and the process of figuring out difficult problems usually doesn’t succeed without some sort of internal struggle. If you have ever wrestled with a single, difficult mathematical problem for several days running, as I have, then you understand this already — but the need for clear, rational thinking is certainly not limited to the field of mathematics. Rational thought is important in all parts of life.
Whether we like it or not, life contains a series of both external and internal struggles. Many people dislike conflict, and go to great lengths to avoid it. I am not one of those people, but this is not by choice. It is, rather, a result of the fact that I was born into an intense struggle-in-progress: the efforts of my now-deceased father, a religious fanatic, to control the lives of everyone around him, and use them for his own selfish purposes — and the efforts of some of these other people, myself included, to escape his efforts to control every facet of our lives. From an early age, out of necessity, I had to develop complex techniques of mental and verbal combat, both defensive and offensive, simply to survive childhood with some semblance of sanity intact — although the resulting PTSD, from growing up in the war zone I called “home,” is something with which I will always have to cope. My earliest memory, after all, is surviving shaken baby syndrome at age 2½, and that sort of experience simply cannot be escaped without consequences.
My mental-combat techniques still exist, available for use at any time of my choosing, and can have devastating impact on others — I seldom lose an argument — but using these verbal and mental weapons at full power is, I now realize, quite dangerous, more so to myself than to anyone else. Now, decades later, I still have to be careful not to be overly eager to jump headlong, as if by instinct, into any conflict which presents itself, especially if I see those I care about being bullied, or otherwise abused. I have neither the time, nor the mental energy, to fight every single injustice I see, but it took many years for me to understand the wisdom of the well-known saying that it is important to choose one’s battles carefully.
The word “jihad,” which I deliberately used in the title of this post, is complex, and has multiple definitions. It is also an emotionally-charged word, and out-of-control emotions are, perhaps, the greatest enemy of rational thought. So, first, please understand this: when I use this word, I am not referring to any sort of “holy war,” which is the first thing that comes to mind, for many people, when they hear what I sometimes call the “j-word.” I am also not making any sort of comment for, nor against, Islam, but am simply borrowing a word from another language, Arabic, because it applies so well to much of my own life. Another definition you will find here is “a personal struggle in devotion to Islam especially involving spiritual discipline” — in other words, an internal struggle to do the right thing. While I am not religious in any conventional sense, I definitely understand the important idea of an internal, mental — or “spiritual,” if you prefer — struggle. My personal internal struggle involves a never-ending effort to maintain self-control, especially over destructive emotions, such as hatred, and fury. Fury isn’t simply anger, after all — it goes far beyond that. It is an absolutely horrific state of mind where one is so overcome by anger that the rational self becomes utterly consumed by white-hot, blinding rage.
For years, without realizing it, I was a theophobe — hardly surprising, considering the religious elements of the more unpleasant parts of my childhood. Theophobia is not a familiar word to most people, but it can exist in both religious and non-religious people, and can be defined as an irrational fear and hatred of God, religion, religious people, and religious institutions, such as churches and mosques. There have been entire years — especially since the Catholic Church’s pedophilia scandal blew wide-open in the media, worldwide — when I could not bring myself to go near a church of any denomination, let alone enter one, for fear that being near such a place would trigger a panic attack, or, even worse, a PTSD “freakout” episode. It isn’t hard to spot theophobes, of course; they are easily identified, especially among the much larger, rapidly-growing group of people who call themselves atheists. You probably know at least a few atheists yourself, and might have noticed that some of them seem to be at peace with life, and can easily interact peacefully with religious people — while others are a perfect fit for the “angry atheist” stereotype, attacking religion as if it were the source of all evil in the world. It isn’t, but that didn’t stop me from thinking that it was, for many years. Recovering from theophobia is not easy, and is definitely a struggle, but is also very much worth the effort.
Unusually, several of the people I am now grateful to, specifically for helping me recover from theophobia, are practicing Muslims. This doesn’t fit the stereotype of Islam portrayed in the Western media, of course. If you get all of your information about Islam from stories in the news, you might think all Muslims hijack airplanes, commit suicide bombings, oppress women, and decapitate “infidels” every time they get they chance. Fortunately, I started using another approach, while still in college: conversation. Simply by talking to Muslims I am now proud to call my friends, I have learned several things, among them that most Muslims are kind and decent people, and also that most Muslims intensely dislike the extremists within Islam — about as much as the average Christian dislikes, say, the Westboro Baptist Church. Adding practicing Christians to the list of people I can successfully engage in productive conversation took a lot longer, but the reason for this has absolutely nothing to do with Christianity, and everything to do with my own personal history. My father was, after all (among many other things), an ordained Christian minister. Later, he moved through several other religions, attempting to drag my family along with him, and these religions included his own warped version of amalgamated Native American religious traditions, the Soka Gakkai sect of Buddhism, and several others. A notable absence on this list — one of the few religions with which my father never developed an obsession — is Islam. This fact made Islam, and those who practice it, a logical place for me to start the process of making peace with certain inescapable facts: (1) the world contains billions of religious people, most of whom are not dangerous fanatics, and (2) religion is not going away any time soon, no matter how much the furious theophobes of the world rage against it.
This personal recovery-process is not over; I still have much internal, mental work left to do, especially when it comes to establishing peace with Christianity, the world’s largest religion. The important thing, at this point, is that I am doing it. I’m quite happy to have left the “angry atheist” phase of my life in the past, where it belongs, and have no intention of returning there.
What Is a Mathematician?
A Polyhedral Journey, Beginning with Face-Based Zonohedrification of an Icosahedron
To begin this, I took an icosahedron, and made a zonish polyhedron with it, with the new faces based on the zones of the existing faces. Here’s the result.
Next, I started stellating the polyhedron above. At the sixth stellation, I found this. It’s a true zonohedron, and the first polyhedron shown here is merely “zonish,” because one has triangles, and the other does not. (One of the requirements for a polyhedron to be a zonohedron is that all its faces must have an even number of sides.)
 After that, I kept stellating, finding this as the 18th stellation of the first polyhedron shown here.
After that, I kept stellating, finding this as the 18th stellation of the first polyhedron shown here.
With this polyhedron, I then made its convex hull.
 At this point, the irregular hexagons were bothering me, so I used Stella 4d‘s “try to make faces regular” option. (Stella 4d is polyhedron-manipulation software you can try for free, or purchase, right here.)
At this point, the irregular hexagons were bothering me, so I used Stella 4d‘s “try to make faces regular” option. (Stella 4d is polyhedron-manipulation software you can try for free, or purchase, right here.)
The next step I chose was to augment all the yellow trapezoids with prisms, each with a height 1.6 times the trapezoids average edge length.
The next step was, again, to make the convex hull.
At this point, I tried “try to make faces regular” again, and was pleased with the result. The green rectangles became so thin, however, that I had to stop displaying the edges and vertices, in order for then to be seen.
 Next, I augmented both the blue faces (decagons) and the yellow faces (dodecagons) with antiprisms, again using a height 1.6 times that of the augmented faces’ average edge-lengths.
Next, I augmented both the blue faces (decagons) and the yellow faces (dodecagons) with antiprisms, again using a height 1.6 times that of the augmented faces’ average edge-lengths.
Next, I made the convex hull again — a step I often take immediately after augmenting a polyhedron.
This one surprised me, as it is more complicated than I expected. To clean things up a bit, I augmented only the trapezoids (dark pink) with prisms, and dodecagons (green) with antiprisms, again using the factor 1.6 for the augmentation-height.
The next step I chose was to take the convex hull, once more. I had not yet noticed that the greater height of the trapezoidal prisms would cause the dodecagonal antiprisms to be “lost” by this step, though.
Next, “try to make faces regular” was used again.
This last result had me feeling my polyhedral journey was going in circles, so I tried augmentation again, but in a different way. I augmented this polyhedron, using prisms, on only the red trapezoids (height factor, 1.6 again) and the blue rectangles (new height factor, 2.3 times average edge length).
After that, it was time to make another convex hull — and that showed me that I had, indeed, taken a new path.
 I found the most interesting faces of this polyhedron to be the long, isosceles trapezoids, so I augmented them with prisms, ignoring the other faces, using the new height-factor of 2.3 times average edge length this time.
I found the most interesting faces of this polyhedron to be the long, isosceles trapezoids, so I augmented them with prisms, ignoring the other faces, using the new height-factor of 2.3 times average edge length this time.
Of course, I wanted to see the convex hull of this. Who wouldn’t?
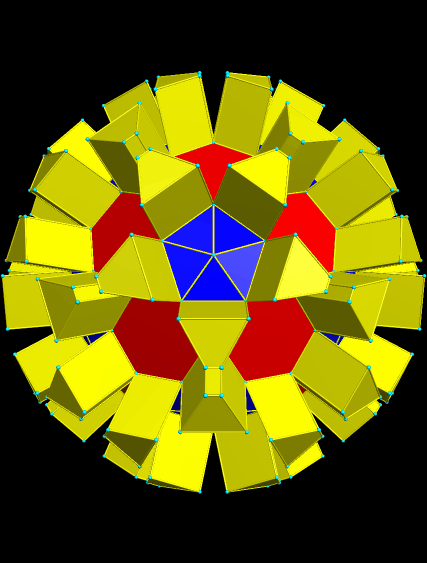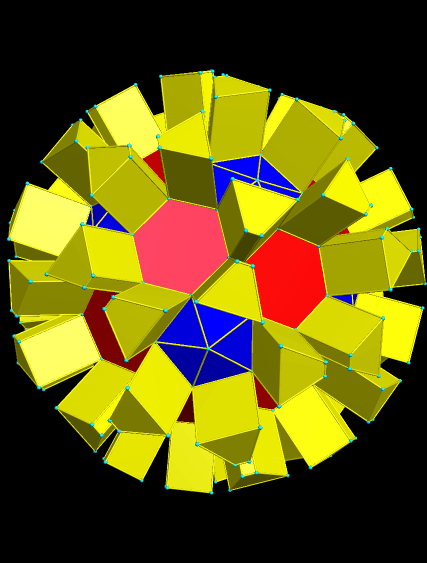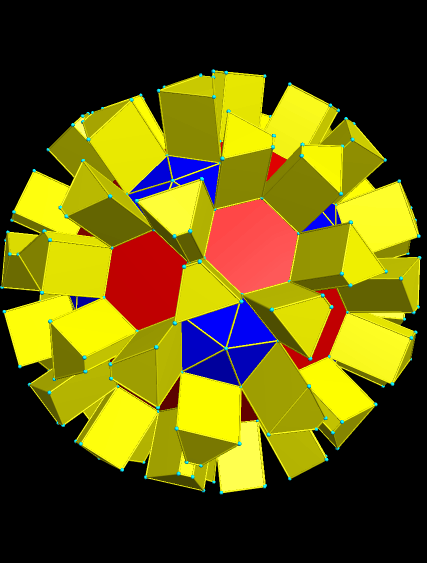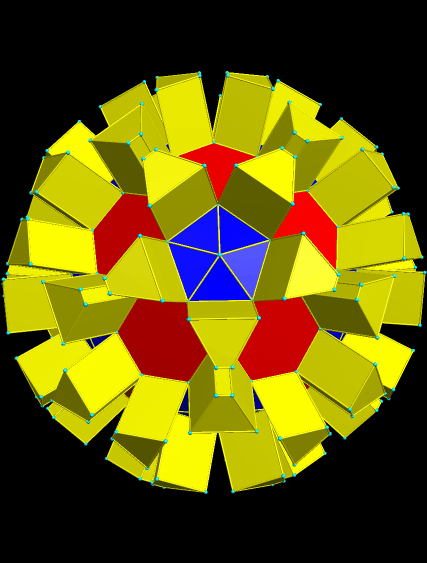
I then started to stellate this figure, choosing the 14th stellation as a good place to stop, and making the edges and vertices visible once more.
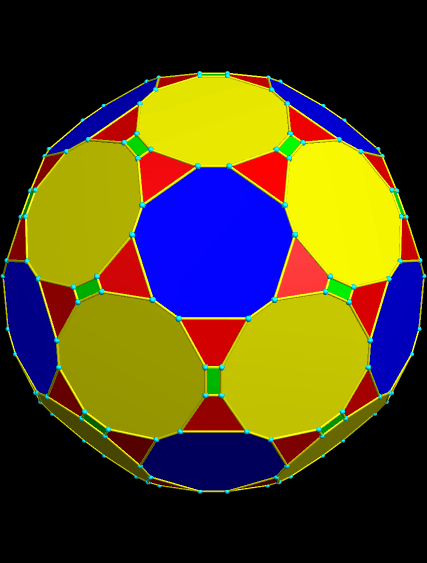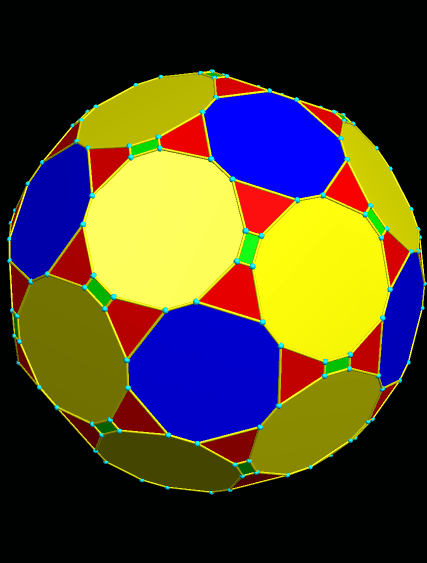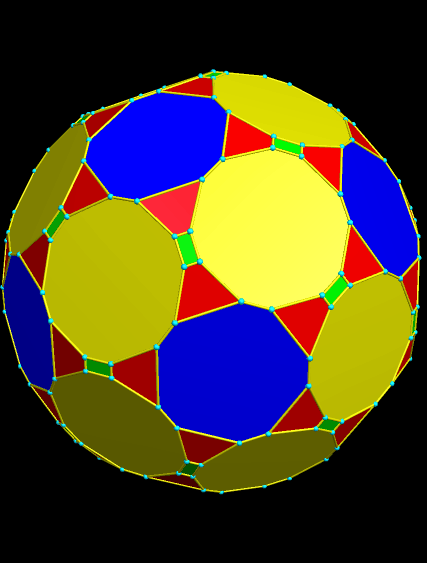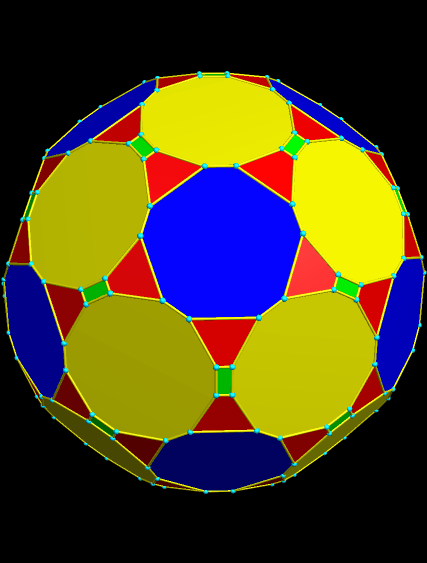
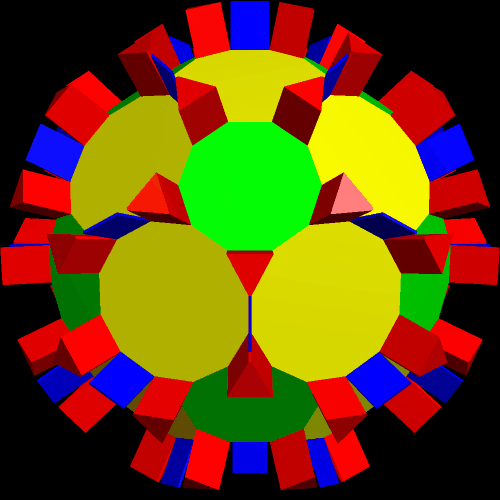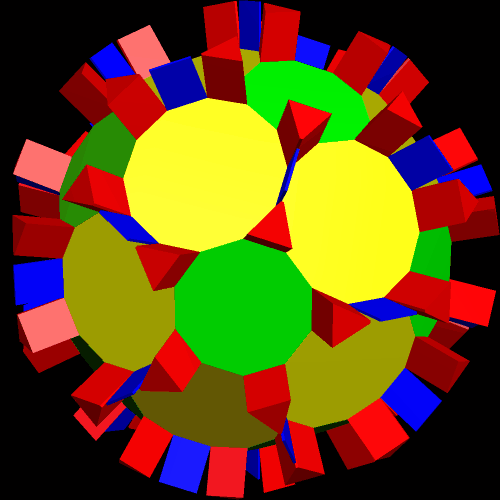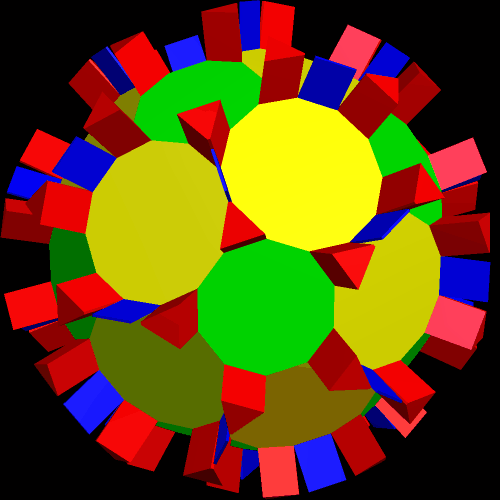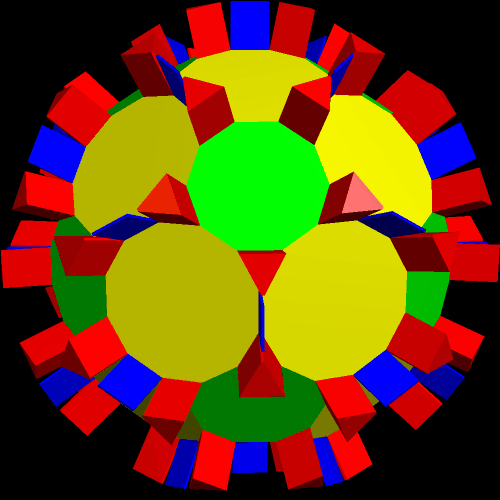
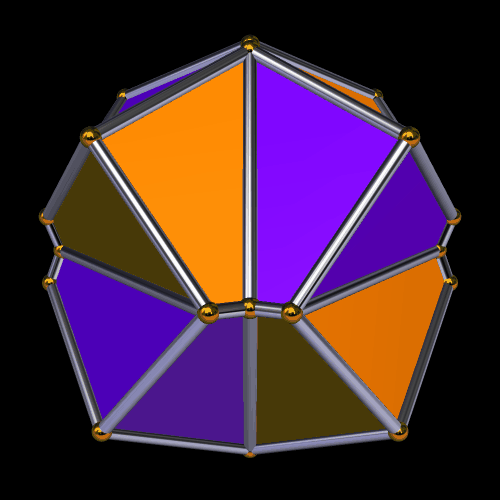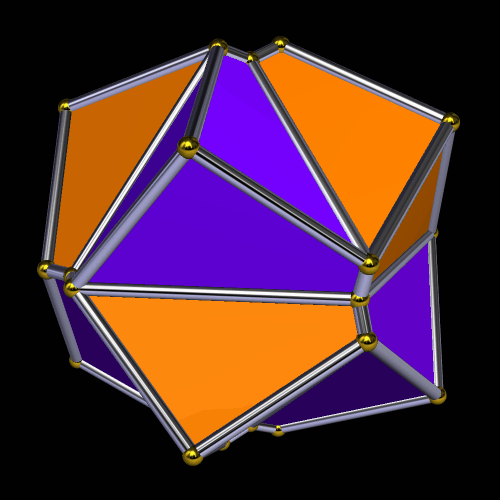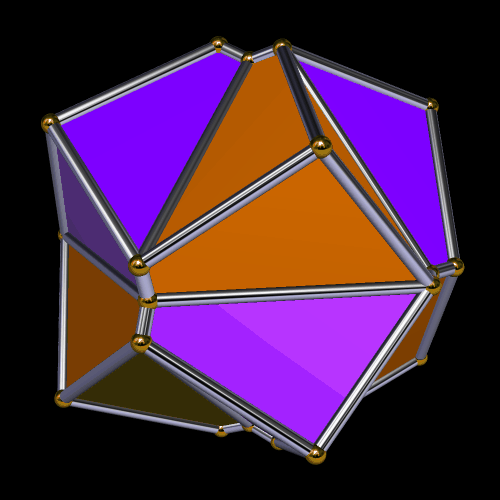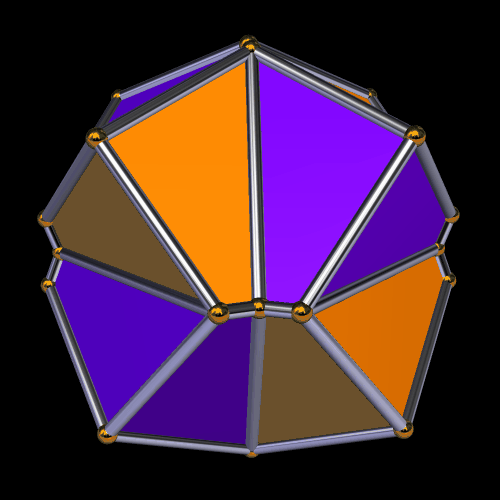
A Zonish Icosahedron, and Some of Its “Relatives”
To begin this, I used Stella 4d (available here) to create a zonish polyhedron from the icosahedron, by adding zones along the x-, y-, and z-axes. The result has less symmetry than the original, but it is symmetry of a type I find particularly interesting.
After making that figure, I began stellating it, and found a number of interesting polyhedra in this polyhedron’s stellation-series. This is the second such stellation:
This is the 18th stellation:
The next one, the 20th stellation, is simply a distorted version of the Platonic dodecahedron.
This one is the 22nd stellation:
This is the 30th stellation:
The next really interesting stellation I found was the 69th:
At this point, I returned to the original polyhedron at the top of this post, and examined its dual. It has 24 faces, all of which are quadrilaterals.
This is the third stellation of this dual — and another distorted Platonic dodecahedron.
This is the dual’s 7th stellation:
And this one is the dual’s 18th stellation:
At this point, I took the convex hull of this 18th stellation of the original polyhedron’s dual, and here’s what appeared:
Here is this convex hull’s dual:
Stella 4d, the program I use to make these (available here), has a built-in “try to make faces regular” function. When possible, it works quite well, but making the faces of a polyhedron regular, or even close to regular, is not always possible. I tried it on the polyhedron immediately above, and obtained this interesting result:
While interesting, this also struck me as a dead end, so I returned to the red-and-yellow convex hull which is the third image above, from right here, and started stellating it. At the 19th stellation of this convex hull, I found this:
I also found an interesting polyhedron as the 19th stellation of the dual which is three images above:
Cuboctahedral Cluster of Rhombic Triacontahedra
Due to their high number of planes of symmetry, rhombic triacontahedra make excellent building blocks to build other polyhedra. To make this, I used a program called Stella 4d, which you can try right here.