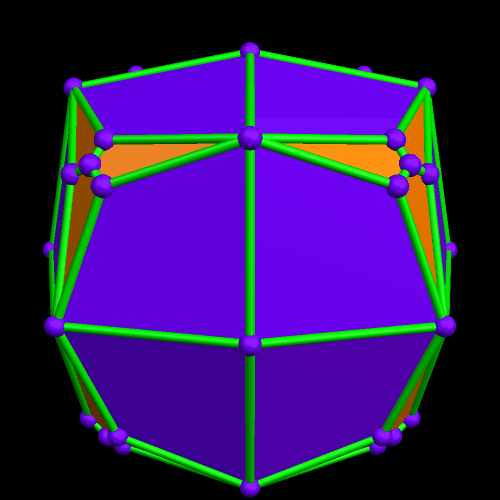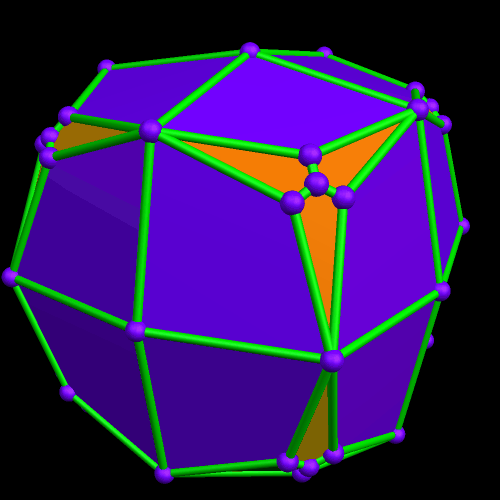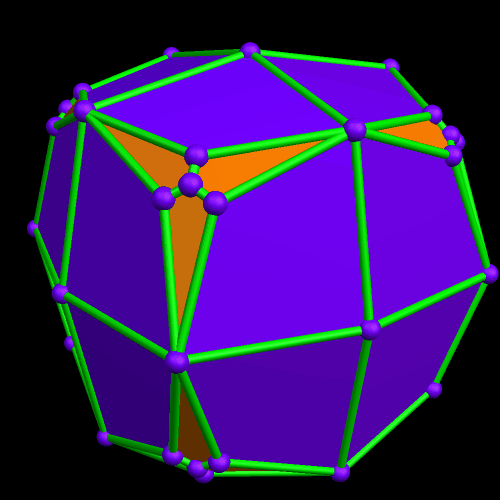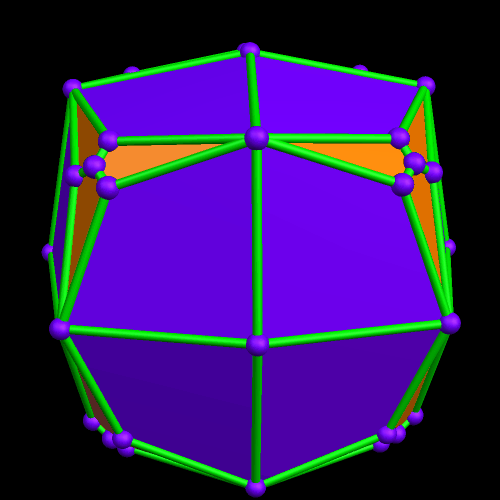
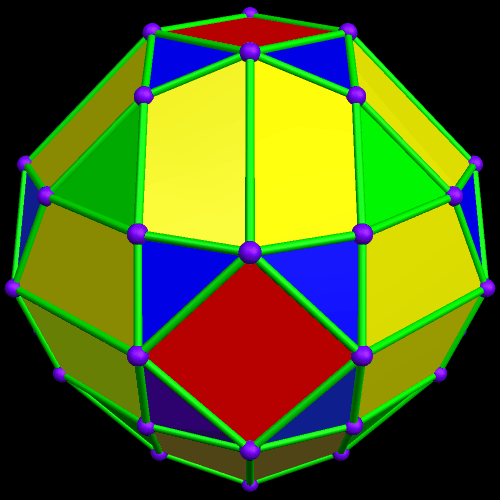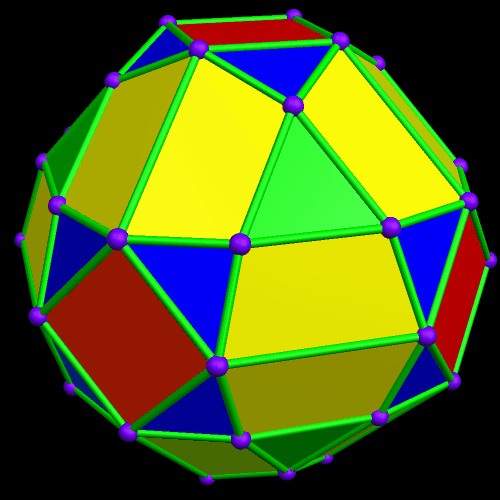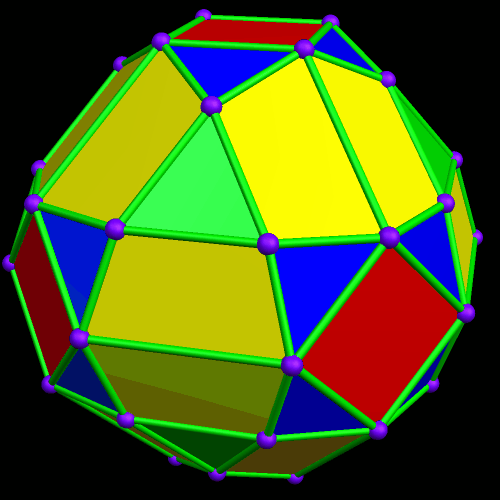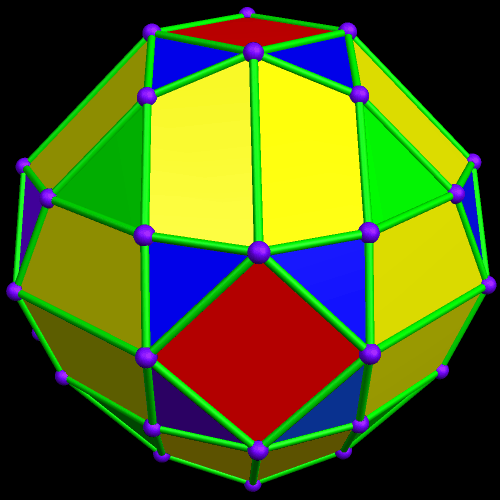
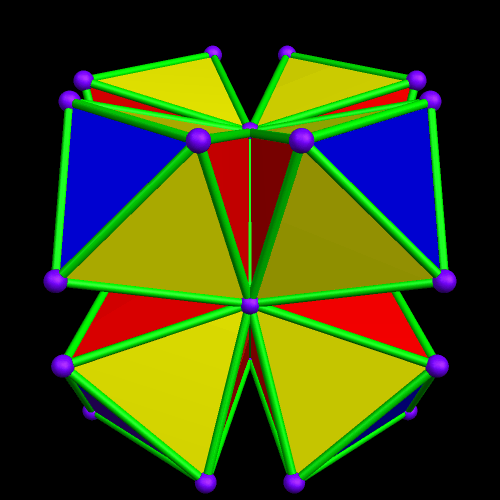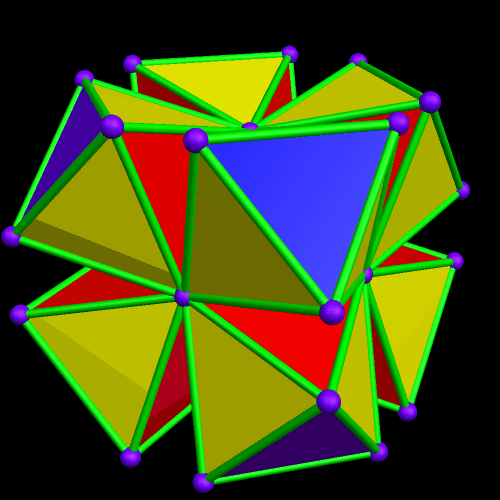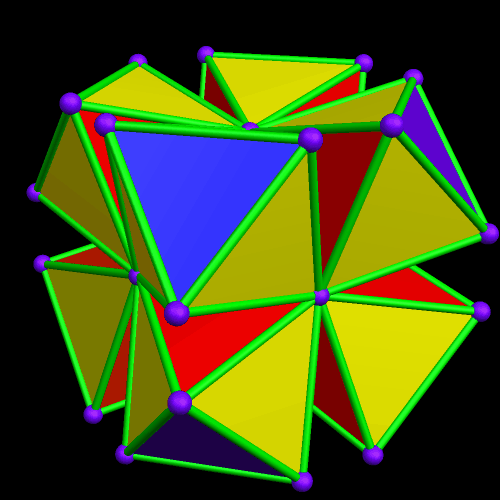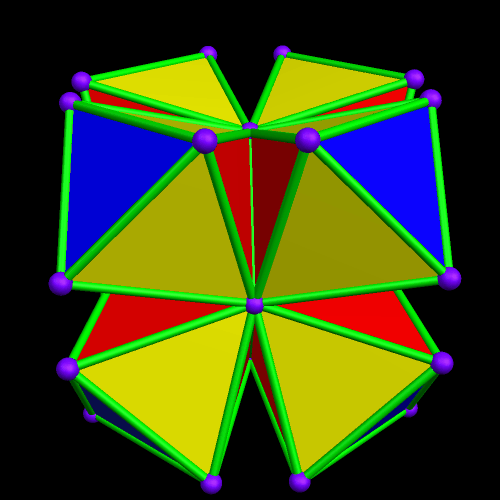
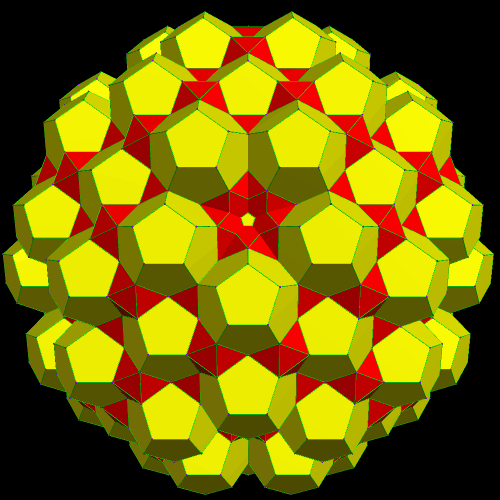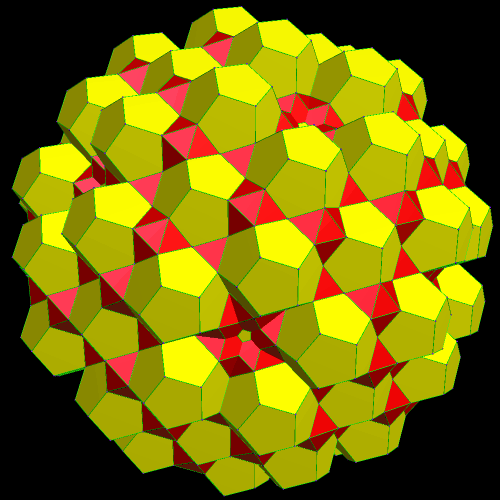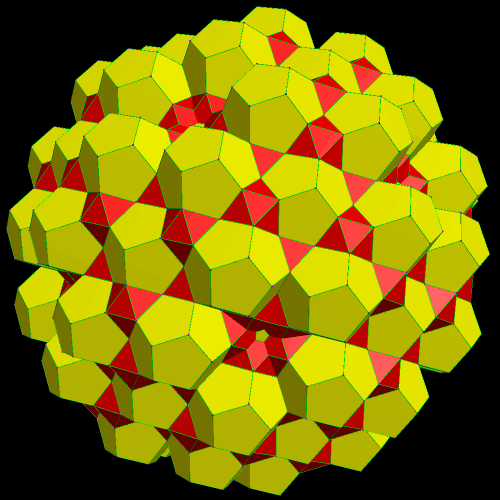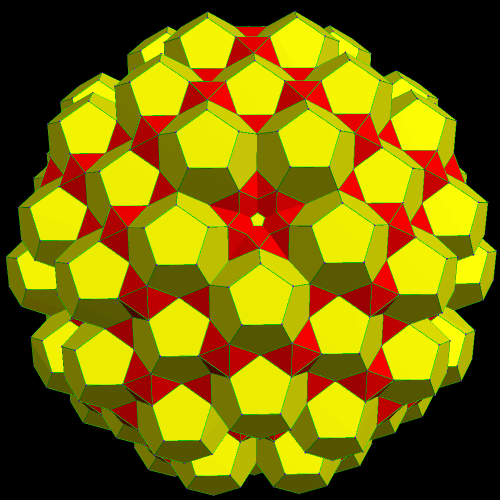
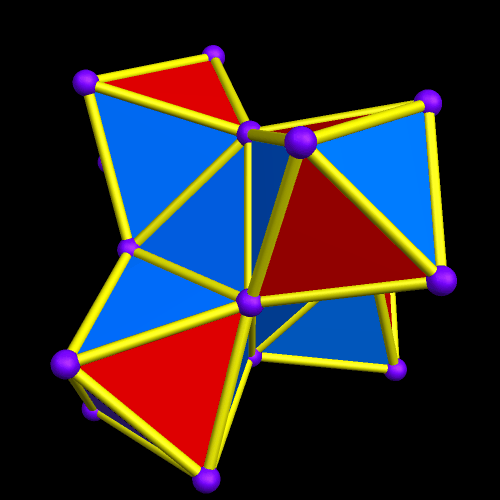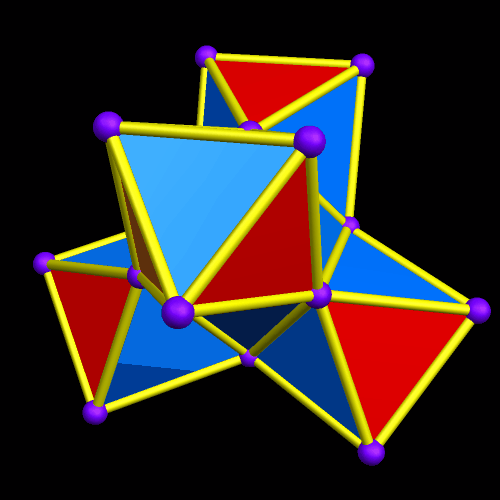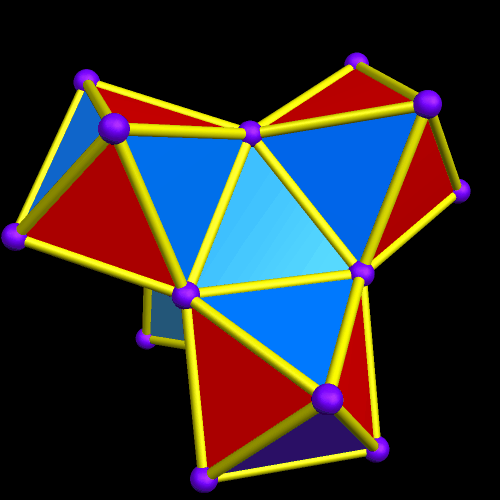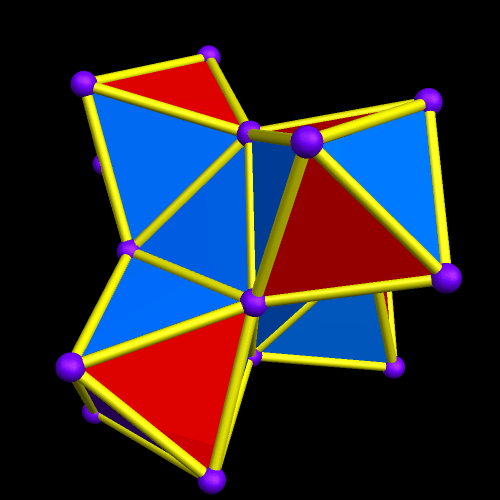
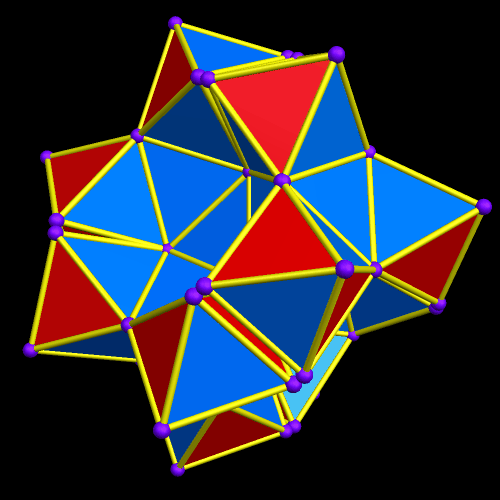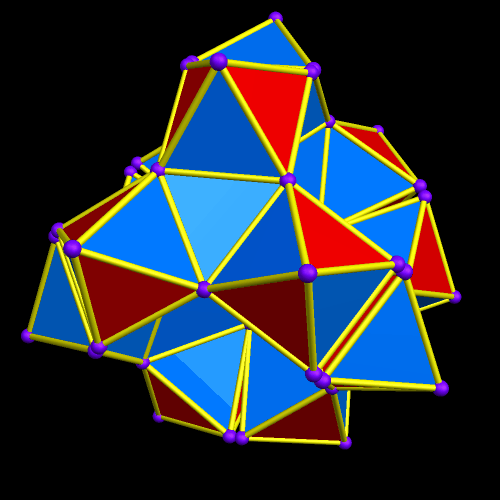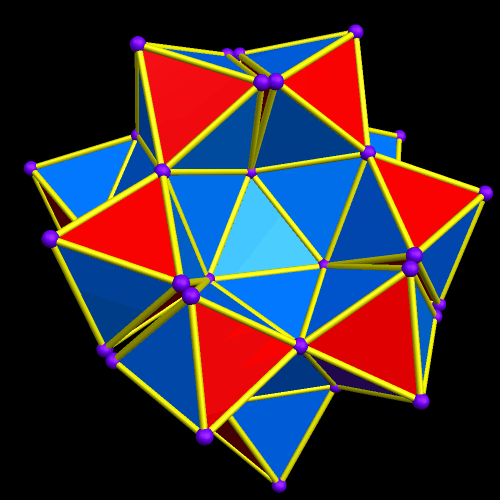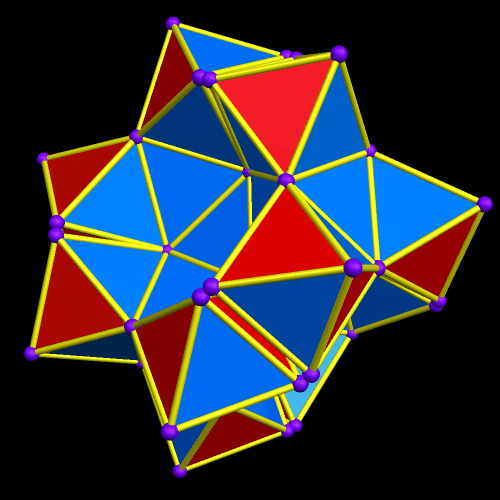
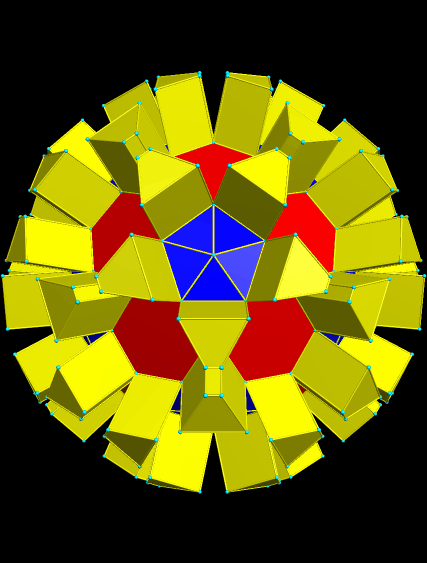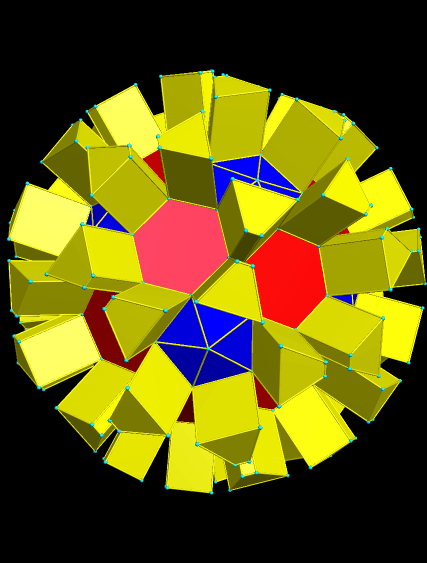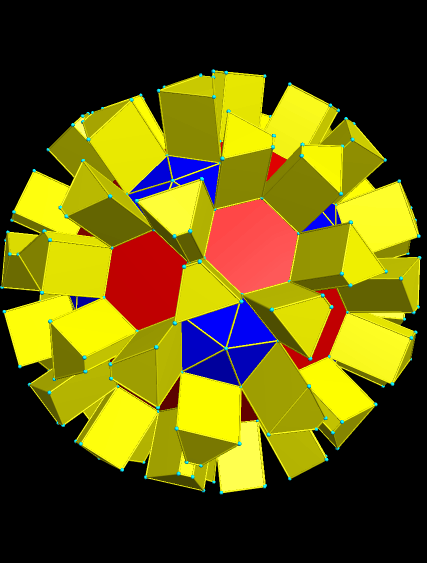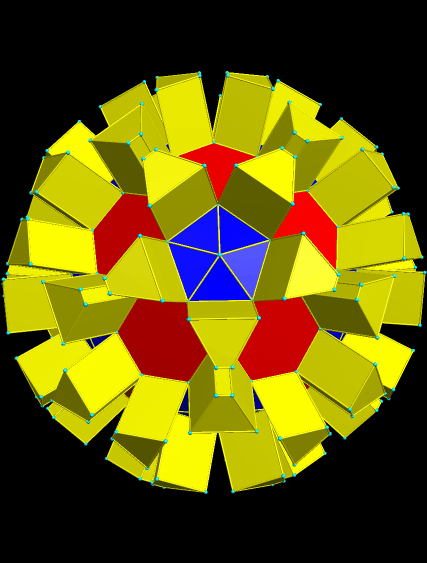
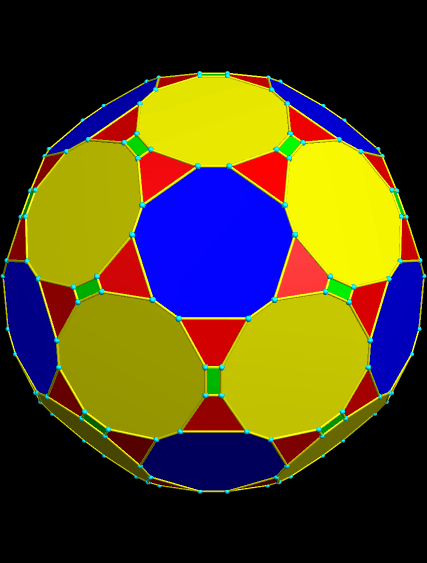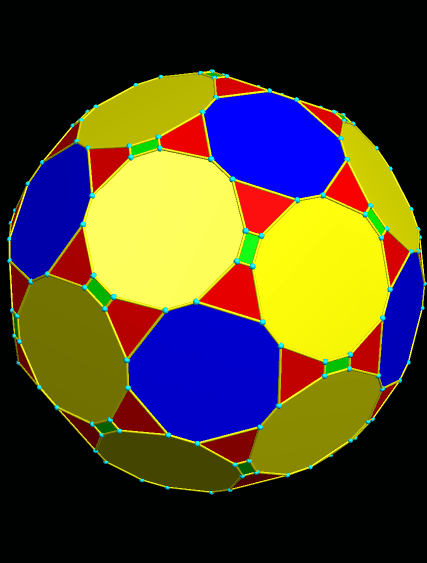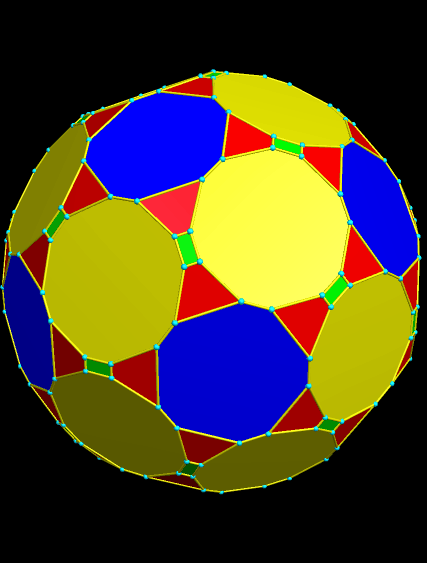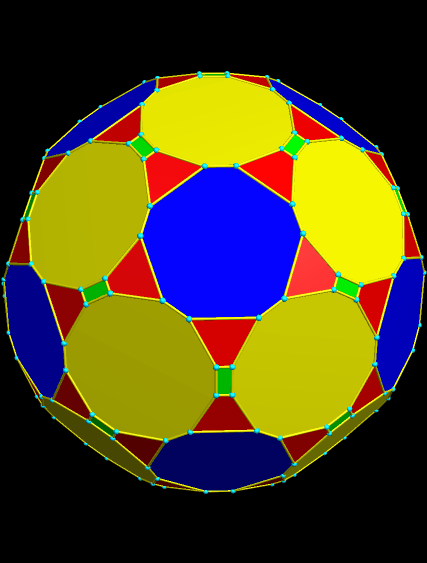
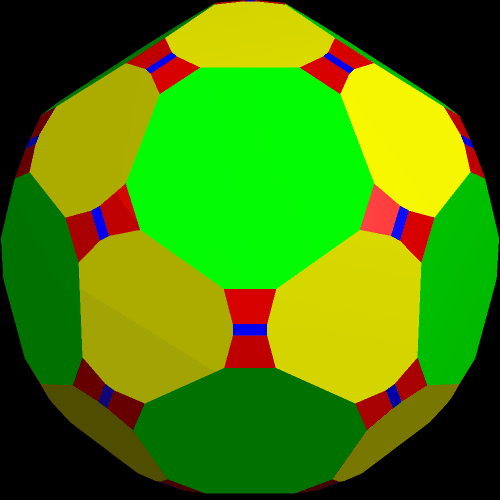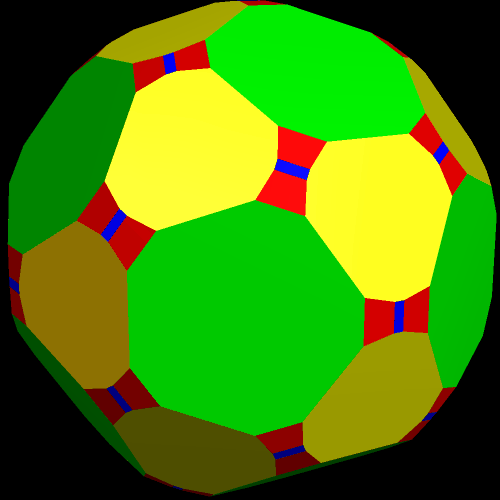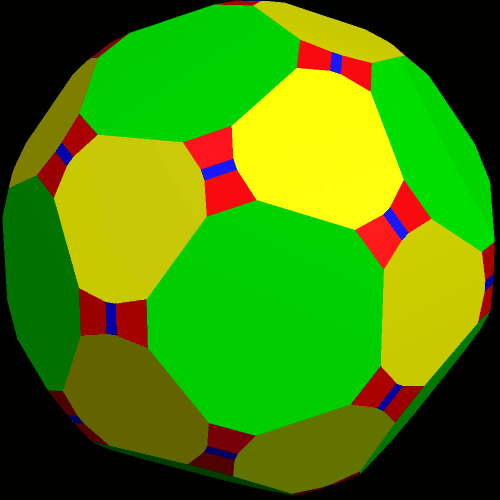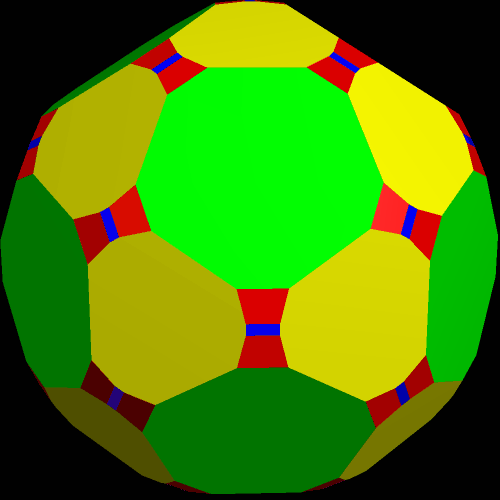
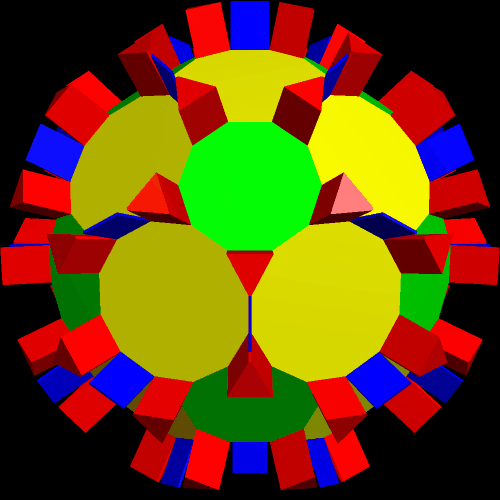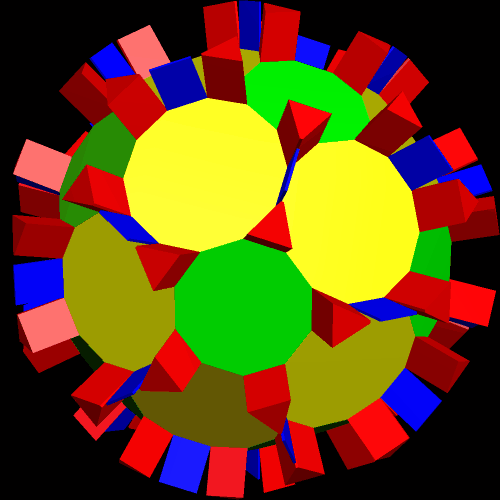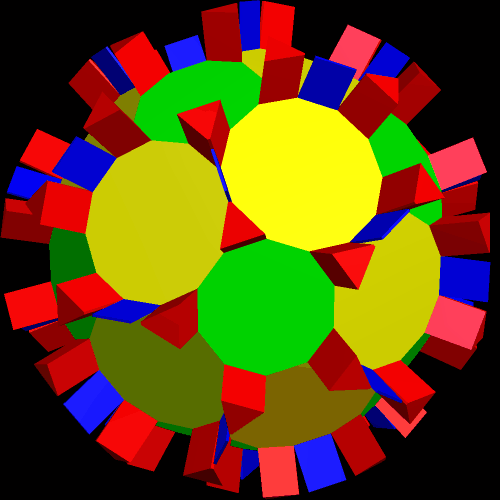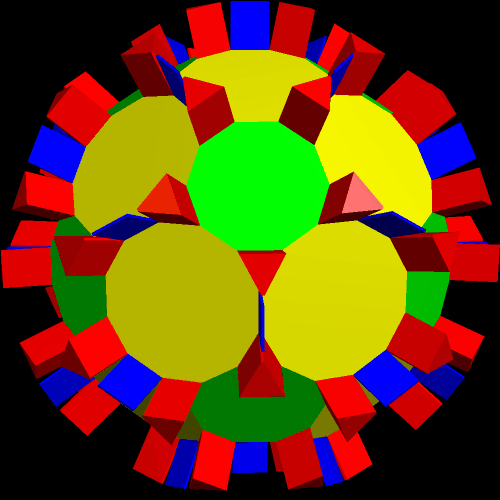
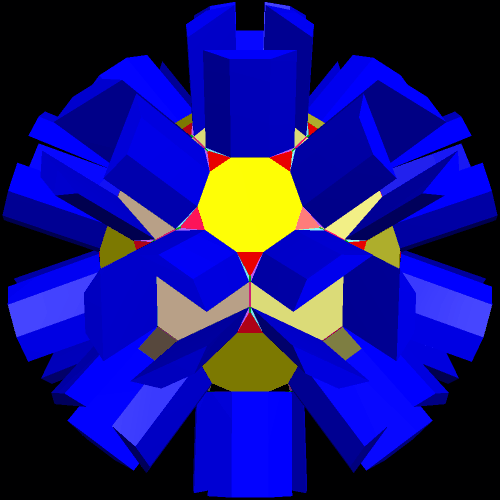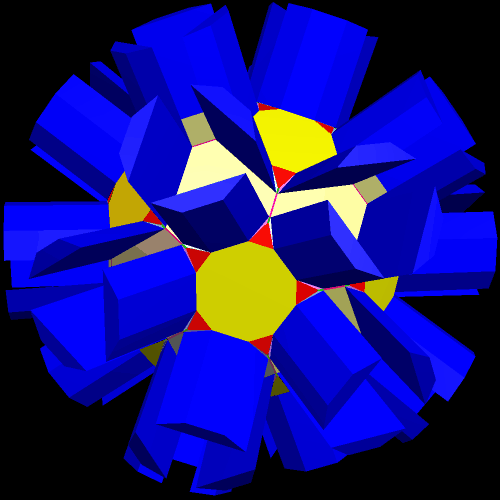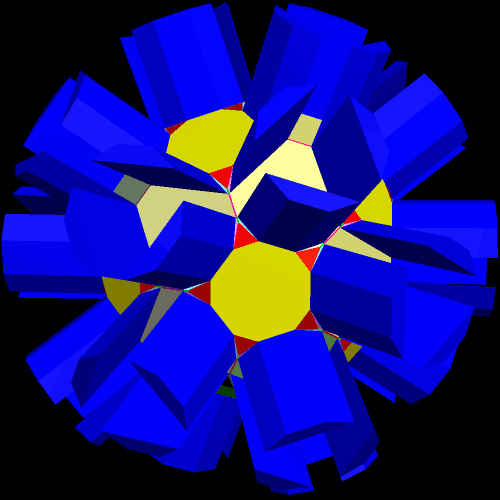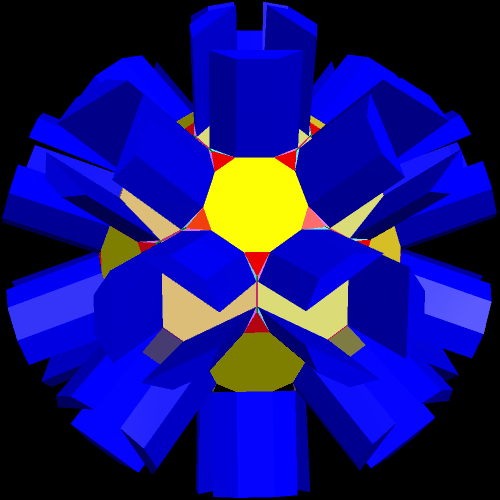
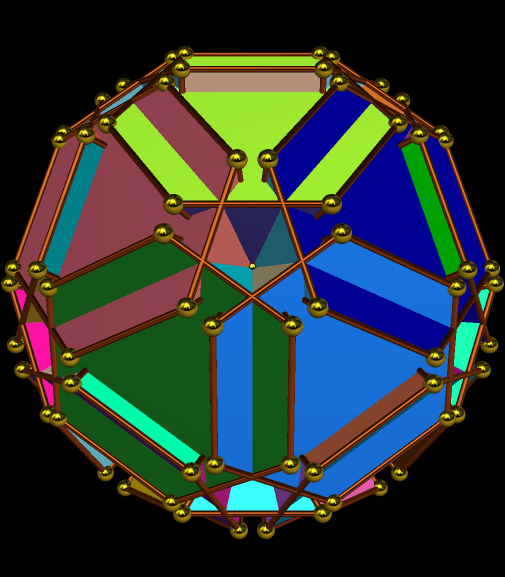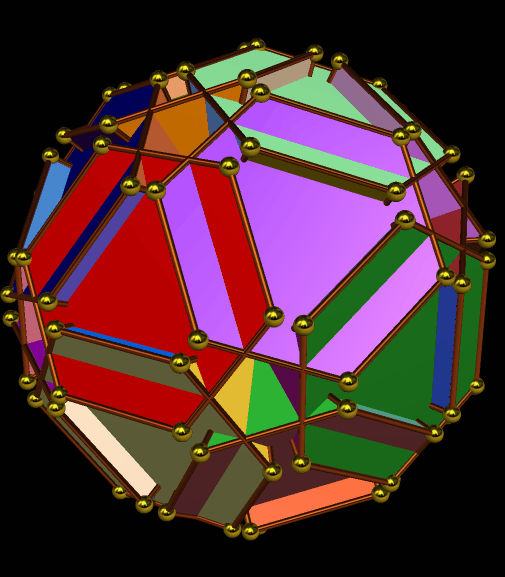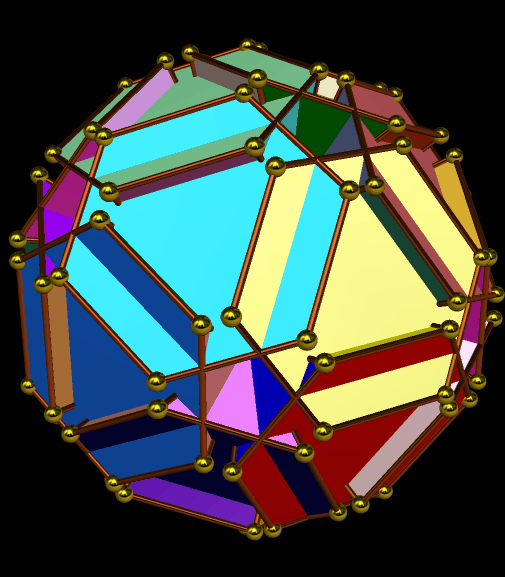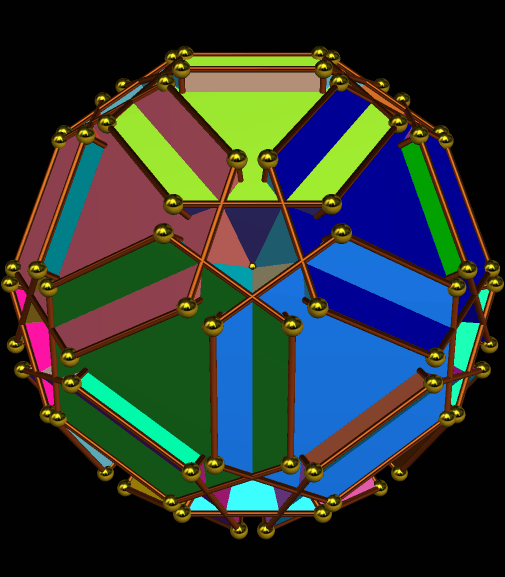
I call this variant of the rhombicosidodecahedron “greatly augmented” because it was formed by augmenting each pentagonal face of a central rhombicosidodecahedron with a great dodecahedron, while each triangular face is augmented with a great icosahedron. It was made using Stella 4d, which may be found here.
If one starts with a central truncated octahedron, leaves its six square faces untouched, and augments its eight hexagonal faces with trianglular cupolae, this is the result.
Seeing this, I did a quick check of its dual, and found it quite interesting:
After seeing this dual, I next created its convex hull.
After seeing this convex hull, I next creating its dual: one of several 48-faced polyhedra I have found with two different sets of twenty-four kites as faces, one set in six panels of four kites each, and the other set consisting of eight sets of three kites each. I think of these recurring 48-kite-faced polyhedra as polyhedral expressions of a simple fact of arithmetic: (6)(4) = (8)(3) = 24.
I use Stella 4d (available at http://www.software3d.com/Stella.php) to perform these polyhedral transformations. The last one I created in this particular “polyhedral journey” is shown below — but, unfortunately, I cannot recall exactly what I did, to which of the above polyhedra, to create it.
If one starts with a central octahedron, then augments each of its eight triangular faces with identical octahedra, this is the result.
It is then possible to augment each visible triangle of this cluster with yet more octahedra, which produces this result, in which some octahedra overlap each other.
After making this, I wanted to see its convex hull: the smallest, tightest-fitting convex polyhedron which can contain a given non-convex polyhedron. (I use Stella 4d: Polyhedron Navigator to perform these manipulations of polyhedra, and this program makes this a fast and easy process. If you’d like to try this software, even as a free trial download, the website to visit is http://www.software3d.com/Stella.php.) Here’s what this convex hull, which bears a resemblance to the rhombcuboctahedron, looks like.
Looking for previously-unseen, and interesting, polyhedra, I then starting stellating this convex hull. I did find something interesting — to me, anyway — after only two stellations.
That concluded my latest polyhedral investigation, but I certainly don’t intend it to be my last.
If one starts with a single icosidodecahedron, and then augments its pentagonal faces with dodecahedra, and its trianguar faces with icosahedra, this is the result.
This figure has gaps in it where two pentagons and two triangles meet around a vertex. If one puts icosidodecahedra in those gaps, this is the resulting figure.
Next, once again, the pentagonal faces are augmented with dodecahedra, and the triangular faces with icosahedra.
These virtual polyhedral models were all built using Stella 4d, available at http://www.software3d.com/Stella.php.
I’m going to start this experiment with a single octahedron, with faces in two colors, placed so that two faces which share an edge are always of different colors.
Next, I will augment the red faces — and only the red faces — with identical octahedra.
The regions with four blue, adjacent faces look as though they might hold icosahedra — but I checked, and they don’t quite fit. I will therefore continue the same process — augmenting only the red faces with more octahedra of the original type.
I’ve now decided that I definitely like this game, so I’ll keep playing it.
Immediately above, at the fourth of these images, some of the octahedra have started to overlap slightly, but I’m choosing to not be bothered by that — I’m continuing the now-established pattern, just in order to see where it takes me.
The regions of overlap are now far more obvious, but I’m continuing, anyway. Why? Because this is fun, that’s why! Right now, Stella 4d, the program I use to do these polyhedral manipulations, is chugging away on the next one. (This program is avilable at http://www.software3.com/Stella.php.) Ah, it’s ready — here it is!
Rather than repeat this process again, I now have another question: what would the convex hull of this figure look like? (A convex hull of a non-convex polyhedron is the smallest convex polyhedron which can contain a given non-convex polyhedron.) With Stella 4d, that’s easily answered.
I must admit this: that was nothing like what I expected — but such unexpected discoveries are a large part of what makes these polyhedral investigations with Stella 4d so much fun. And now, to close this particular polyhedral journey, I will have Stella 4d produce, for me, the dual of the convex hull shown above. (In case you aren’t familiar with duality regarding polyhedra, it describes the relationship between the octahedron, with which this post began, and the familar cube. Basically, with duals, faces and verticies are “flipped” over edges, although that is an extremely informal and imprecise way to describe the at the process.)
And with that, my friends, I bid you good night!
To begin this, I took an icosahedron, and made a zonish polyhedron with it, with the new faces based on the zones of the existing faces. Here’s the result.
Next, I started stellating the polyhedron above. At the sixth stellation, I found this. It’s a true zonohedron, and the first polyhedron shown here is merely “zonish,” because one has triangles, and the other does not. (One of the requirements for a polyhedron to be a zonohedron is that all its faces must have an even number of sides.)
After that, I kept stellating, finding this as the 18th stellation of the first polyhedron shown here.
With this polyhedron, I then made its convex hull.
At this point, the irregular hexagons were bothering me, so I used Stella 4d‘s “try to make faces regular” option. (Stella 4d is polyhedron-manipulation software you can try for free, or purchase, right here.)
The next step I chose was to augment all the yellow trapezoids with prisms, each with a height 1.6 times the trapezoids average edge length.
The next step was, again, to make the convex hull.
At this point, I tried “try to make faces regular” again, and was pleased with the result. The green rectangles became so thin, however, that I had to stop displaying the edges and vertices, in order for then to be seen.
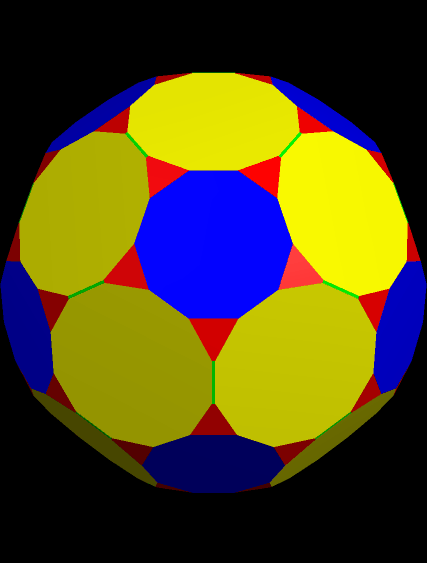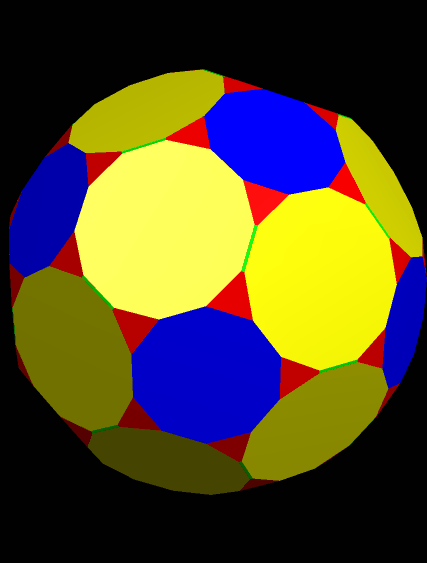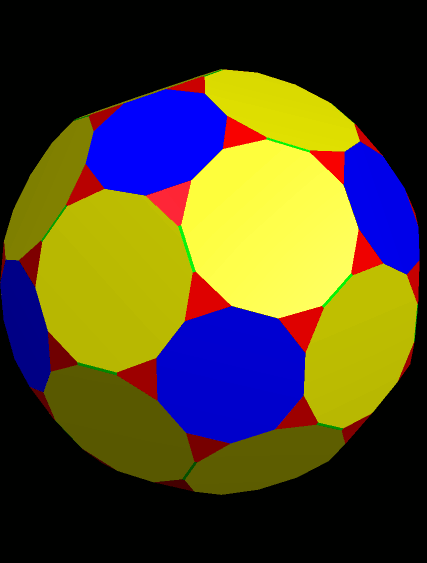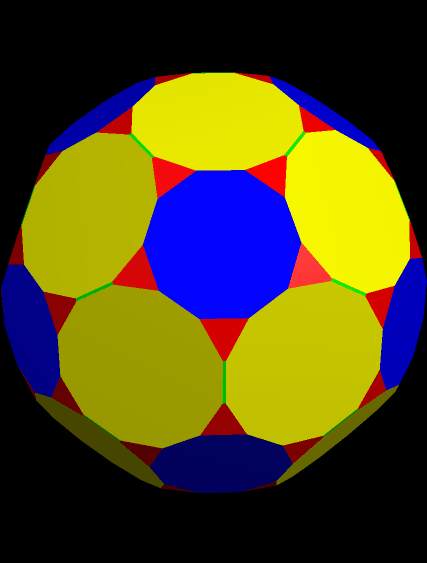Next, I augmented both the blue faces (decagons) and the yellow faces (dodecagons) with antiprisms, again using a height 1.6 times that of the augmented faces’ average edge-lengths.
Next, I made the convex hull again — a step I often take immediately after augmenting a polyhedron.
This one surprised me, as it is more complicated than I expected. To clean things up a bit, I augmented only the trapezoids (dark pink) with prisms, and dodecagons (green) with antiprisms, again using the factor 1.6 for the augmentation-height.
The next step I chose was to take the convex hull, once more. I had not yet noticed that the greater height of the trapezoidal prisms would cause the dodecagonal antiprisms to be “lost” by this step, though.
Next, “try to make faces regular” was used again.
This last result had me feeling my polyhedral journey was going in circles, so I tried augmentation again, but in a different way. I augmented this polyhedron, using prisms, on only the red trapezoids (height factor, 1.6 again) and the blue rectangles (new height factor, 2.3 times average edge length).
After that, it was time to make another convex hull — and that showed me that I had, indeed, taken a new path.
I found the most interesting faces of this polyhedron to be the long, isosceles trapezoids, so I augmented them with prisms, ignoring the other faces, using the new height-factor of 2.3 times average edge length this time.
Of course, I wanted to see the convex hull of this. Who wouldn’t?
I then started to stellate this figure, choosing the 14th stellation as a good place to stop, and making the edges and vertices visible once more.
After making the above polyhedron using Stella 4d (a program you can try for free at www.software3d.com/Stella.php), I checked its dual, which is shown below. I was surprised at its appearance, for it resembles a stellated polyhedron, even though it was created by a completely different process.
Crystals and crystalline growth have been studied for centuries because of, at least in part, their symmetry. Crystals are cut in such a way as to increase this symmetry even more, because most people find symmetry attractive. However, where does the original symmetry in a crystal come from? Without it, jewelers who cut gemstones would not exist, for the symmetry of crystalline minerals themselves is what gives such professionals the raw materials with which to work.
To understand anything about how crystals grow, one must look at a bit of chemistry. The growth of crystals:
Why small pieces? That’s easy: we live in a universe where atoms are tiny, compared to anything we can see. Why is the number of rules for combining parts small, though? Well, in some materials, there are, instead, large numbers of ways that atoms, etc., arrange themselves — and when that happens, the result, on the scale we can see, is simply a mess. Keep the number of ways parts can combine extremely limited, though, and it is more likely that the result will possess the symmetry which is the source of the aesthetic appeal of crystals.
This can be modeled, mathematically, by using polyhedral clusters. For example, I can take a tetrahedron, and them augment each of its four faces with a rhombicosidodecahedron. The result is this tetrahedral cluster:
Next, having chosen my building blocks, I need a set of rules for combining them. I choose, for this example, these three:
Using these rules, the first augmentation produces this:
That, in turn, leads to this:
Next, after another round of augmentation:
One more:
In nature, of course, far more steps than this are needed to produce a crystal large enough to be visible. Different crystals, of course, have different shapes and symmetries. How can this simulation-method be altered to model different types of crystalline growth? Simple: use different polyhedra, and/or change the rules you select as augmentation guidelines, and you’ll get a different result.
[Note: all of these images were created using Stella 4d: Polyhedron Navigator. This program is available at http://www.software3d.com/Stella.php.]
I made these using Stella 4d, which you can try at http://www.software3d.com/Stella.php. Here is its dual, also:
To make this polyhedron using Stella 4d: Polyhedron Navigator (a program which is available at this website), I started with an icosidodecahedron, augmented all faces with prisms of height 1.6 times greater than their bases’ edge length, and then took the convex hull of the result. I’m proposing it as a candidate for the loosely defined group of polyhedra called near-misses to the 92 Johnson solids: convex polyhedra which are almost, but not quite, Johnson solids, due to slight irregularity in some of their faces.
In this case, the pentagons and green triangles are regular, and have the same edge length. The blue triangles, however, are isosceles, with vertex angles of ~67.6687 degrees. The yellow almost-squares are actually rectangles, with edges next to blue triangles which are ~2.536% longer than the edges next to pentagons or green triangles.
I stumbled upon this design earlier today, while simply exploring polyhedra more-or-less randomly, using Stella. Below is the prototype I found at that time, which I merely made a .gif of, but did not perform measurements on.
In this prototype, the most significant difference I can detect is in the yellow faces, which are trapezoids, rather than rectangles, since the pentagon edge-length is slightly longer than that of the green triangles.
Stella has a “try to make faces regular” function built-in to try to help improve upon polyhedra such as these, but here’s what happens when that function is used on the first polyhedron shown above:
Behold! It worked — all of the faces are perfectly regular. However, that caused another problem to appear, and you can see it most easily by looking at the blue triangle-pairs: this polyhedron is slightly non-convex. It’s also easily described as a truncated dodecahedron, with each of the twelve decagonal faces augmented by a pentagonal rotunda.
I’ll show this to some other people who are polyhedron-experts, and will update this post with what I find after I’ve talked to them. My questions for them, as usual in such situations, are two in number:
1. Has this polyhedron been found before?
2. Is it close enough to regularity to qualify for “near-miss” status?
If it hasn’t been found before, but is judged unworthy of “near-miss” status, it will at least join the newly-described group I call “near near-misses” — polyhedra which don’t quite qualify for near-miss status, by visual inspection. Obviously, this new group’s definition is even more “fuzzy” than that of the near-misses, but there is a need for such a category, nonetheless.
[Update: Robert Webb, who wrote Stella 4d (and is not the blogger here, despite our sharing a first name), has seen this before, so it isn’t an original discovery of mine. He doesn’t accept it as a near-miss on the grounds that it naturally “wants” to be non-convex, as seen in the last of the three images in this post, and I agree with his reasoning. I’m therefore considering this to be a “near-near-miss.”]
RobertLovesPi.net 