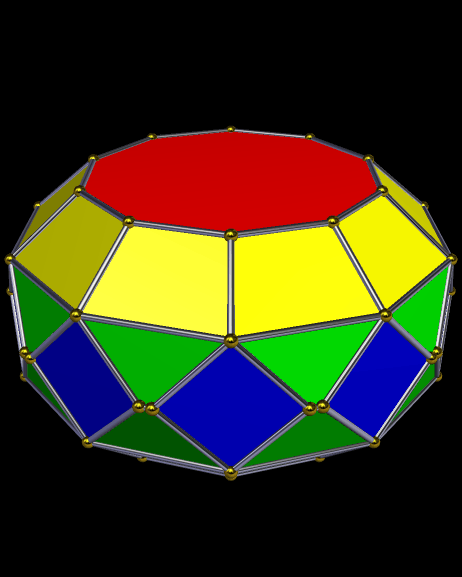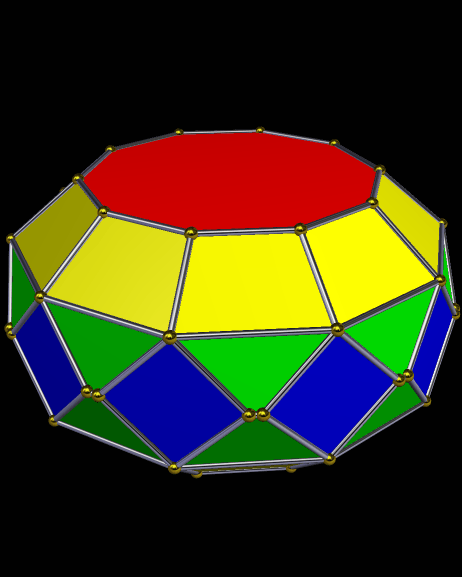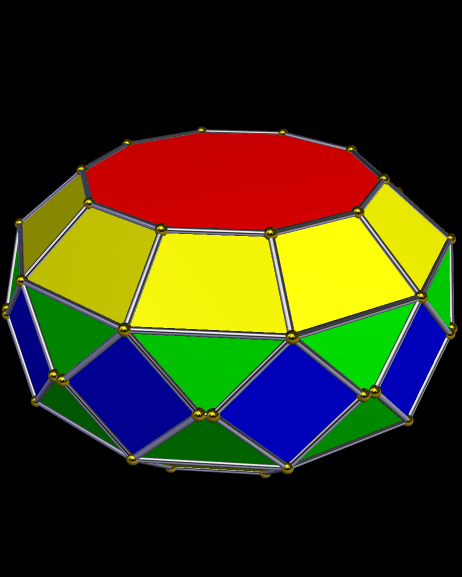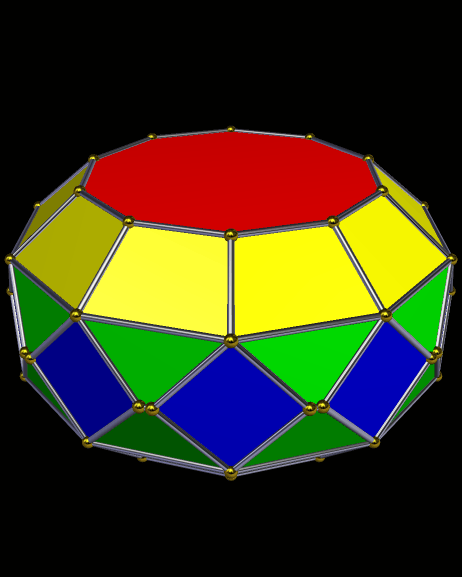
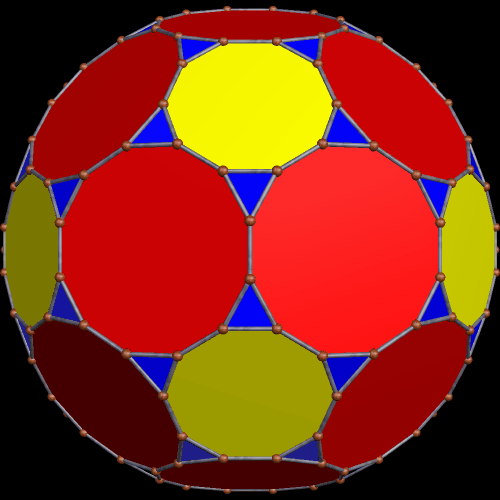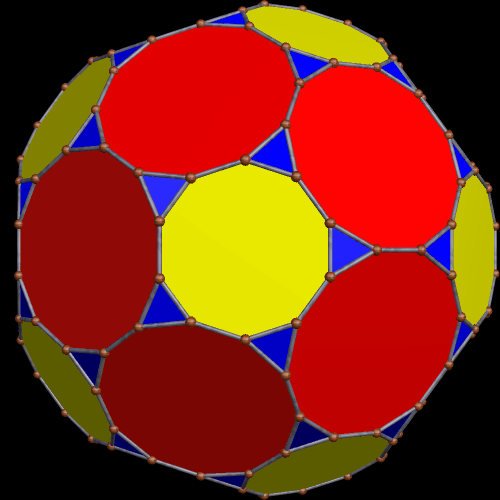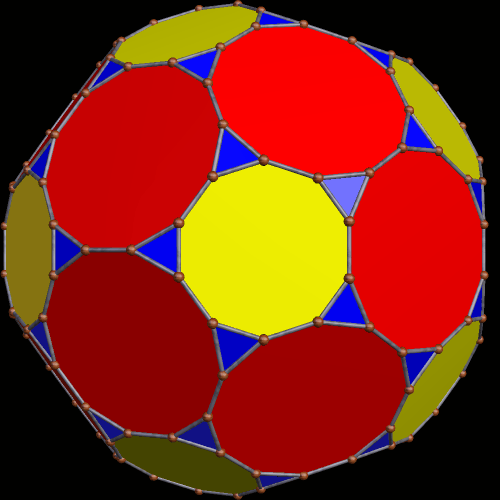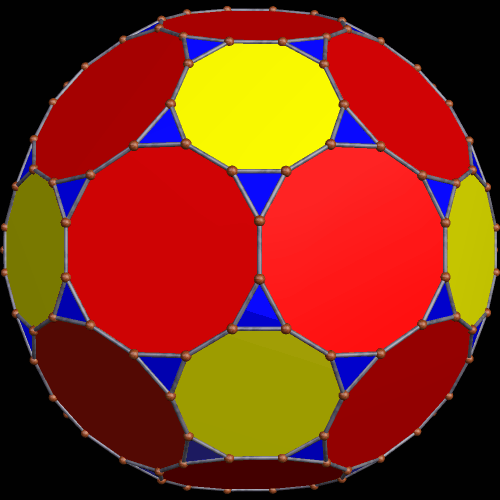
The twelve purple faces of this faceted dodecahedron show up on Stella 4d‘s control interface as {10/4} star decagons, which would make them each have five pairs of two coincident vertices. I’m informally naming this special decagon-that-looks-like-a-pentagram (or “star pentagon,” if you prefer) the “antipentagram,” for reasons which I hope are clear.
Stella 4d, the program I use to make most of my polyhedral images, may be tried for free at http://www.software3d.com/Stella.php.
This tiling-pattern could be continued indefinitely, while still maintaining its five-fold radial symmetry, giving it the overall appearance of a pentagon.
The golden triangles, in yellow, are acute isosceles triangles with a leg:base ratio which is the golden ratio. Golden gnomons, shown in orange, are related, for they are obtuse isosceles triangles where the golden ratio shows up as the base:leg ratio, which is the reciprocal of the manifestation of the golden ratio which appears in the yellow triangles.
The icosahedron has twenty triangular faces. Truncate it once, and the triangles become hexagons, with pentagons appearing under the pyramids removed in the truncation. This is the “soccer ball” shape familiar to millions.
If you take this figure and truncate it again, the twenty hexagons become twenty dodecagons, the twelve pentagons each become decagons, and sixty isosceles triangles appear under the pyramids removed by this second truncation.
I made this image using Stella 4d, a program you can find at www.software3d.com/Stella.php. Also, just for fun, here’s a version of it with the colors switched around, and with a slight bounce as it rotates in the other direction.
Each pair is a different color. Because these decagons intersect in space, but do not meet at edges, they do not form a true polyhedron. They are merely a symmetrical configuration of twelve decagons in space, surrounding a central point.
I made this out a “true polyhedron” by hiding all the other faces from view. Before the hiding and recoloring of faces, this looked this way (you can click on it to enlarge it):
I used Stella 4d to make these images, and you can find that program at http://www.software3d.com/Stella.php.
I created this using Stella 4d: Polyhedron Navigator, a program you can find athttp://www.software3d.com/Stella.php.
RobertLovesPi.net 