Foldable Snake Toys, of Two Sizes, and the Polyhedra You Can Make With Them

Posted on 19 March 2025 by RobertLovesPi

This is the familiar “magic snake” toy, which has been around for many years. The most common version of it is made of 24 right triangular prisms. It can be twisted into many different shapes.

Of course, me being me, I wanted to make polyhedra with these snake-toys. Here are three of these standard-sized toys, twisted into rhombicuboctahedra.

While it isn’t easy, it is possible to find longer variants of this toy. I found one on Amazon which is made of 72 prisms, making it three times the standard length. In this picture, the extra-long snake appears on the top, while below it are the three smaller ones, laid end-to-end.

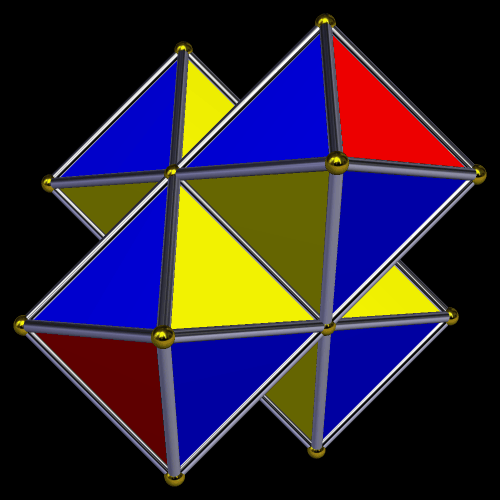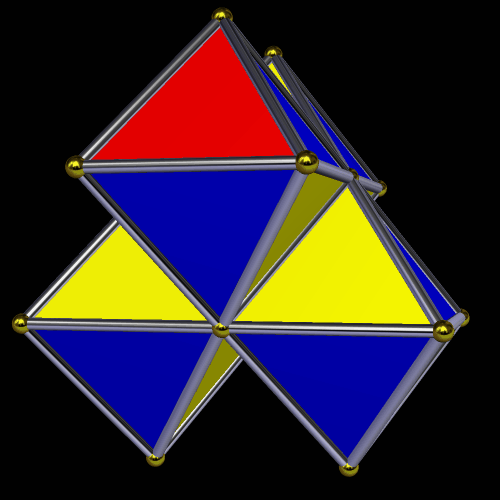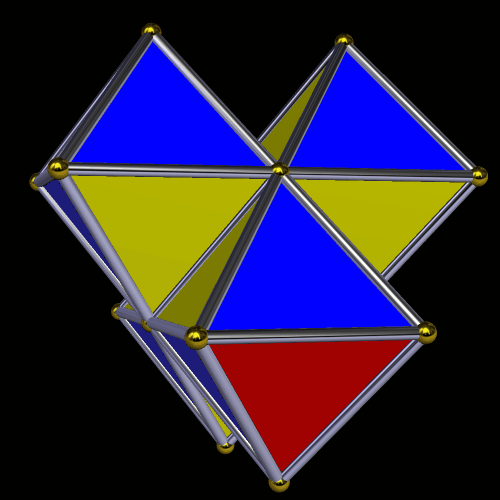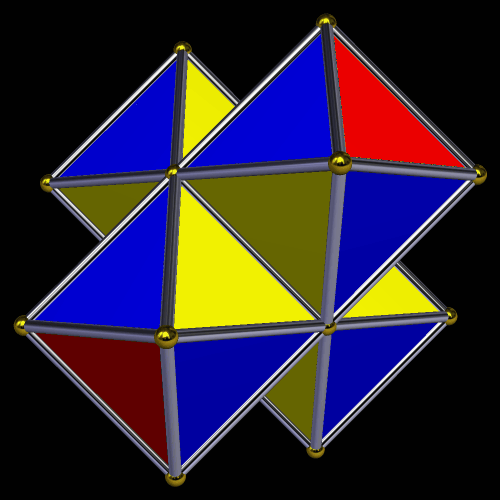
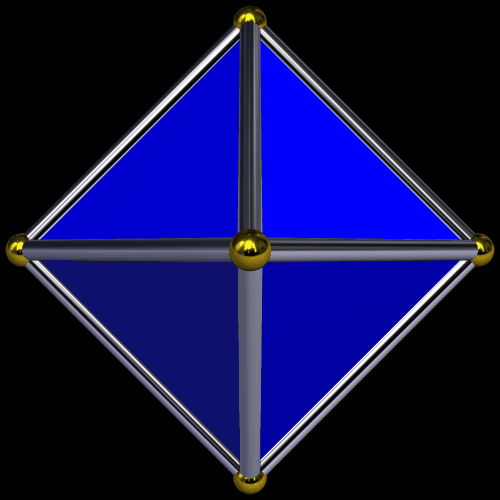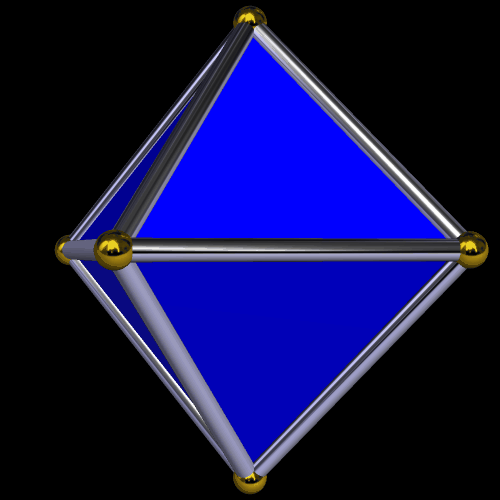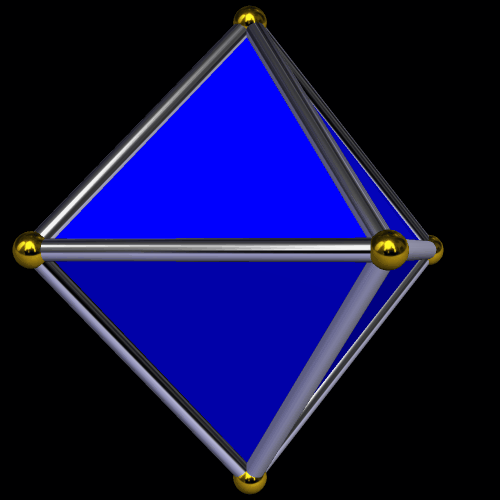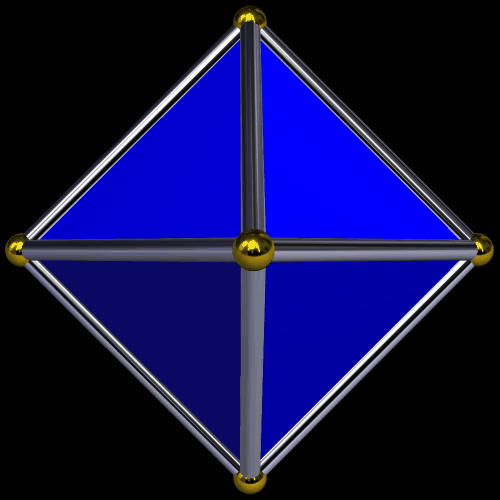
When I started playing with the longer one, I tried to make it into a symmetric polyhedron, and found doing so quite a challenge . . . but, in the end, I prevailed, by twisting it into a hollow octahedron.

This longer version may be found here on Amazon, in case you’d like to get one of your own. The smaller ones are easy to find (just search for “magic snake toy math”), and cost a lot less. I’m glad to have both sizes in my collection of geometric toys.

Five Views of the Compound of the Truncated Cube and the Truncated Octahedron

Posted on 30 October 2024 by RobertLovesPi

When I first made this compound using Stella 4d (available here), these are the colors the software automatically selected.

I wanted to find a better coloring-scheme, so I told Stella to color the model as a compound. Here’s what I got.

Next, I tried “color by face type.” This yields four colors, instead of just two.

I then tried “rainbow color mode,” with this result.

One more try (color by face, unless the faces are parallel) gave me my favorite color scheme for this compound.

Which one do you like best?

The Compound of Ten Octahedra and Its Dual, the Compound of Ten Cubes

Posted on 25 September 2021 by RobertLovesPi

I stumbled upon the compound above while playing with facetings, starting with the rhombic triacontahedron. Here’s the compound’s dual.

I made these rotating models using Stella 4d, a program you can try for free at this website.

Four Octahedra

Posted on 11 May 2021 by RobertLovesPi

There’s a tetrahedron in the center of this figure, but you can’t see it because it is covered on all sides by octahedra. I made this using Stella 4d, which you can try for free at this website.

Here’s another version, with a different coloring-scheme.

Augmenting, then Reaugmenting, the Octahedron

Posted on 3 May 2021 by RobertLovesPi

The blue figure above is an octahedron. The next image shows what happens if red octahedra are used to augment each of the blue octahedron’s faces.

The third image shows what happens if yellow octahedra are used to augment each red face in the second figure.

These polyhedral images were created using Stella 4d: Polyhedron Navigator, which you can try for free at http://www.software3d.com/Stella.php.

Improved Lux Octahedron

Posted on 11 May 2020 by RobertLovesPi

The first Lux Blox model I posted on this blog was an octahedron. After a little more practice, though, I have an improved model of this polyhedron to show here.

Lux are for sale at http://www.luxblox.com.

An Octahedron Made of Lux Blox

Posted on 2 May 2020 by RobertLovesPi

This is the first model I built with Lux Blox, a modeling-system I’ve been checking out. If you’d like to try Lux for yourself, the website to visit to get them is https://www.luxblox.com/.

This is an octahedron with an edge length of two. The eight triangular faces are blue, while the edges of the octahedron are orange. Apart from their colors, all these pieces are identical — the basic Lux block, also known as a Lux square. With just this one block, you can build literally millions of things. I’m into polyhedra, so that’s what I’ll be building a lot of, but someone obsessed with dinosaurs could build models of those, as well. Lux Blox are that versatile.

The images above and below show the same Lux polyhedron, viewed from different angles.

Filling Space with Cuboctahedra and Octahedra

Posted on 18 March 2020 by RobertLovesPi

To get started packing space with cuboctahedra and octahedra, I started with a single octahedron, then augmented its square faces with additional cuboctahedra.

Next, I augmented each triangular face with a blue octahedron.

Next, I augmented each square face with a cuboctahedron.

Next, I added still more cuboctahedra.

The next step was to augment the yellow triangular faces with blue octahedra.

I next added more cuboctahedra.

This process may be continued without limit. I used a program called Stella 4d to make these models, and you can try this software yourself, for free, at this website.

A Compound of Three Elongated Octahedra

Posted on 14 March 2020 by RobertLovesPi

This compound is the 16th stellation of the tetrakis hexahedron, the Catalan solid which is the dual of the Archimedean truncated octahedron. I made it using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.

Spectral Octahedra

Posted on 1 February 2020 by RobertLovesPi

Stella 4d: Polyhedron Navigator has a “put models on vertices” function which I used to build this complex of octahedra. If you’d like to try this software for yourself, there is a free trial version available at http://www.software3d.com/Stella.php.