Unlike my previous octagon-tiling discoveries (see previous post), this is a chiral, radial tessellation, with the colors chosen to highlight that fact.
Octagons Can Tile a Plane III
4
Tag Archives: plane
Octagons Can Tile a Plane II
In April 2014, I found a tessellation of the plane which uses two kinds of octagons — both types equilateral, but only one type regular.
Now, I have found two more ways to tessellate a plane with octagons, and these octagons are also equilateral. However, in these new tessellations, only one type of octagon is used. One of them appears below, twice (the second time is with reversed colors), and the other one appears, once, in the next post.
A Chiral Tessellation, Using Regular Dodecagons, Regular Hexagons, Squares, and Rhombi (from 2012)
I have several “lost works” that I’m slowly finding and posting, from old jumpdrives, computers, little-known blogs, etc., and this is one of them. I made it in 2012, but few have seen it before now.
Five Versions of a Tessellation Using Squares and Equilateral Triangles
Image
I used four other color-schemes with this same tessellation, and those other images are shown below.
Tessellation Using {8/3} Star Octagons and Squares
Image
The tessellation of the plane which uses regular convex octagons and squares is well-known. This related tessellation, however, is not. I didn’t know it existed until I stumbled across it . . . although I very much doubt I am the first person to do so.
Three-Color Tessellation: A Modification of the Tiling of the Plane with Regular Hexagons
Image
In each case, modifications along hexagon-edges were made using equilateral triangles. Every segment in this tessellation has equal length, also, which required trisection of the original hexagons’ sides.
Circumslices
Image
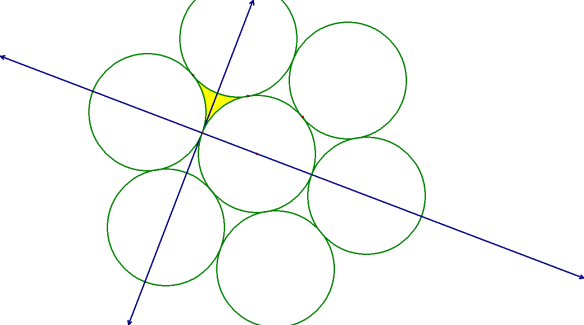
Regions between close-packed circles of equal radius resemble triangles, but with 60 degree arcs replacing the sides. As these regions are the only things left of a plane after all such circles are sliced out, and they each are outside all the circles used, I’ve decided to name them “circumslices.” Interestingly, the three interior angles of a circumslice each asymptotically approach zero degrees, as one approaches circumslice-vertices, which are also the points of contact of the circles.
Why did I name these things “circumslices?” Because they needed a name, that’s why!
A Tessellation Featuring Regular Heptagons
Image
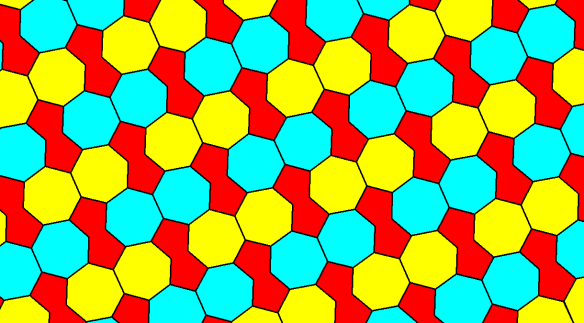
Regular heptagons, of course, can’t tile a plane by themselves. Of all tessellations of the plane which include regular heptagons, I think this is the one which minimizes between-heptagon gap-size (the parts of the plane outside any heptagon). However, I do not have a proof of this. The shape of each of the polygons which fill the “heptagon-only gaps” is a biconcave, equilateral octagon. With these octagons, this is a tessellation, but without them, it wouldn’t fit the definition of that term.
[Later edit: on Facebook, a friend showed me two others with smaller gap-sizes. In other words, the conjecture above has now been shown to be wrong.]
An Odd Tiling of the Plane
Image
An exploration of one way to surround points with hexagons, triangles, and squares.
RobertLovesPi.net 