This contains twelve octagons, six squares, and eight triangles. The “holes” in it keep it from being a true polyhedron, but it is my hope than further study of this arrangement may lead to the discovery of new, interesting, and symmetrical polyhedra.
(Image created with Stella 4d — software you can try yourself at http://www.software3d.com/Stella.php.)
There are sixty of the irregaular, pentagonal gaps. Also, the hexagons themselves are of three types, two of which are sixty in number, and one of which is thirty in number.
If the gaps are filled, and the color scheme changed to make each of the four polygon-types into its own color-group, this looks, instead, like this (click on it if you wish to see it enlarged). It has 210 faces.
(Images created with Stella 4d — software you can try yourself at http://www.software3d.com/Stella.php.)
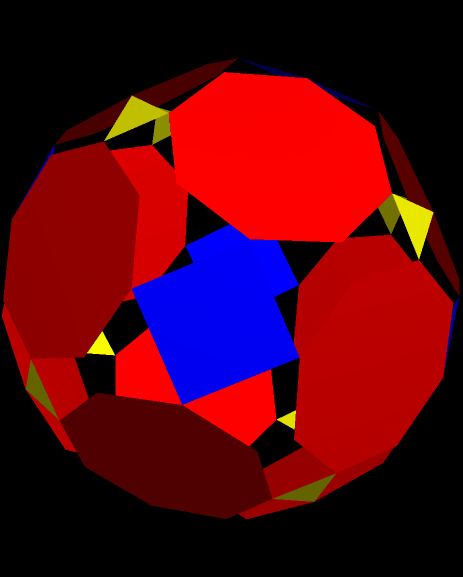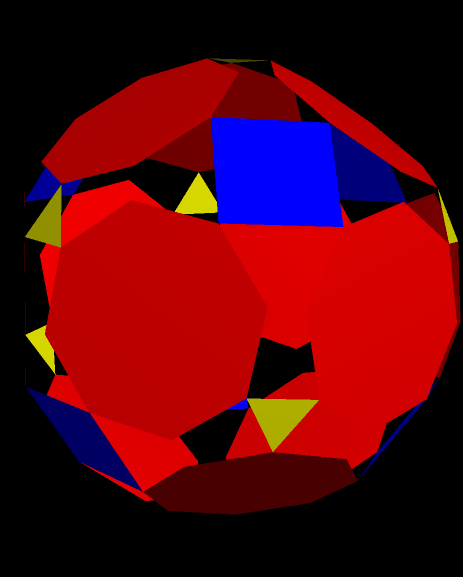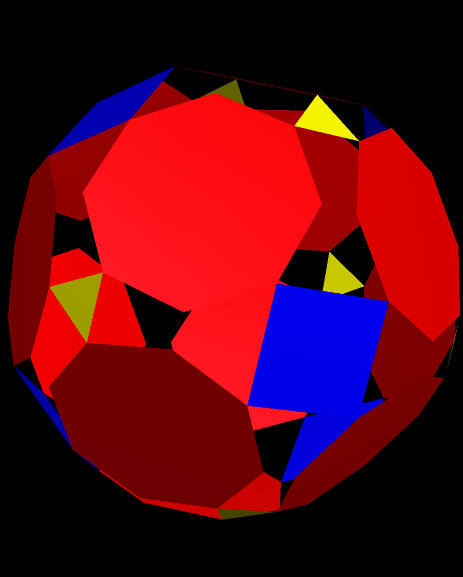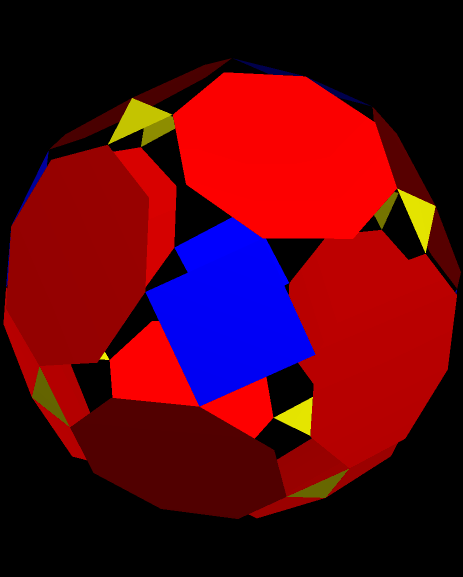
Hexacontakaihexagons have 36 sides, and dodecagons, of course, have twelve. When a regular hexacontakaihexagon is surrounded by twelve regular dodecagons, in the manner shown here, adjacent dodecagons almost, but not quite, meet at vertices. The gaps between these near-concurrent vertices are so small that they cannot be seen in this diagram — a zoom-in would be required, with thinner line segments used for the sides of the regular polygons.
As a result, the yellow and purple concave polygons aren’t what they appear, at first, to be. They look like triconcave hexagons, but this is an illusion. The yellow ones, in sets of two regions that aren’t quite separate, are actually tetraconcave, equilateral dodecagons with a very narrow “waist” separating the two large halves of each of them. As for the purple ones, they appear to occur in groups of four — but each set of four is actually one polygon, with three such narrow “waists” separating four regions of near-equal area. These purple polygons are, therefore, equilateral and hexaconcave icosikaitetragons — that is, what most people would call 24-gons.
Concave triangles do not exist, so concavity does not appear in the examination of polygons by ascending side length until the quadrilateral. A quadrilateral may only have one concavity, as shown in the red figure. Any polygon with exactly one concavity is called a uniconcave polygon.
Beginning with pentagons, the potential for two concavities appears. A polygon with two concavities, such as the yellow pentagon shown here, is a biconcave polygon.
Triconcave polygons, such as the blue hexagon here, have exactly three concavities. It is not possible for a triconcave polygon to have fewer than six sides.
For a tetraconcave polygon, with four concavities, at least eight sides are needed. The example shown here is the green octagon.
For higher number of concavities, simply double the number of sides to find the minimum number of sides for such a polygon. This pattern begins on the bottom row in the diagram here, but does not apply to the polygons shown in the top row.
The octagonal design on each face appears in the last post here, and was made using both Geometer’s Sketchpad and MS-Paint. After cropping this image, I projected it onto the faces of this polyhedron, the rhombic triacontahedron, using Stella 4d, a program you can try for yourself at http://www.software3d.com/php.
RobertLovesPi.net 