I stumbled across this compound yesterday, an example of exploratory polyhedral manipulation using Stella 4d producing an unexpected result. If you would like to experiment with a free trial download of this program, before deciding whether or not to purchase the fully-functioning version, simply click here: www.software3d.com/Stella.php.
Monthly Archives: August 2014
A Faceting of the Snub Dodecahedron
The snub dodecahedron is chiral, meaning it appears in left- and right-handed forms. This faceted version, where the same set of vertices is connected in different ways (compared to the original), possesses the same property.
Chiral polyhedra can always be tranformed into interesting polyhedral compounds by combining them with their own mirror-images. If this is done with the polyhedron above, you get this result, presented with a different coloring-scheme.
Both of these images were created using Stella 4d: Polyhedron Navigator, and you may try it at www.software3d.com/Stella.php.
Four Stellations of the Truncated Icosahedron
The truncated isocahedron has an interesting (and long) stellation series. Here are some of the stellated forms of this polyhedron which I find particularly interesting and attractive, starting with its 41st stellation.
This one is the 42nd stellation:
Jumping far ahead in the series, this is the 126th stellation:
And, finally, the 148th stellation.
All four images were produced using Stella 4d: Polyhedron Navigator. You can try this program for yourself at www.software3d.com/Stella.php.
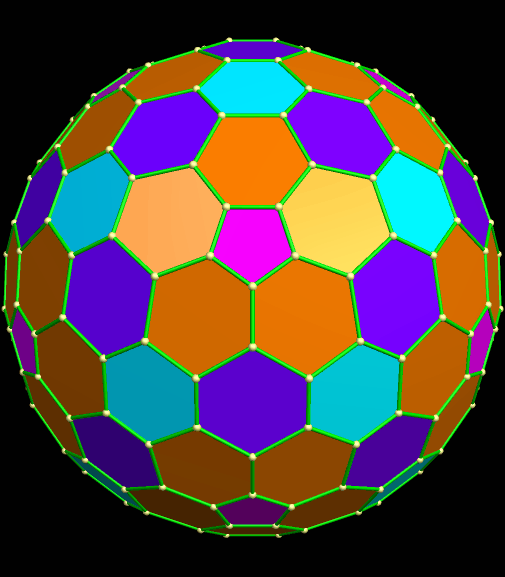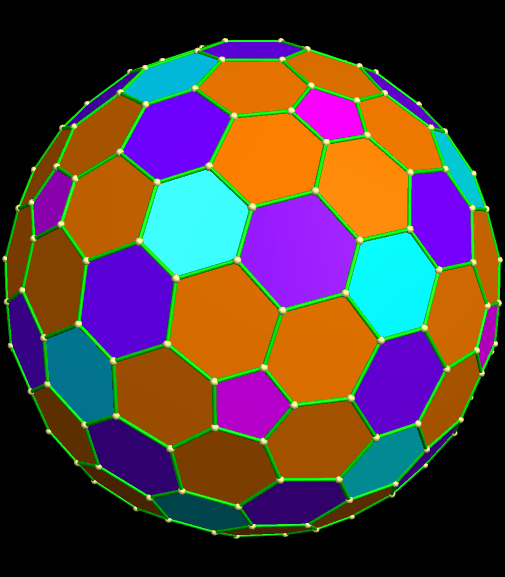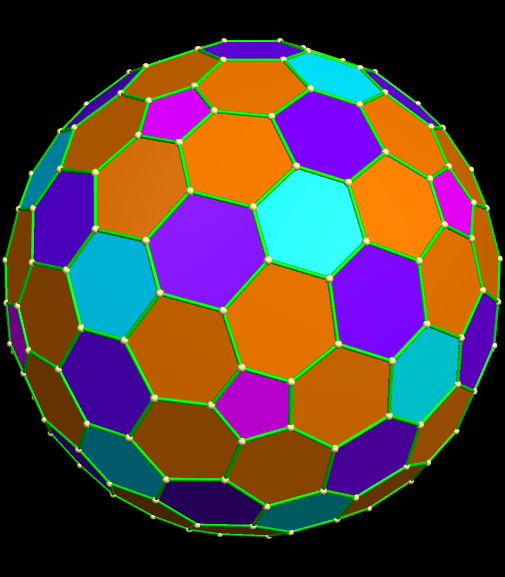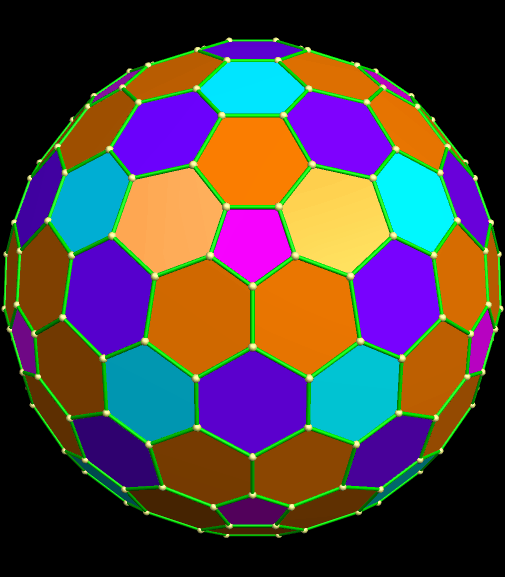
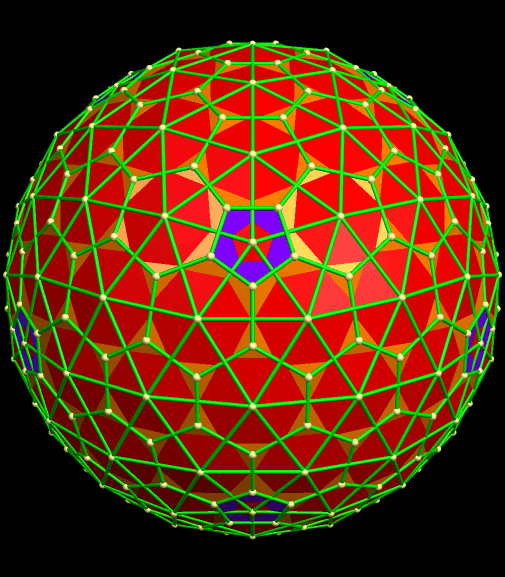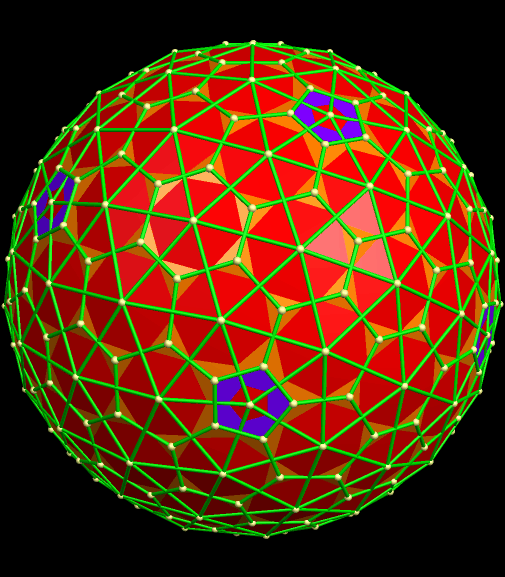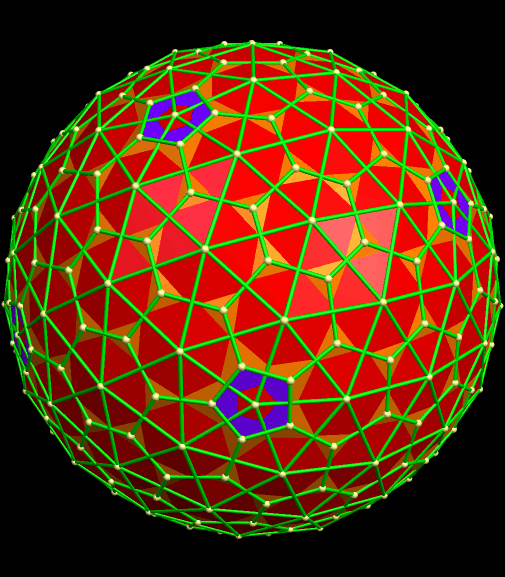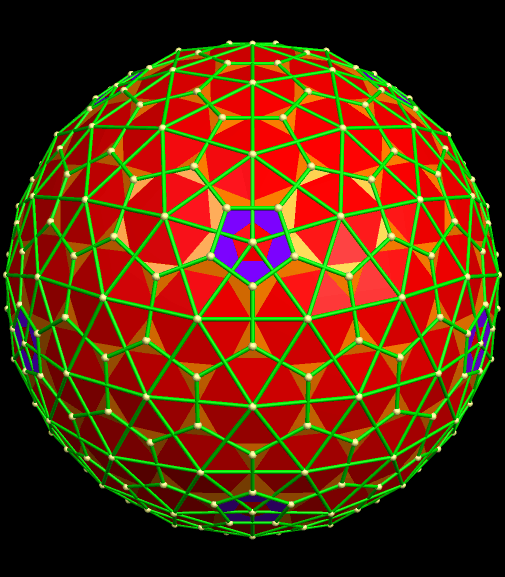
A 240-Atom Fullerene, and Related Polyhedra
The most well-known fullerene has the shape of a truncated icosahedron, best-known outside the world of geometry as the “futbol” / “football” / “soccer ball” shape — twenty hexagons and twelve pentagons, all regular. The formula for this molecule is C60. However, there are also many other fullerenes, both larger and smaller. One of my favorites is C240, simply because I sometimes make class projects out of building fullerene models with Zome (available at www.zometool.com), and the 240-atom fullerene is the largest one which can be built using Zome. Here’s what it looks like, as molecular models are traditionally colored.
This polyhedron still has twelve pentagons, like its smaller “cousin,” the truncated icosahedron, but far more hexagons. What’s more, these hexagons do not have exactly the same shape. If this is re-colored in the traditional style of a polyhedron, rather than a molecule, it looks like this. In this image, also, the different shapes of hexagons each have their own color.
Like other polyhedra, a compound can be made from this polyhedron and its dual. In this case, the dual’s faces are shown, below, as red triangles. The original fullerene-shape is in purple for the pentagonal faces, and orange for the hexagons.
In the base/dual compound above, it can be difficult to tell exactly what this dual is, but that can be clarified by removing the original fullerene. What’s left is called a geodesic sphere — or, quite informally, a ball made of many triangles. The larger a fullerene is, the more hexagonal rings/faces it will have, and the more triangles will be found on the geodesic sphere which is its dual. For the 240-atom fullerene shown repeatedly, above, here is the dual, by itself, with different colors indicating slightly different triangle-shapes. (An exception is the yellow and green triangles, which are congruent, but have different colors for aesthetic reasons.)
I made these four rotating images using Stella 4d: Polyhedron Navigator. To try this program for yourself, simply visit www.software3d.com/Stella.php. At that site, there is a free trial download available.
The Sun, in a Cloudless Sky
The Rhombic Hexacontahedron
The rhombic hexacontahedron (sometimes spelled “hexecontahedron”) is one of many stellations of the rhombic triacontahedron. Its sixty faces, like the thirty faces of the rhombic triacontahedron, are golden rhombi — rhombi with diagonals in the golden ratio.
The rotating image above was produced using Stella 4d: Polyhedron Navigator, a program available at www.software3d.com/Stella.php.
On “Digging to China”
When I was a little kid, my sister and I dug a big hole, in our front yard, and simply called it “the digging-hole.” It looked a lot like the hole shown above, except for the fact that, during daylight hours, our digging-hole usually included two small, dirt-covered, determined children, armed with plastic shovels. We tried, for years, to dig that hole as deep as possible. My personal goal, of course, was the Earth’s molten core, not India, and certainly not China.
Why do Americans so often talk about digging a hole straight down to China, anyway? Even if the Earth were solid all the way through its interior, digging straight down, from almost anywhere in the contiguous 48 states of the USA, would not put you in China, nor even India (which is, at least, closer to being correct than is China), but at the bottom of the Southern Indian Ocean. Salty water would suddenly rush into your newly-dug tunnel, killing you instantly, as soon as you got close to enough to the other side for the extreme water-pressure there to finish your digging project for you. The only exceptions to this watery doom would be coming out of the tunnel on one of the islands in that ocean, which would require great precision to hit deliberately.
Also, the fact that China and the USA are both Northern-hemisphere nations easily rules China out as the hypothetical “solid-earth” destination for Americans who dig straight down, and all the way through. If you could go through the center of the earth from North of the equator, you’d have to end up South of the equator. Isn’t that obvious? Don’t people look at globes?
One of Many Possible Facetings of the Rhombicosidodecahedron
I created this using Stella 4d: Polyhedron Navigator, available at www.software3d.com/Stella.php. Faceting involves connecting different sets of vertices (relative to the original polyhedron) to form new edges and faces. The new edges and faces, both, typically intersect each other, although often not as many times as in this particular example of a faceted polyhedron.
“Evolution is just a theory.” Please STOP saying this!
Why?
Well, just to get started, these three things are also “just” theories:
1. Germs are the cause of many diseases.
2. Everything you have ever touched is made of atoms.
3. The spinning earth doesn’t fling us into outer space because of gravity.
Would any reasonable person actually think the phrase “just a theory” makes sense for any of these three things? Use of this phrase, for evolution, the Big Bang, or anything else, indicates one thing: the person talking does not understand the meaning of the word “theory.” Theories are the best science has to offer, and science is the foundation of modern civilization. These theories are based on the repeated testing of hypotheses, using experiment, to explain what we observe — so they are evidence-based explanations, not mere guesses, as the annoying phrase “just a theory” implies.
Evolution is every bit as well-established a theory as the three examples cited above. All theories are subject to further testing, which is an important self-correcting mechanism in science. No theory is beyond revision or replacement, if new experimental evidence calls for it. However, that fact doesn’t make any particular theory invalid — it simply helps explain why science works. It also works just as well whether people believe in it, or approve of it, or agree with it — or not.
If you want to disprove the theory of evolution, just find a fossilized rabbit in a one-billion-year-old rock, as J.M.S. Haldane famously observed. It will only take one such finding to accomplish your goal, and you can publish your results, and become famous – if you can find such a fossil. For your own safety, though, please do not hold your breath while looking.
A Quote from Voltaire, on Absurdities and Atrocities
Examples abound. Here are two:
Absurdity #1: Pure human races exist.
A resulting atrocity: the Holocaust (~20 million people, including ~6 million Jews, killed by the Nazis in the 1930s and 1940s).
Absurdity #2: Acts which are both suicidal and homicidal can be wonderful things, and can earn a person an eternal reward in paradise after death.
A resulting atrocity: the destruction of the World Trade Center, and attacks on other targets, on September 11, 2001, which killed over three thousand people, including the hijackers themselves.
Please note that this list is far from complete. A complete list would fill several very large books. Beware of absurdities in your thinking, for they can actually be fatal.