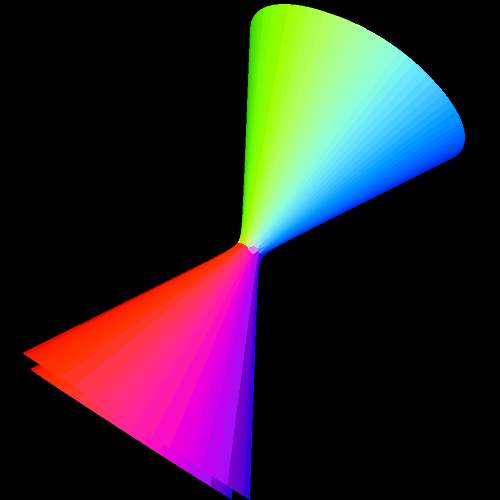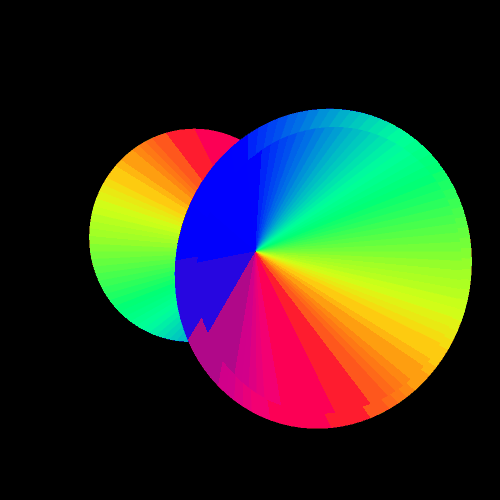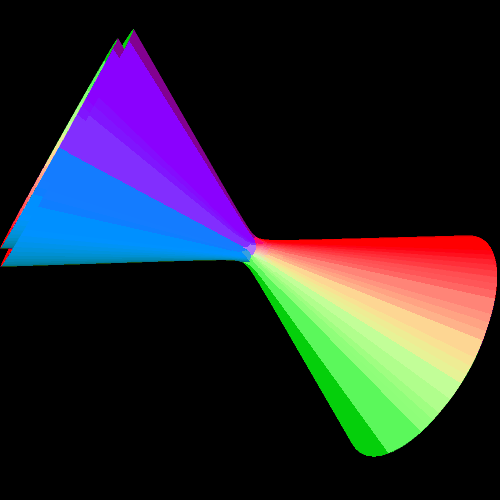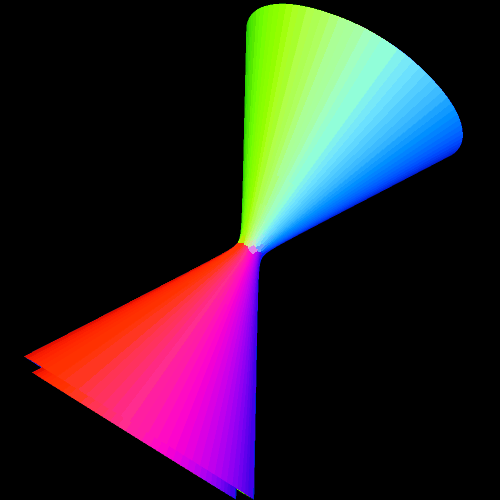Five Faceted Polyhedra

Posted on 17 February 2016 by RobertLovesPi

Above, on the left, is a faceted cuboctahedron. To its right are a faceted snub dodecahedron (upper right) which is also a ten-part compound, and a faceted truncated cube below that. Any of these images may be enlarged by clicking on it.

Below, the left figure is a faceting of the great rhombcuboctahedron — one which is also a three-part compound of octagonal prisms. To its right is a faceting of the snub dodecahedron which is markedly different in appearance from the snub dodecahedron faceting shown above.

Faceted polyhedra have the same vertices as the polyhedra from which they are derived, but those vertices are connected in different ways, changing the faces and edges.

All of these were made using Stella 4d, a program you may try for yourself, for free, right here.

A Pyritohedral and Pentagon-Faced Polyhedron

Posted on 17 February 2016 by RobertLovesPi

pyritohedral 36 pentagons

Twelve of the faces of this polyhedron are pink, and the other twenty-four are blue. It has no faces which are not pentagons. I made it using Stella 4d: Polyhedron Navigator, which is avialable at http://www.software3d.com/Stella.php.

Polyhedral Peacock

Posted on 16 February 2016 by RobertLovesPi

peacock

Created using Stella 4d, available at http://www.software3d.com/Stella.php.

A Logic Problem Involving Marvel Super-Heroes

Posted on 13 February 2016 by RobertLovesPi

Movies_Spider_man_Spider_man_DareDevil_Iron_Man_Captain_America_Wolverine_Black_43340_detail_thumb

Iron Man, Daredevil, Spider-Man, Captain America, and Wolverine each have a favorite food, a favorite beverage, own one pet, and have a single hobby. Based on the clues which follow, find out these things:

Which hero’s favorite food is (A) pizza, (B) green eggs and ham, (C) apple pie, (D) Chinese take-out, and (E) caviar?
Which hero’s favorite beverage is (A) beer, (B) vodka, (C) Coca-Cola, (D) water, and (E) chocolate milkshakes?
Which hero owns (A) a black cat, (B) a porcupine, (C) a robot dog, (D) an iguana, and (E) a real dog?
Which hero’s hobby is (A) coin collecting, (B) stamp collecting, (C) collecting comic books, (D) collecting seashells, and (E) collecting rocks?

Here are the clues. Answers will be revealed in the comments, but only after someone solves the puzzle (to avoid spoiling anyone’s fun).

Wolverine drinks beer.
Daredevil is blind. The other four heroes can all see.
Spider-Man eats pizza.
Wolverine has a mutant healing factor that allows him to rapidly heal from injuries.
Iron Man is the only one of these five heroes who wears a suit of armor.
The hero whose favorite food is apple pie always eats it with his favorite drink, Coca-Cola.
Iron Man drinks vodka.
All of the heroes who can see refuse to eat green eggs and ham.
Of these five heroes, no one without either a mutant healing factor or a suit of armor would be dumb enough to keep a porcupine as a pet.
Iron Man, an accomplished inventor, refuses to own a pet which he did not build himself.
The hero who eats apple pie doesn’t like chocolate, nor chocolate-flavored anything.
Iron Man has more money than all the other heroes combined.
The hero whose favorite food is pizza does not own a dog.
The seashell-collector is blind.
The owner of a real dog also collects stamps.
The porcupine-owner doesn’t like apple pie.
Spider-Man likes the black cat, but has to visit the cat’s owner in order to see her.
The richest hero eats caviar.
The coin collector doesn’t like pizza, nor porcupines.
The comic-book collector hates drinking water. He also doesn’t like milkshakes of any kind.
The owner of the black cat is lactose-intolerant, and, for this reason, doesn’t drink milkshakes.

The first person to leave the solutions in the comments wins bragging rights.

[Source of image: http://www.hdwallpaperpc.com/show-wallpaper/Spider_man_DareDevil_Iron_Man_Captain_America_Wolverine_Black_43340.html].

Unsquashing the Squashed Meta-Great-Rhombcuboctahedron

Posted on 12 February 2016 by RobertLovesPi

I noticed that I could arrange eight great rhombcuboctahedra into a ring, but that ring, rather than being regular, resembled an ellipse.

I then made a ring of four of these elliptical rings.

After that, I added a few more great rhombcuboctahedra to make a meta-rhombcuboctahedron — that is, a great rhombcuboctahedron made of rhombcuboctahedra. However, it’s squashed. (I believe the official term for this is “oblate,” but “squashed” also works, at least for me.)

So now I’m wondering if I can make this more regular. In other words, can I “unsquash” it? I notice that even this squashed metapolyhedron has regular rings on two opposite sides, so I make such a ring, and start anew.

I then make a ring of those . . .

. . . And, with two more ring-additions, I complete the now-unsquashed meta-great-rhombcuboctahedron. Success!

To celebrate my victory, I make one more picture, in “rainbow color mode.”

[All images made using Stella 4d, available here: http://www.software3d.com/Stella.php.]

A Torus and Its Dual, Part II

Posted on 12 February 2016 by RobertLovesPi

After I published the last post, which I did not originally intend to have two parts, this comment was left by one of my blog’s followers. My answer is also shown.

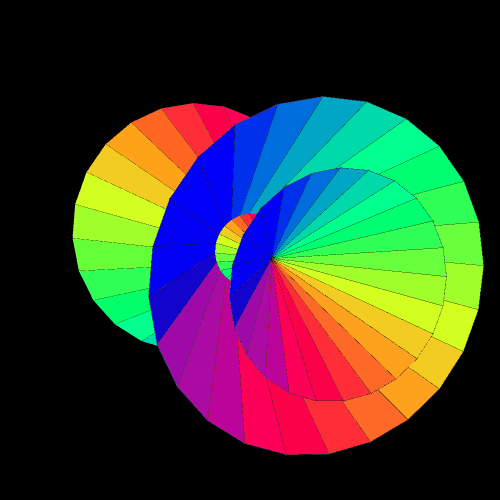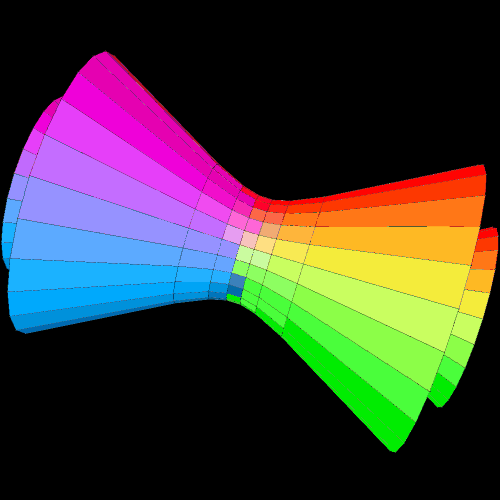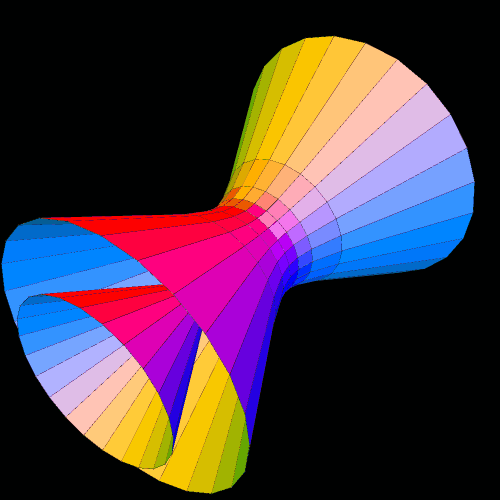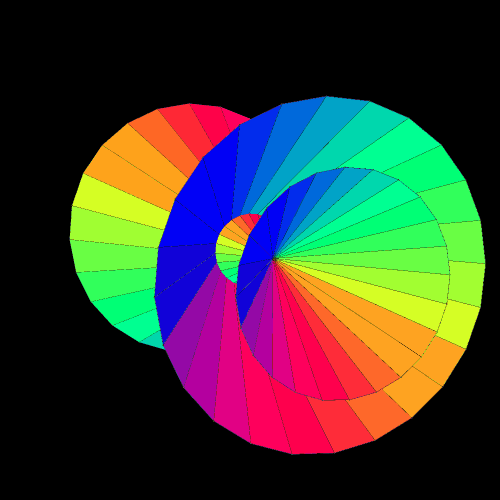
A torus can be viewed as a flexible rectangle rolled into a donut shape, and I had used 24 small rectangles by 24 small rectangles as the settings for Stella 4 for the torus, and its dual, in the last post — which, due to the nature of that program, are actually rendered as toroidal polyhedra. To investigate my new question, I increased 24×24 to 90×90, and these three images show the results. The first shows a 90×90 torus, the second shows its dual, and the third shows the compound of the two.

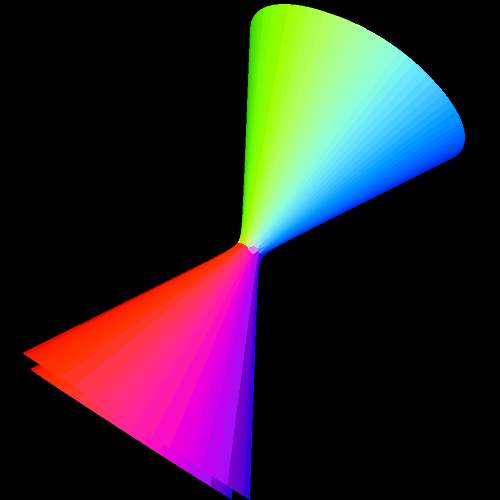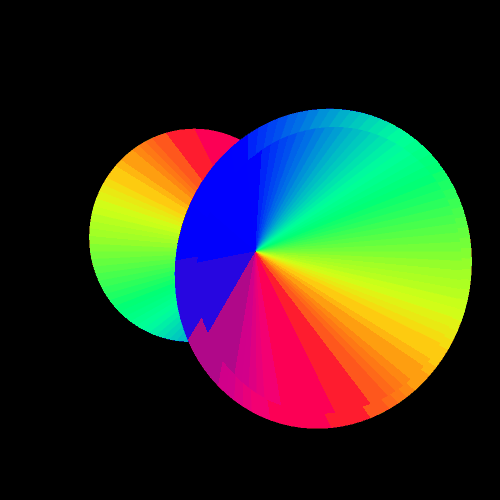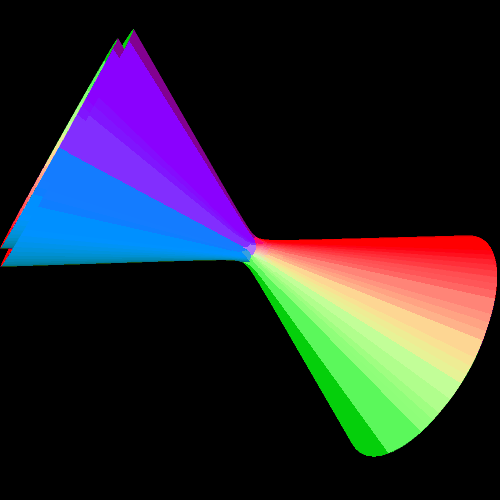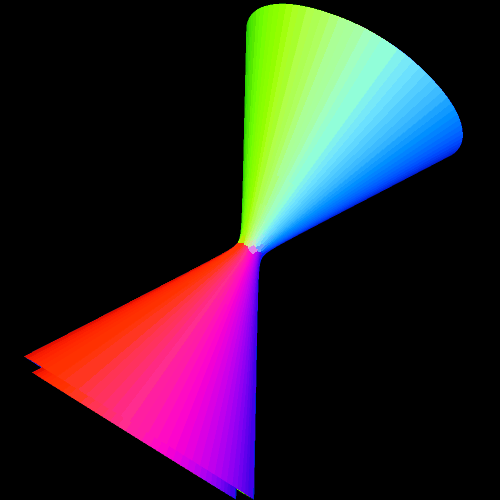
When I compare these images to those in the previous post, it is clear that these figures are approaching a limit as n, in the expression “nxn rectangle,” increases. What’s more, I recognize the dual now, of the true torus, at the limit, as n approaches infinity — it’s a cone. It’s not a finite-volume cone, but the infinite-volume cone one obtains by rotating a line around an axis which intersects that line. This figure, not a finite-volume cone, is the cone used to define the conic sections: the circle, ellipse, parabola, and hyperbola.

What’s more, I smell calculus afoot here. I do not yet know enough calculus.

“Learn a lot more about calculus” is definitely on my agenda for the coming Summer, for several reasons, not the least of which is that I plainly need it to make more headway in my understanding of geometry.

[Note: Stella 4d, the program used to make these images, may be found at http://www.software3d.com/Stella.php.]

A Torus and Its Dual, Part I

Posted on 12 February 2016 by RobertLovesPi

The torus is a familiar figure to many, so I chose a quick rotational period (5 seconds) for it. The dual of a torus — and I don’t know what else to call it — is not as familiar, so, for it, I extended the rotational period to 12 seconds.

By viewing the compound of the torus and its dual, one can see the the dual is the larger of the two, by far:

I used Stella 4d to make these images. It’s a program you can buy, or try for free, at this website: http://www.software3d.com/Stella.php.

My Possible Encounter with Ron Paul

Posted on 11 February 2016 by RobertLovesPi

So, while driving on an Arkansas highway, I had an encounter with Ron Paul.

Maybe.

What I know with certainty is that I saw a vehicle with a license plate that stated, “RONPAUL.”

I was unable to catch up with this vehicle to check to see if it was being driven by, um, the Ron Paul, and this is due to Ron Paul’s/the driver’s libertarian principles.

And, by “libertarian principles,” I mean that this guy, whoever he was, was driving just as fast as he wanted to.

# # #

[Photo from Ron Paul’s Wikipedia page.]

Ten Commandments of the Universe, Set to Music

Posted on 9 February 2016 by RobertLovesPi

IDL TIFF file

Because there’s nothing wrong with mixing a little Rolling Stones with your physics, that’s why.

Beginning the Fractiles-7 Refrigerator Experiment

Posted on 7 February 2016 by RobertLovesPi

To begin this experiment, I first purchased two refrigerator-sized Fractiles-7 sets (available at http://fractiles.com/), and then, early on a Sunday, quietly arranged these rhombus-shaped magnets on the refrigerator in our apartment (population: 4, which includes two math teachers and two teenagers), using a very simple pattern.

160207_0000

Here’s a close-up of the center. There are 32 each, of three types of rhombus., in this double-set, for a total of 96 rhombic magnets, all with the same edge length.

160207_0001

The number of possible arrangements of these rhombi is far greater than the population of Earth.

The next step of the experiment is simple. I wait, and see what happens.

It should be noted that there is a limit on how long I can wait before my inner mathematical drives compel me to play with these magnets more, myself — but I do not yet know the extent of that limit.