
In this polyhedron, half the faces are the two dozen light-blue kites, and the other half are isosceles triangles. I made it using Stella 4d, software you can buy, or try for free, at this website.

In this polyhedron, half the faces are the two dozen light-blue kites, and the other half are isosceles triangles. I made it using Stella 4d, software you can buy, or try for free, at this website.
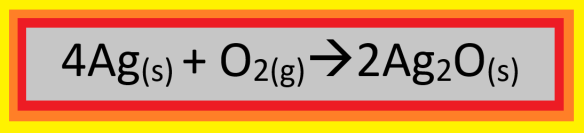
Because of the price of silver being literally on fire, they will not be buying and selling troy ounces of metallic silver when the markets open in New York tomorrow morning. Instead, they will be selling “oxide ounces” of silver oxide, in sealed-plastic capsules of this black powder, with an oxide ounce of silver oxide being defined as that amount of silver oxide which contains one troy ounce of silver.

A troy ounce of silver is 31.1 grams of that element, which has a molar mass of 107.868 g/mole. Therefore, a troy ounce of silver contains (31.1 g)(1 mol/107.868 g) = 0.288 moles of silver. An oxide ounce of silver oxide would also contain oxygen, of course, and the formula on the front side of a silver oxide capsule (shown above; information on the back of the capsule gives the number of oxide ounces, which can vary from one capsule to another) is all that is needed to know that the number of moles of oxygen atoms (not molecules) is half the number of moles of silver, or (0.288 mol)/2 = 0.144 moles of oxygen atoms. Oxygen’s non-molecular molar mass is 15.9994 g, so this is (0.144 mol)(15.9994 g/mol) = 2.30 g of oxygen. Add that to the 31.1 g of silver in an oxide ounce of silver oxide, and you have 31.1 g + 2.30 g = 33.4 grams of silver oxide in an oxide ounce of that compound.
In practice, however, silver oxide (a black powder) is much less human-friendly than metallic silver bars, coins, or rounds. As you can easily verify for yourself using Google, silver oxide powder can, and has, caused health problems in humans, especially when inhaled. This is the reason for encapsulation in plastic, and the plastic, for health reasons, must be far more substantial than a mere plastic bag. For encapsulated silver oxide, the new industry standard will be to use exactly 6.6 g of hard plastic per oxide ounce of silver oxide, and this standard will be maintained when they begin manufacturing bars, rounds, and coins of silver oxide powder enclosed in hard plastic. This has created a new unit of measure — the “encapsulated ounce” — which is the total mass of one oxide ounce of silver oxide, plus the hard plastic surrounding it on all sides, for a total of 33.4 g + 6.6 g = 40.0 grams, which will certainly be a convenient number to use, compared to its predecessor-units.
# # #
[This is not from The Onion. We promise. It is, rather, a production of the Committee to Give Up on Getting People to Ever Understand the Meaning of the Word “Literally,” or CGUGPEUMWL, which is fun to try to pronounce.]

Source: Soon to be a Major Motion Picture, p. 214.

I used three things to make this: Geometer’s Sketchpad (to make one black and white version; the whole thing is made of semicircles), MS-Paint (to color the six different versions which appear here), and the website http://www.makeagif.com (to assemble the six separate still images into one .gif file, with the illusion of motion). The surprising thing to me was how fast the process was, once I had the idea of my goal for a finished product.

Many Americans are experiencing the same dilemma right now — we’re trying to decide whether to vote against Donald Trump for president (by casting a vote “for” Hillary Clinton), or vote against Hillary Clinton (by casting a vote “for” Trump). Voters who actually want to vote for either of the major-party candidates are much rarer, this time, than is typically the case, as recent news stories have documented.
I’ve said for months that I would vote against Trump (again — for I already voted against him once, by voting in my state’s G.O.P. primary election). As November gets closer, though, I am finding the idea of voting against Trump in November, by holding my nose, and casting a vote for Clinton, to be a progressively less palatable idea. I like to have both hands free when I vote, you see, so I’d need to use a clothespin, for my nose, to actually do this. The problem is, of course, that I’m far from alone with my opinions about this election — and I’m not sure exactly how many clothespins we have in the USA. There might actually not be enough for all the “against” votes people intend to cast.
In the face of this potentially-devastating, nationwide clothespin shortage, I finally decided to do something else: look for someone I can actually vote for, in good conscience, without fear of being horribly embarrassed by my vote within days of our new president taking the oath of office.
I didn’t find one such person. I actually found two. (Image source: here.)

I’m not a Libertarian, nor am I a member of the Green Party. Having examined both of these candidates, though, I find that I agree with each of them on many things, and disagree with them on a smaller number of issues. The major thing they have in common is also their major political “selling point” in this election — not being Trump, nor Clinton.
Once I make a decision between Gary Johnson and Jill Stein, I will have accomplished two things which are important to me: (1) finding someone to actually vote for, rather than casting a 100% “against” vote, and (2) finding a way to vote against the two major-party candidates — both of them — at the same time.
While comments on this post are welcome, please don’t simply point out to me that either Hillary Clinton or Donald Trump will almost certainly win the election in November. This is something I already know, and it does not affect my decision. Either of them could win in November . . . but neither of them will get any help from me to do so.

Mathematicians have discovered more than one set of rules for polyhedral stellation. The software I use for rapidly manipulating polyhedra (Stella 4d, available here, including as a free trial download) lets the user choose between different sets of stellation criteria, but I generally favor what are called the “fully supported” stellation rules.
For this exercise, I still used the fully supported stellation rules, but set Stella to view these polyhedra as having only tetrahedral symmetry, rather than icosidodecahedral (or “icosahedral”) symmetry. For the icosahedron, this tetrahedral symmetry can be seen in this coloring-pattern.
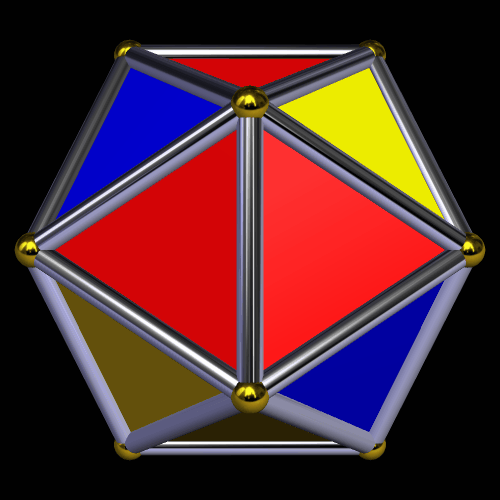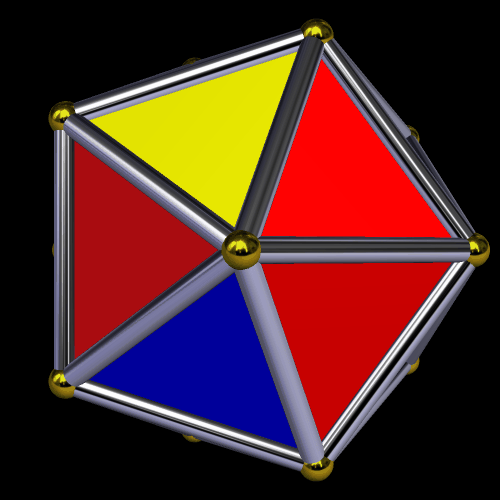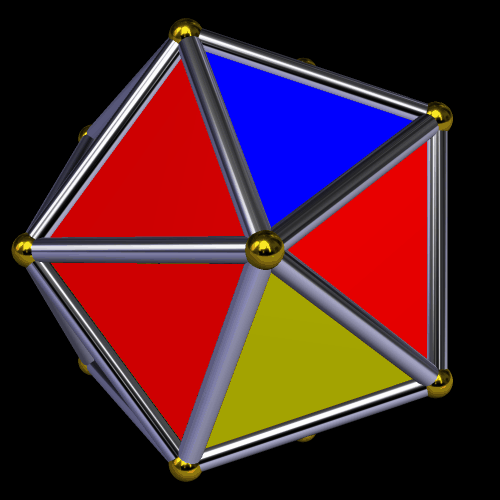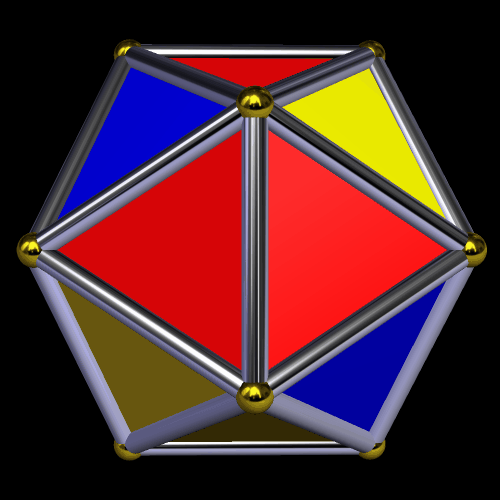
The next image shows what the icosahedron looks like after a single stellation, when performed through the “lens” of tetrahedral symmetry. This stellation extends the red triangles as kites, and hides the yellow triangles from view in the process.
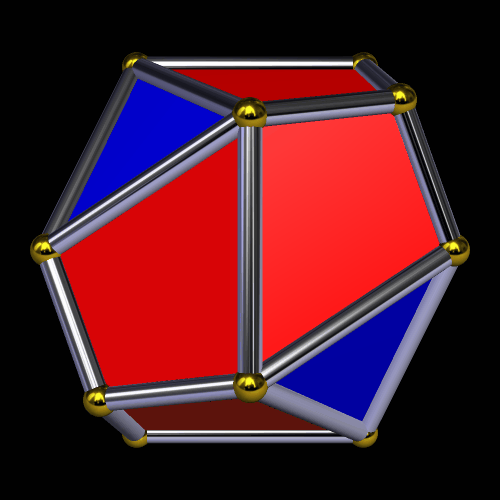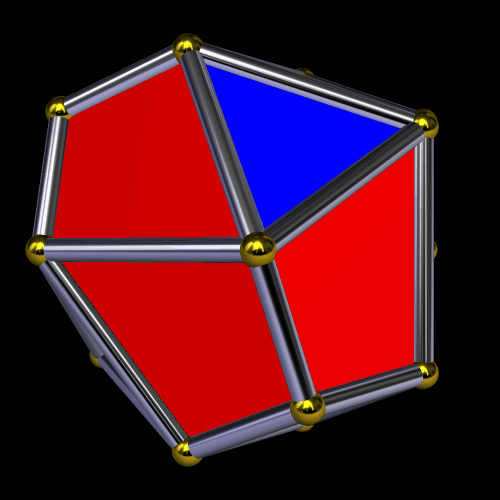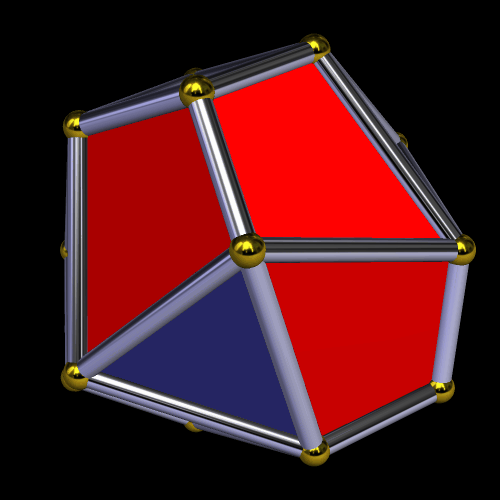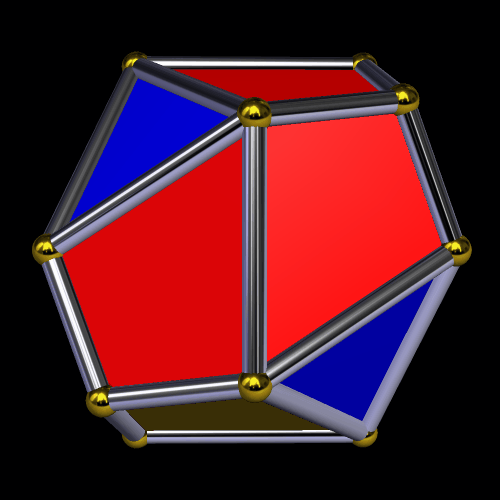
The second such stellation produces this polyhedron — a pyritohedral dodecahedron — by further-extending the red faces, and obscuring the blue triangles in the process.

The third tetrahedral stellation of the icosahedron produces another pyritohedral figure, which further demonstrates that pyritohedral symmetry is related to both icosidodecahedral and tetrahedral symmetry.

The fourth such stellation produces a Platonic octahedron, but one where the coloring-scheme makes it plain that Stella is still viewing this figure as having tetrahedral symmetry. Given that the octahedron itself has cuboctahedral (or “octahedral”) symmetry, this is an increase in the number of polyhedral symmetry-types which have appeared, so far, in this brief survey.

Next, I looked at the fifth tetrahedral stellation of the icosahedron, and was surprised at what I found.

While I was curious about what would happen if I continued stellating this polyhedron, I also wanted to see this fifth stellation’s convex hull, since I could already tell it would have only hexagons and triangles as faces. Here is that convex hull:

For the last step in this survey, I performed one more tetrahedral stellation, this time on the convex hull I had just produced.
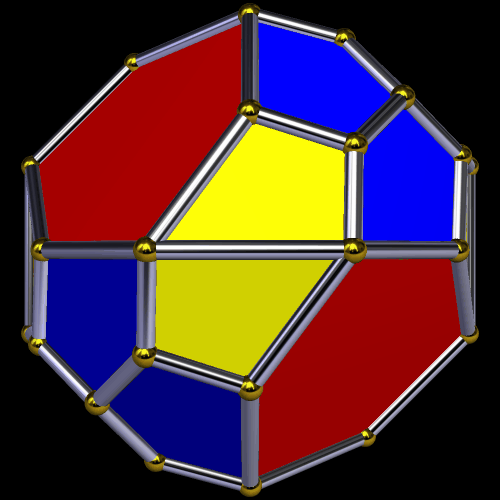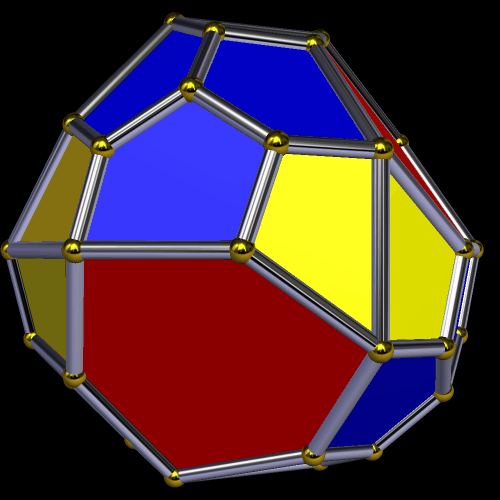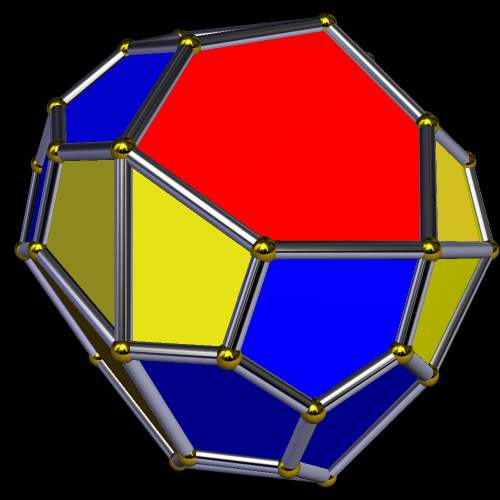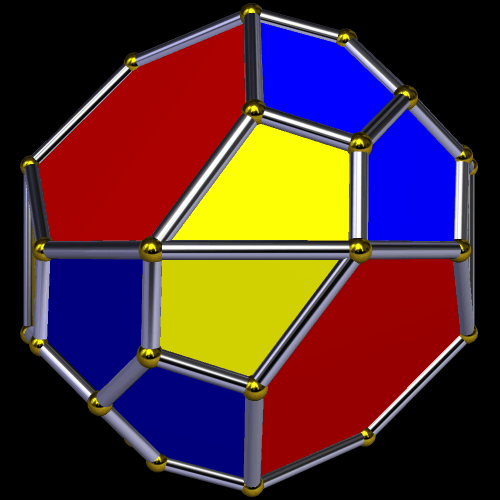

To make the first of these variations, above, I augmented each triangular face of a snub dodecahedron with an antiprism 2.618 times as tall as the triangles’ edge length, and then took the convex hull of the result. The other polyhedra shown, below, were obtained by various other manipulations of the snub dodecahedron, all performed using a program called Stella 4d: Polyhedron Navigator, which you can try right here.

The variant above looked like it needed a name, so I called it an expanded snub truncated dodecahedron. As for the one below, it is one of many facetings of the snub dodecahedron.

Finally, the last figure shown (stumbled upon during a “random walk” with Stella) is one of many possible figures which are non-convex relatives of the snub dodecahedron.

It’s a mystery to me why this happens, but the parallels between different conversations which start with this question are simply amazing. First, I don’t get asked this question unless talking to a teenager . . . and then, nearly every time this happens, the rest of the conversation follows the same pattern.
First, I answer the question honestly, with a single word, by simply naming my favorite color.

After telling this one-word, five-letter truth, I then get a response which has become utterly predictable: “Black’s not a color!”
Even stranger: such inquisitions only seem to come from teenagers who are dressed in such a way as to let the following response work: “What color is your t-shirt?”
Sometimes they even look down at that point, presumably to check, which lets them see the answer to my question for themselves:

After that one question from me, for some reason, they tend not to say much more.

Although this was based on something I constructed using the Fractiles-7 magnetic tiling toy, I did not have enough magnetic pieces to finish this. The idea was, therefore, converted into a (non-Euclidean) construction using Geometer’s Sketchpad, and then refined using MS-Paint. The reason I describe this as a non-Euclidean construction is that an angle of pi/7 radians, such as the acute angles in the red rhombi, cannot be constructed using compass and unmarked straight edge: antiquity’s Euclidean tools. The other angles used are whole-number multiples of pi/7 radians, up to and including 6pi/7 radians for the obtuse angles of the red rhombi.
The yellow rhombi have angles measuring 2pi/7 and 5pi/7 radians, while the blue rhombi’s angles measures 3pi/7 and 4pi/7 radians. None of these angles have degree measures which are whole numbers. It is no coincidence that 7 is not found among the numerous factors of 360. It is, in fact, the smallest whole number for which this is true.
I have a conjecture that this aperiodic radial tiling-pattern could be continued, using these same three rhombi, indefinitely, but this has not yet been tested beyond the point shown.