As if the world needed another trigonometric function, I give it the WM function, named after the letters apparent in its graph. It is the sine of the sine of x, times 2π, if x is measured in radians, as in the graph below.
Author Archives: RobertLovesPi
Trigonometric Stained-Glass Windows
To make the virtual “painting” above, I plotted simple and moderately-complex trigonometric functions on a single coordinate plane, as shown below, using Geometer’s Sketchpad. I then erased all the text, etc., copied-and-pasted a screenshot into MS-Paint, and used that program to make the finished image above.
A Rhombic Enneacontahedron, Augmented with Sixty Rhombic Dodecahedra, Along with Its Dual
The dual to this cluster-polyhedron appears below. Both virtual models were created using Stella 4d: Polyhedron Navigator, software available here.
Octagons, Hexagons, and Squares
Hexagons and Octagons
A Tessellation Featuring Multicolored, Regular Tetracontagons, as Well as Tetraconcave, Black, and Equilateral Hexatriacontagons
A Kite-Faced Polyhedron Based on the Cube, Octahedron, and Rhombic Dodecahedron
Above is the entire figure, showing all three set of kites. The yellow set below, though, lie along the edges of a rhombic dodecahedron.
The next set, the blue kites, lie along the edges of an octahedron.
Finally, the red set of kites lies along the edges of a cube — the dual to the octahedron delineated by the blue kites.
These images were made using Stella 4d, which is available here.
“Fractured” Octahedra
These are variations of the octahedron. I made them all with Stella 4d, which is available here. “Fractured” isn’t an official term, as “truncated or stellated” are, but I can’t come up with a better description, at least not yet. Other suggestions are welcome.
A Variant of the Octahedron Which Features Regular Dodecagons and Quadrilaterals of Three Types
(See here for more information on Stella 4d, the software used to create this image.)
Six Hexagons and Four Triangles, As Faces of a Small Polyhedron
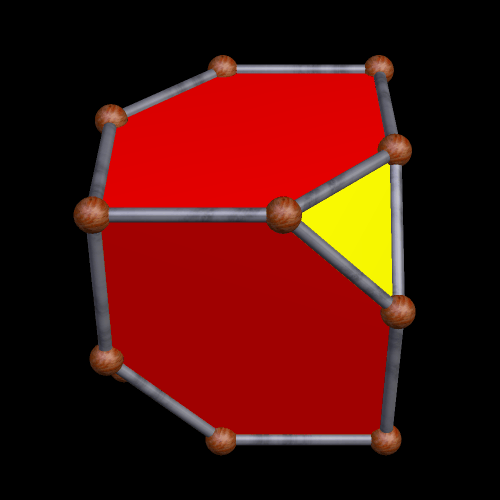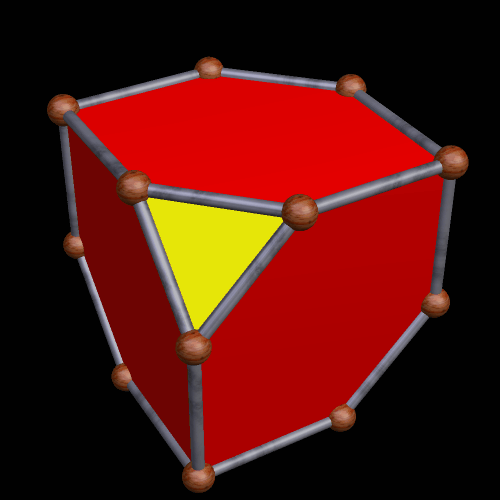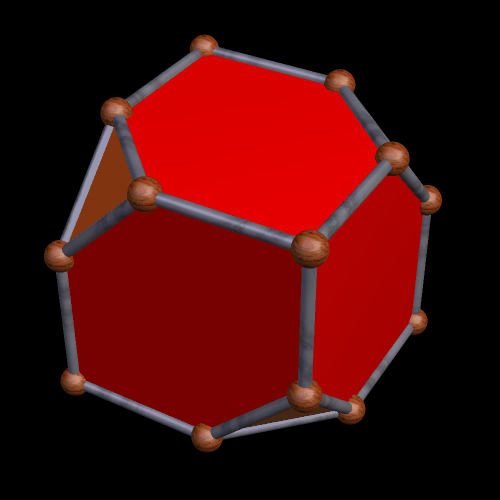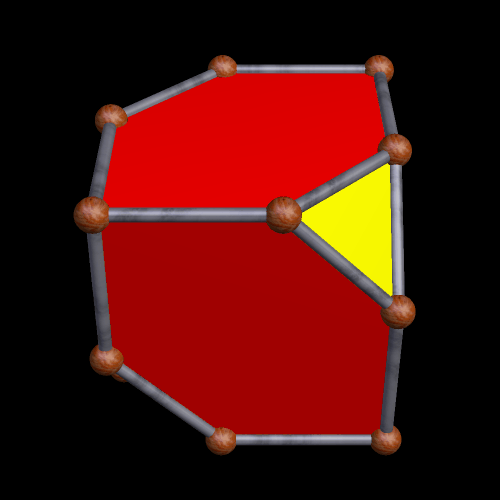
One could call this a half-truncated cube. A fully truncated cube has eight triangular faces, created by truncation, and this has half as many.
(See here for more information on Stella 4d, the software used to create this image.)