This is one of many possible facetings of the truncated icosahedron. I made it using Stella 4d, which you can try for yourself at this website: http://www.software3d.com/Stella.php.
A Faceted Truncated Icosahedron
Reply
Tag Archives: faceted
A Faceting of the Rhombcuboctahedron
This particular faceting of the rhombcuboctahedron can also be viewed as a cluster of stella octangulae. I made it using Stella 4d, polyhedron-manipulating software you can try, for yourself, at http://www.software3d.com/Stella.php.
A Faceted Great Rhombcuboctahedron
Some prefer to call the great rhombcuboctahedron the “truncated cuboctahedron,” instead. Whichever term you prefer, this is a faceted version of that Archimedean solid. I made it using Stella 4d: Polyhedron Navigator, software you may find here.
A Hollow Faceting of the Rhombicosidodecahedron, and Its Hollow Dual
The images above all show a particular faceting of the rhombicosidodecahedron which, to my surprise, is hollow. It has the vertices of a rhombicosidodecahedron, but two different face-types, as seen in the smaller pictures: yellow hexagons, and red isosceles trapezoids. (To enlarge any image in this post, simply click on it.)
The dual of this polyhedron is even more obviously hollow, as seen below. Its faces, as seen in the still picture, are crossed hexagons — with edges which cross three times per hexagon, no less.
The software I used to make these polyhedra, Stella 4d, will return an error message if the user attempts to make a polyhedron which is not mathematically valid. When I’ve made things that look (superficially) like this before, I used “hide selected faces” to produce hollow geometrical figures which were not valid polyhedra, but that isn’t what happened here (I hid nothing), so this has me confused. Stella 4d (software you can buy, or try for free, here) apparently considers these valid polyhedra, but I am at a loss to explain such familiar concepts as volume for such unusual polyhedra, or how such things could even exist — yet here they are. Clarifying comments would be most appreciated.
Standard and Faceted Versions, Side by Side, of Each of the Thirteen Archimedean Solids
These two polyhedra are the truncated tetrahedron on the left, plus at least one faceted version of that same Archimedean solid on the right. As you can see, in each case, the figures have the same set of vertices — but those vertices are connected in a different way in the two solids, giving the polyhedra different faces and edges.
(To see larger images of any picture in this post, simply click on it.)
The next three are the truncated cube, along with two different faceted truncated cubes on the right. The one at the top right was the first one I made — and then, after noticing its chirality, I made the other one, which is the compound of the first faceted truncated cube, plus its mirror-image. Some facetings of non-chiral polyhedra are themselves non-chiral, but, as you can see, chiral facetings of non-chiral polyhedra are also possible.
The next two images show a truncated octahedron, along with a faceted truncated octahedron. As these images show, sometimes faceted polyhedra are also interesting polyhedra compounds, such as this compound of three cuboids.
The next polyhedra shown are a truncated dodecahedron, and a faceted truncated dodecahedron. Although faceted polyhedra do not have to be absurdly complex, this pair demonstrates that they certainly can be.
Next are the truncated icosahedron, along with one of its many facetings — and with this one (below, on the right) considerably less complex than the faceted polyhedron shown immediately above.
The next two shown are the cuboctahedron, along with one of its facetings, each face of which is a congruent isosceles triangle. This faceted polyhedron is also a compound — of six irregular triangular pyramids, each of a different color.
The next pair are the standard version, and a faceted version, of the rhombcuboctahedron, also known as the rhombicuboctahedron.
The great rhombcuboctahedron, along with one of its numerous possible facetings, comes next. This polyhedron is also called the great rhombicuboctahedron, as well as the truncated cuboctahedron.
The next pair are the snub cube, one of two Archimedean solids which is chiral, and one of its facetings, which “inherited” its chirality from the original.
The icosidodecahedron, and one of its facetings, are next.
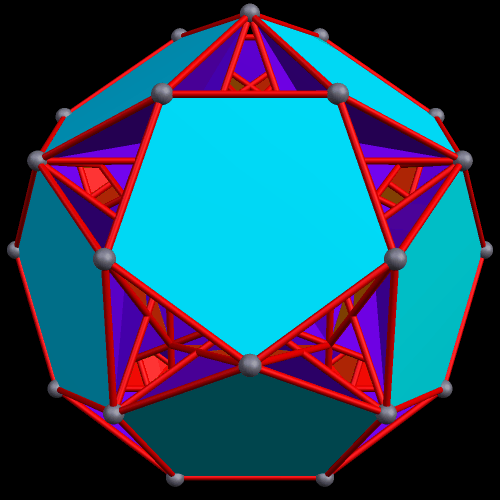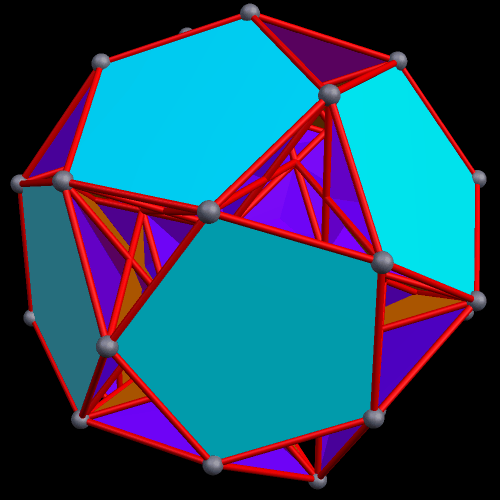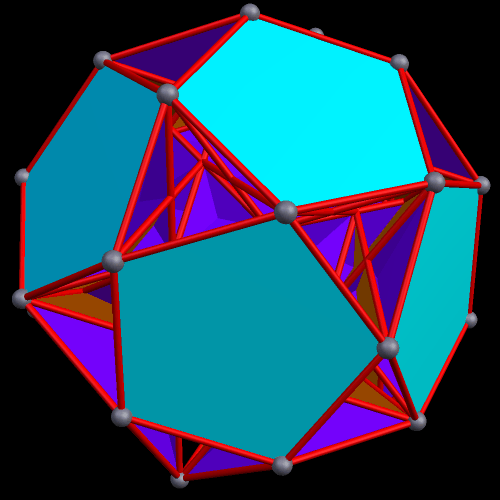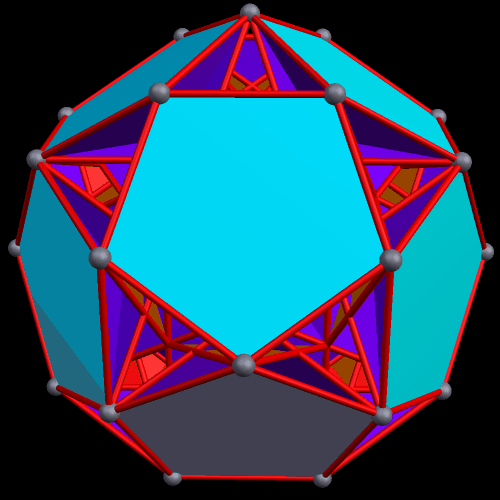
The next pair are the original, and one of the faceted versions, of the rhombicosidodecahedron.
The next two are the great rhombicosidodecahedron, and one of its facetings. This polyhedron is also called the truncated icosidodecahedron.
Finally, here are the snub dodecahedron (the second chiral Archimedean solid, and the only other one, other than the snub cube, which possesses chirality), along with one of the many facetings of that solid. This faceting is also chiral, as are all snub dodecahedron (and snub cube) facetings.
Each of these polyhedral images was created using Stella 4d: Polyhedron Navigator, software available at this website.
Five Faceted Polyhedra
Above, on the left, is a faceted cuboctahedron. To its right are a faceted snub dodecahedron (upper right) which is also a ten-part compound, and a faceted truncated cube below that. Any of these images may be enlarged by clicking on it.
Below, the left figure is a faceting of the great rhombcuboctahedron — one which is also a three-part compound of octagonal prisms. To its right is a faceting of the snub dodecahedron which is markedly different in appearance from the snub dodecahedron faceting shown above.
Faceted polyhedra have the same vertices as the polyhedra from which they are derived, but those vertices are connected in different ways, changing the faces and edges.
All of these were made using Stella 4d, a program you may try for yourself, for free, right here.
Multiple Facetings of the Icosidodecahedron
To create a faceted icosidodecahedron, you simply start with an icosidodecahedron, then remove its edges and faces. Next, you connect the vertices differently, thus creating new faces and edges. As you can see below, this can be done in many different ways.
All these were created using Stella 4d, software you may try for free at http://www.software3d.com/Stella.php.
A Faceted Icosidodecahedron with 48 Faces
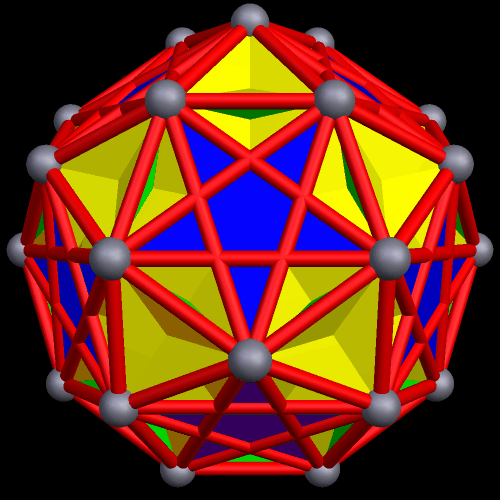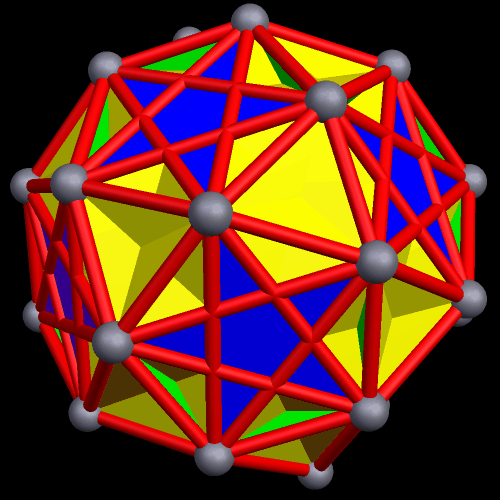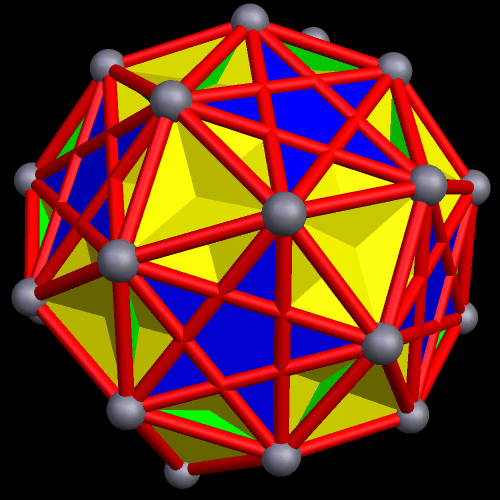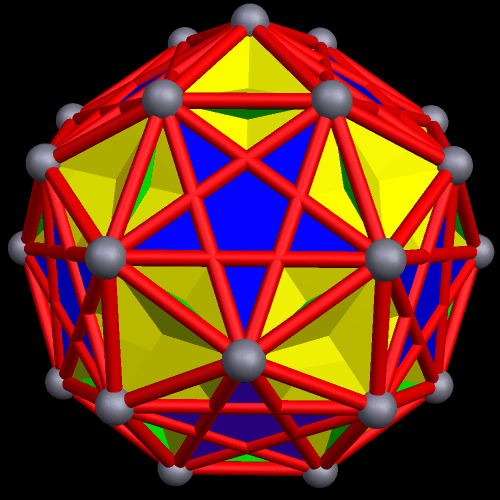
The 48 faces of this faceted icosidodecahedron are:
- 6 green regular decagons (difficult to see, because they pass through the figure’s center)
- 30 golden rectangles, shown in yellow, and each interpenetrating other faces
- 12 blue star pentagons
Software called Stella 4d was used to make this, and it is available (with a free trial download available) at this website.
A Compound of Ten Elongated Octahedra Which Is Also a Particular Faceting of the Rhombicosidodecahedron, Together with Its Dual
Thinking about the post immediately before this one led me to see if I could connect opposite triangular faces of a rhombicosidodecahedron to form a ten-part compound — and it worked with Stella 4d just as it had when I “previewed” it in my head.
The interesting dual of the above polyhedral compound, also a ten-part compound, I was not able to preview in my head (although that would be a nice ability to have), but creating it was easy with Stella:
It is difficult, in the dual, to tell what the ten components are. To help with this, in the next image, all but one component has been removed. This reveals the components of the dual to be rhombus-faced parallelopipeds which are quite flattened, compared to most parallelopipeds I have seen before. This polyhedron is isomorphic to the cube, just as the elongated octahedra in the first compound were each isomorphic to the Platonic octahedron. Given that the cube and octahedron are duals, this is no surprise.
Stella 4d may be tried for free, as a trial download, at this website: http://www.software3d.com/Stella.php.
A Compound of Fifteen Cuboids — Which Is Also a Particular Faceting of the Icosidodecahedron
The creator of Stella 4d, the program I used to make these rotating polyhedral images, is Robert Webb (and the software itself may be tried for free here). Recently, on Facebook, he displayed a paper model of this compound of fifteen cuboids, pointed out that it is a faceting of the icosidodecahedron, and I (being me) took that as a challenge to make it myself. Here is my first result, in which all fifteen cuboids have different colors.
I then realized that RW had rendered his in only five colors, so I studied his post more carefully, and made the appropriate adjustments to do the same:
If you’d like to find the Stella page on Facebook, here is a link to it.
RobertLovesPi.net 