First, a cuboctahedron.
Next, its dual, the rhombic dodecahedron.
And, after that, the icosidodecahedron.
And finally, its dual, the rhombic triacontahedron.
All of these rotating images were assembled using Stella 4d, available at http://www.software3d.com/Stella.php.
Each face of a great dodecahedron is a regular pentagon, and each of those pentagonal faces has an icosidodecahedron attached to it, in the figure above. The dual of this figure appears below.
Both images were created with Stella 4d, software available at www.software3d.com/Stella.php.
Music: the first two tracks from the Murder By Death album Like the Excorcist, But More Breakdancing. Please visit their website, http://www.murderbydeath.com, to buy this band’s music and merchandise. While you’re there, I recommend checking their concert calendar, to see if they may be playing near you soon. Murder By Death concerts, which I’ve seen six times now, are not to be missed!
Visuals: rotating polyhedra, all with icosidodecahedral symmetry, generated using Stella 4d: Polyhedron Navigator, which you can try for yourself at http://www.software3d.com/Stella.php. The polyhedra shown are, in order of appearance:
I made this using Stella 4d: Polyhedron Navigator, software you may try for yourself at http://www.software3d.com/Stella.php.
This is the fourth in a series of posts, each of which builds upon the others. The images in the prior three posts were created using Geometer’s Sketchpad and MS-Paint. For this one, I used Stella 4d to project the most recent of these images of each pentagonal face of an icosidodecahedron, and then rendered the triangular faces invisible. (Stella 4d is available for sale, with a free trial download available, at http://www.software3d.com/Stella.php.)
One of the icosidodecahedra is in the center, and the others are attached to its twenty triangular faces.
Software credit: I used Stella 4d to build this. It is available at http://www.software3d.com/Stella.php.
The icosidodecahedron’s 24th stellation is above, and the 32nd, then the 36th, are below.
I made these images using Stella 4d, a program you can find at www.software3d.com/Stella.php.
These were all derived in various ways from the polyhedra seen in the last two posts. The rest are smaller at first, but each can be enlarged with a single click of your mouse. Each of them has icosidodecahedral symmetry.
I used Stella 4d to make these images, and you can find that program at http://www.software3d.com/Stella.php.
Click on the smaller pictures, if you wish to enlarge them, one at a time.
Those last two were duals of each other. The next two are as well.
These next two are duals, as are the pair that follows them.
I’ll finish with one more dual pair.
All of these were made using Stella 4d: Polyhedron Navigator, which is available at http://www.software3d.com/Stella.php.
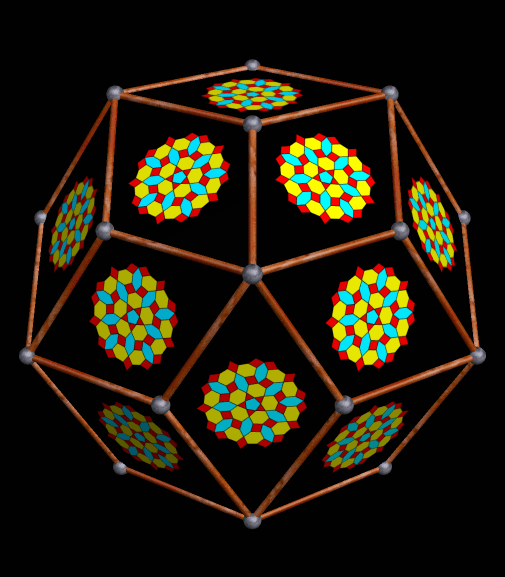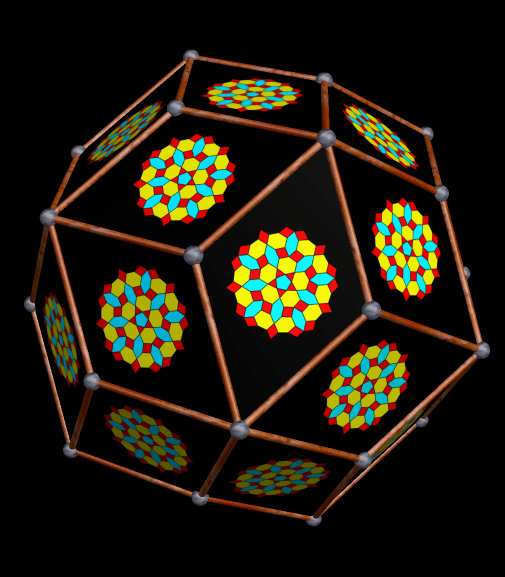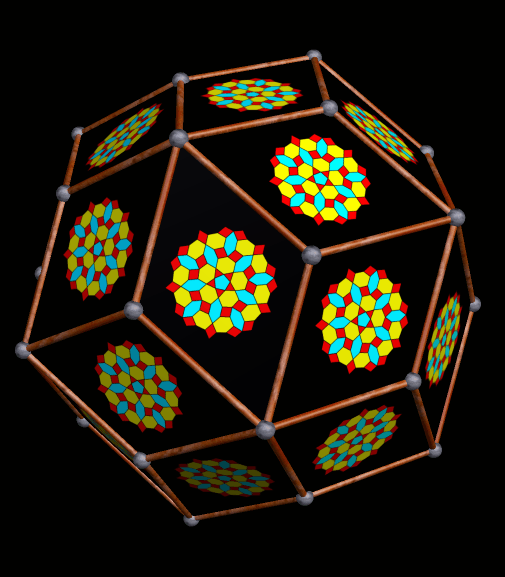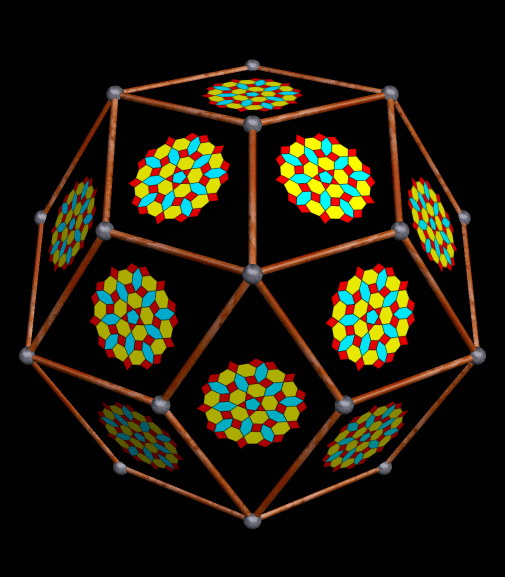
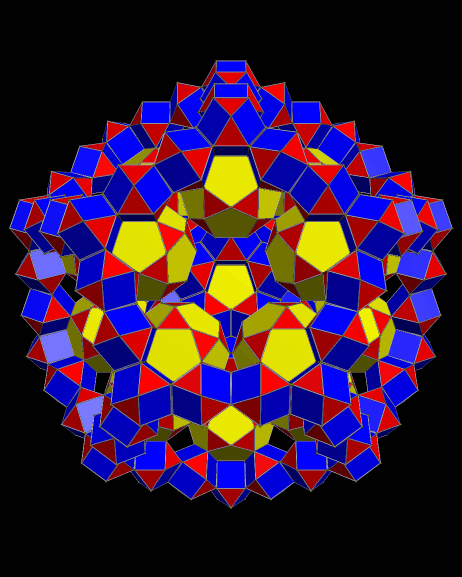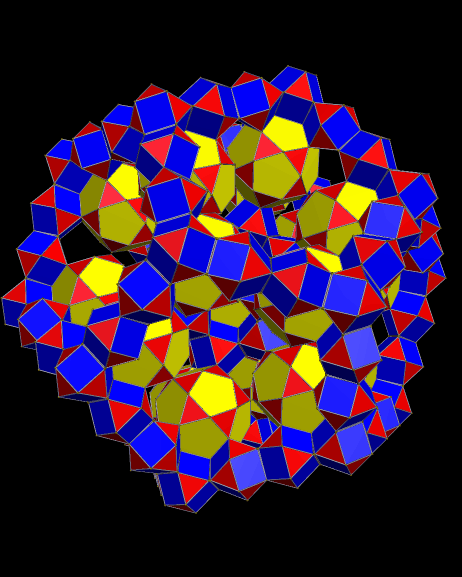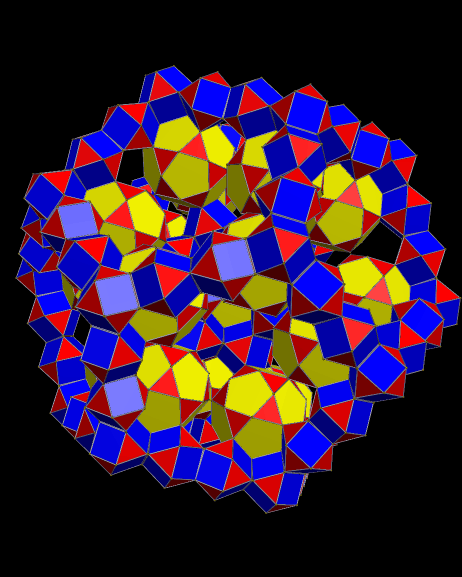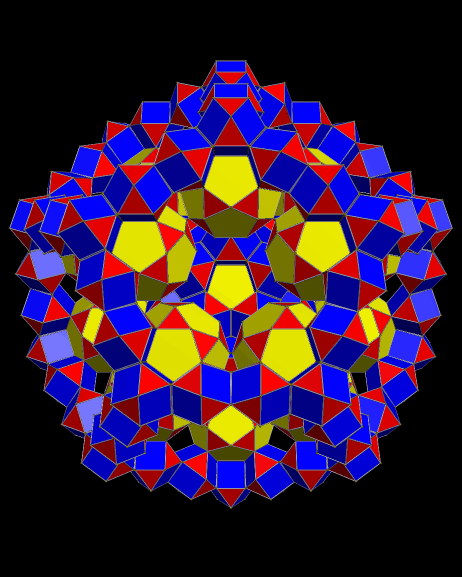
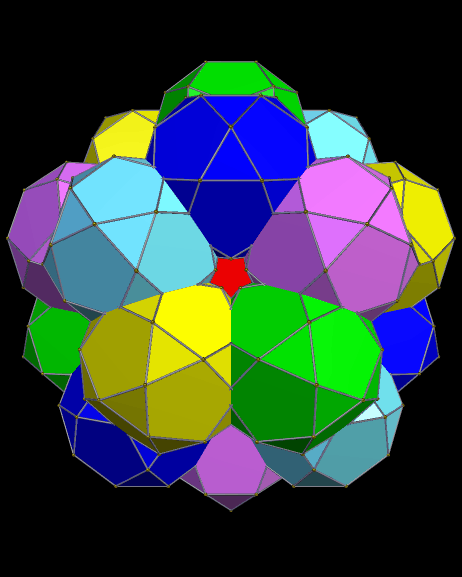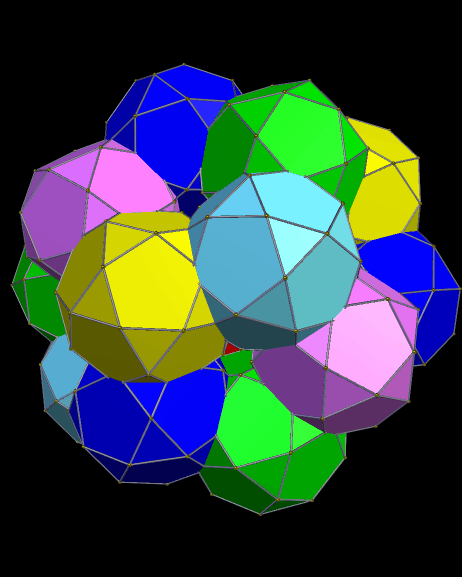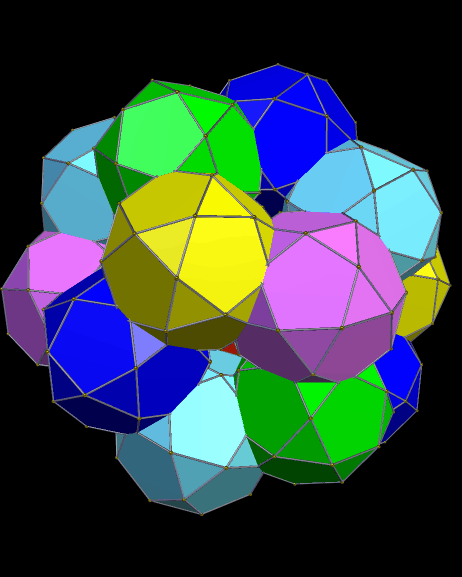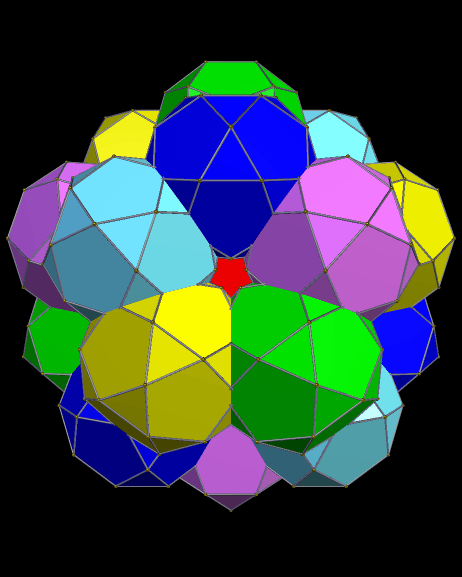
To make this polyhedron using Stella 4d: Polyhedron Navigator (a program which is available at this website), I started with an icosidodecahedron, augmented all faces with prisms of height 1.6 times greater than their bases’ edge length, and then took the convex hull of the result. I’m proposing it as a candidate for the loosely defined group of polyhedra called near-misses to the 92 Johnson solids: convex polyhedra which are almost, but not quite, Johnson solids, due to slight irregularity in some of their faces.
In this case, the pentagons and green triangles are regular, and have the same edge length. The blue triangles, however, are isosceles, with vertex angles of ~67.6687 degrees. The yellow almost-squares are actually rectangles, with edges next to blue triangles which are ~2.536% longer than the edges next to pentagons or green triangles.
I stumbled upon this design earlier today, while simply exploring polyhedra more-or-less randomly, using Stella. Below is the prototype I found at that time, which I merely made a .gif of, but did not perform measurements on.
In this prototype, the most significant difference I can detect is in the yellow faces, which are trapezoids, rather than rectangles, since the pentagon edge-length is slightly longer than that of the green triangles.
Stella has a “try to make faces regular” function built-in to try to help improve upon polyhedra such as these, but here’s what happens when that function is used on the first polyhedron shown above:
Behold! It worked — all of the faces are perfectly regular. However, that caused another problem to appear, and you can see it most easily by looking at the blue triangle-pairs: this polyhedron is slightly non-convex. It’s also easily described as a truncated dodecahedron, with each of the twelve decagonal faces augmented by a pentagonal rotunda.
I’ll show this to some other people who are polyhedron-experts, and will update this post with what I find after I’ve talked to them. My questions for them, as usual in such situations, are two in number:
1. Has this polyhedron been found before?
2. Is it close enough to regularity to qualify for “near-miss” status?
If it hasn’t been found before, but is judged unworthy of “near-miss” status, it will at least join the newly-described group I call “near near-misses” — polyhedra which don’t quite qualify for near-miss status, by visual inspection. Obviously, this new group’s definition is even more “fuzzy” than that of the near-misses, but there is a need for such a category, nonetheless.
[Update: Robert Webb, who wrote Stella 4d (and is not the blogger here, despite our sharing a first name), has seen this before, so it isn’t an original discovery of mine. He doesn’t accept it as a near-miss on the grounds that it naturally “wants” to be non-convex, as seen in the last of the three images in this post, and I agree with his reasoning. I’m therefore considering this to be a “near-near-miss.”]
RobertLovesPi.net 