For any given regular convex polygon, how many star polygons exist?
That’s the beginning. Here are two more:
Since the pattern continues in this manner, it is easy to find the number of possible star polygons for a regular polygon with n sides. First, if (and only if) n is odd, add one. Next, divide by two. Lastly, subtract two, and you have your answer.
Much work has been done on the medians of triangles: segments that connect vertices with the midpoints of opposite sides. This morning, I decided to explore what happens if the trideans are examined, rather than the medians.
The reason you don’t know the word “tridean” is simple: I just made it up. It’s related to a median, though. To find trideans, you must first trisect, rather than bisect, each side of a triangle. This gives you two equally-spaced points on each side. To form a tridean, simply connect one of those points to the opposite vertex. Every triangle has six trideans, and they split the triangle into a set of non-overlapping polygons, as you can see in the diagram.
When I examined the area of these polygons, I started finding unexpected things right away. As you can see, polygons of the same color in this diagram have the same area, even though they are non-congruent. Moreover, these areas are interesting fractions of the area of the entire triangle. The six yellow triangles, for example, each have 1/21st of the area of the entire triangle. Each blue triangle is 1/70th the area of the large triangle. Each green quadrilateral is 1/14th the area of the large triangle. 21, 70, and 14 have one factor in common: the number seven. Seven? I officially have NO idea why sevens are popping up all over the place in this investigation, but there they are.
The red hexagon in the middle has 1/10th the area of the entire triangle, and this number surprised me as well.
The three orange pentagons took a little more work. As you can see, dividing the area of the large triangle by the area of one of these orange pentagons yields 9.5454, with the “54” repeating. This decimal is 105/11. (Eleven?) At least 105 has three as a factor (as does 21, from earlier); three is the number I expected to pop out all over the place, but it shows up little in this investigation. However, what are the other factors of 105? There’s five — and, yet again, seven.
These sevens are everywhere in this thing, and I have no idea why.
Now, of course, I have proven none of this. This is merely a demonstration and explanation of something I think is a new discovery. I did change the shape of the triangle many ways, as a test, and each of these area ratios remained constant.
If anyone can shed some light on any of this — especially all these sevens — please comment.
A regular polygon has some number of sides (n), and its sides and diagonals form a certain number of triangles (t).
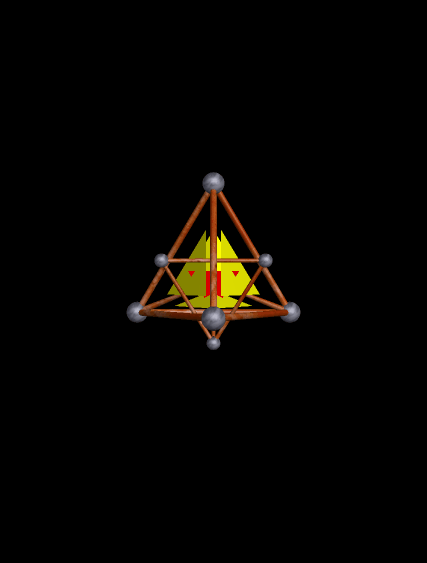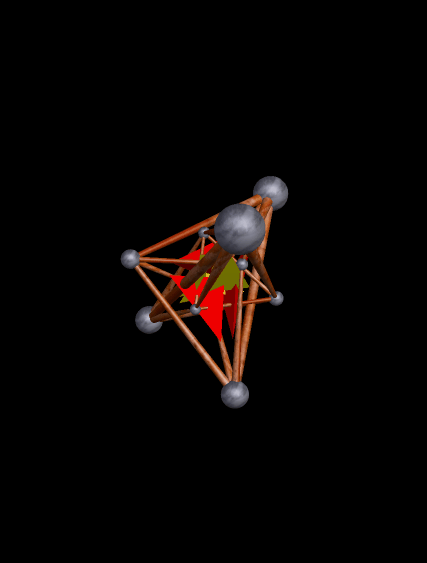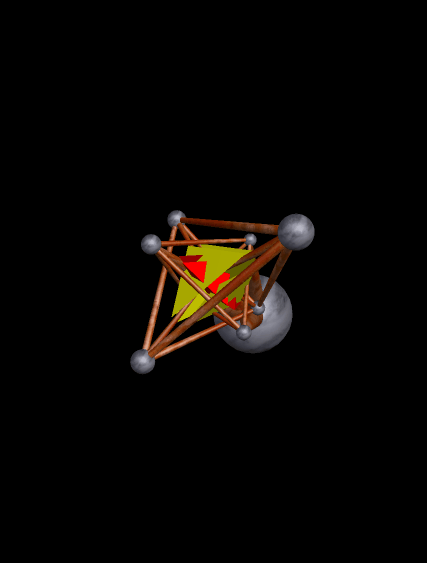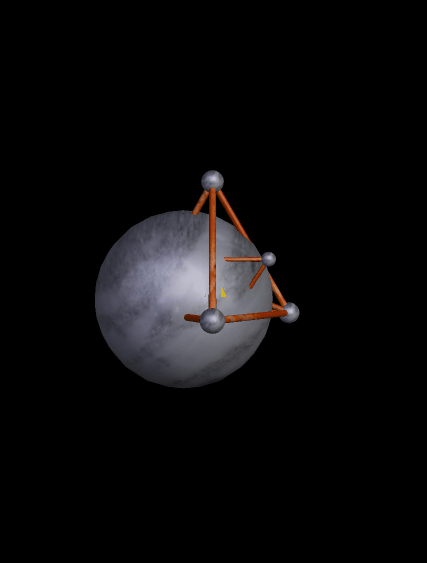
For a triangle, n=3 and t=1.
For a square, n=4. There are four triangles congruent to the one shown in orange, and four more like the one shown in light blue, so adding these gives t=8.
For a pentagon, with n=5, there are five of the purple triangles, five of the green triangles, five of the red triangles, and five of the yellow triangles, for a total of t=20.
For a hexagon, there are two of the orange triangles, six of the yellow ones, twelve of the red ones, six of the light blue ones, twelve of the purple ones, twenty-four of the green ones, twelve of the dark blue ones, six of the grey ones, six of the black ones, twelve of the pink ones, and six of the brown ones. That’s 2+6+12+6+12+24+12+6+6+12+6 = t = 104.
Three yields one, four yields eight, five yields 20, and six yields 104. At the moment, I don’t have the patience to count the triangles in a heptagon, but it would clearly be, well, quite a few.
There may or may not be a formula for this; any pattern eludes me, so far. I am reminded of the alkane series in chemistry: one isomer each of methane, ethane, and propane, two of butane, three of pentane, and so on to 75 for decane, and beyond. All efforts to find a formula for the number of isomers, in terms of the number of carbon atoms, have failed (to date). For now, these are both filed under “unsolved problems.”
UPDATE: A friend of mine has shown me that this polygon problem has, in fact, been solved, and he provided this link: http://oeis.org/A006600 — apparently I missed some of the triangles in the pentagon (the red and yellow combined, for example), as well as the hexagon. The correct numbers for those two polygons are 35 and 110, respectively. Aside from this update, I’m not changing the rest, for I need reminders of my own fallibility. This will do nicely.
I am confident that this “beat frequency” effect will continue as this process of combining trigonometric and exponential functions continues.
The simplest polyhedron is the tetrahedron, and it is self-dual. The compound of two tetrahedra puts these duals together, and is most often called the Stella Octangula, a name Johannes Kepler gave it in the early 17th Century.
In hyperspace, or 4-space, the simplest polychoron is the pentachoron, or 5-cell. Like the tetrahedron in 3-space, it is also self-dual. Here is the compound of two of them: hyperspace’s version of the Stella Octangula.
Website to find the software used to make these images: www.software3d.com/stella.php
Now that the latest version of Stella 4d allows users to make rotating .gifs, I post those here (see the last post for an example). However, before I started blogging on WordPress, I made a blog on Tumblr with many still images produced using earlier versions of Stella. Here is an example:
The link above is to that blog’s archive — just click on any small pic there to make it larger. Unlike other Tumblr-blogs of mine, this one has no reblogged material — it was the banality of reblogging, you see, that drove me from Tumblr in the first place.
Info on getting/trying Stella 4d for yourself: www.software3d.com/stella.php
The most familiar polychoron, to those who have heard of any of them, is the hypercube, or tesseract. It is analogous to the cube, but in four dimensions. All polychora are four-dimensional. With numbers of spatial dimensions above four, only the term “polytope” is used. Polyhedra are 3-polytopes, and polychora are 4-polytopes.
This is a three-dimensional projection of a tesseract, as it rotates in hyperspace, casting a “shadow” into our space:
In three dimensions, a cube is not the simplest polyhedron. A tetrahedron (a regular triangle-based pyramid) is simpler.
The simplest polychoron is composed of five tetrahedral cells, and is analogous to the tetrahedron, but in hyperspace. Here is a rotating “hypertetrahedron.”
There are even more names for these two polychora, based on the number of cells (cubes or tetrahedra). The tesseract/hypercube is composed of eight cubes, so it is called the 8-cell, as well as the octachoron. The preferred names for the hypertetrahedron are the 5-cell and the pentachoron, as it is composed of five (tetrahedral) cells.
Just as there are other Platonic solids not mentioned here, there are other regular polychora as well. The others will be subjects of upcoming posts, and one has already appeared here once (the 120-cell, or hyperdodecahedron), just three posts back.
Software note: these .gifs were made using Stella 4d, which may be purchased, and/or tried for free (on a trial basis), at http://www.software3d.com/Stella.php.
Website to try polyhedra-making software used to make this image: http://www.software3d.com/stella.php
This moving image of a projection of the four-dimensional 120-cell was made using Stella 4d, software you can try for free here: http://www.software3d.com/stella.php
In this polyhedron, there are, easily visible, twenty light blue faces which are equilateral triangles. Inside the polyhedron (and therefore harder to spot) are thirty purple faces which are Golden rectangles, along with twelve large, orange regular pentagonal faces.
To try the software I used to make this polyhedron, please visit www.software3d.com/stella.php.
RobertLovesPi.net 