I wish I remembered exactly how I made this polyhedron, but I don’t. I found it during a “random walk” polyhedral exploration using Stella 4d: Polyhedron Navigator, software you can buy, or try for free, here.
Hexastar Octahedron
8
Tag Archives: octahedron
Open Octahedral Lattice of Cubes and Rhombicosidodecahedra
This pattern could be continued, indefinitely, into space.
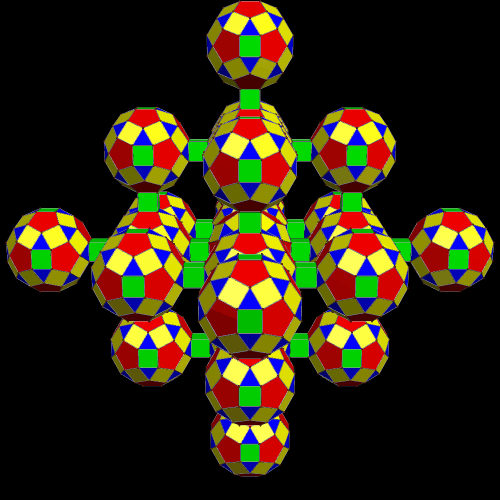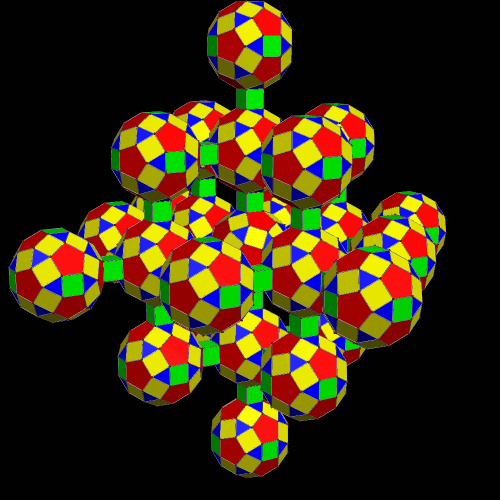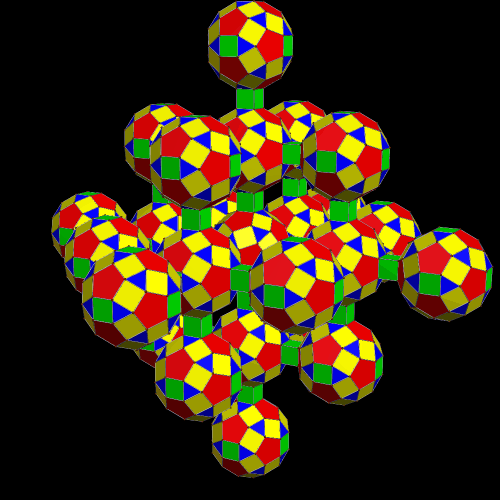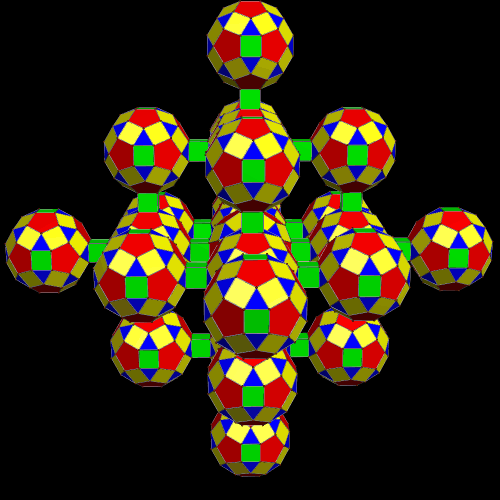
Here is a second view, in rainbow color mode, and with all the squares hidden.
[These images were created with Stella 4d, software you may buy — or try for free — right here.]
The Compounds of Five Octahedra and Five Cubes, and Related Polyhedra
This is the compound of five octahedra, each a different color.
Since the cube is dual to the octahedron, the compound of five cubes, below, is dual to the compound above.
Here are five cubes and five octahedra, compounded together, and shown with the same five colors used above.
This is the same compound, except with all squares/cubes having one color, and triangles/octahedra having another, made by changing the color-scheme used by Stella 4d (the program I use to make these images; it’s available here).
After seeing the two-color version of this ten-part compound, I decided to start stellating it, looking for stellations with an interesting appearance. Here is the 23rd stellation of the ten-part compound, colored by face-type.
Next, the 27th stellation, which is chiral, unlike the stellation showed above.
The 33rd stellation also has an interesting appearance (using, I admit, completely subjective criteria for “interesting”), while still having easily-noticable differences to the stellations shown above.
At the 35th stellation, another interesting chiral polyhedron is found. Unexpectedly, its direction of “twist” appears opposite that seen in the 27th stellation. (It could well be that this “twist-reversal” is a common phenomenon in stellation-series — simply one I have never noticed before.)
Next, the ten-part compound’s 39th stellation.
After the 39th stellation, I entered a sort of “desert,” with many stellations in a row which did not strike me as interesting, often with only tiny differences between one and the next. The 194th stellation, though, I liked.
Although I liked the 194th stellation, I didn’t want to risk trudging through another “desert” like the one which preceded it, so I jumped ahead to the final valid stellation, after which the series “wraps around” to its beginning.
Next, I made another rotating image of this final valid stellation, this time with the color-scheme set to “rainbow color mode.”
I couldn’t resist taking this one stellation further, to see the beginning of the stellation-series, since I knew I might have entered it somewhere in the middle, rather than at the beginning.
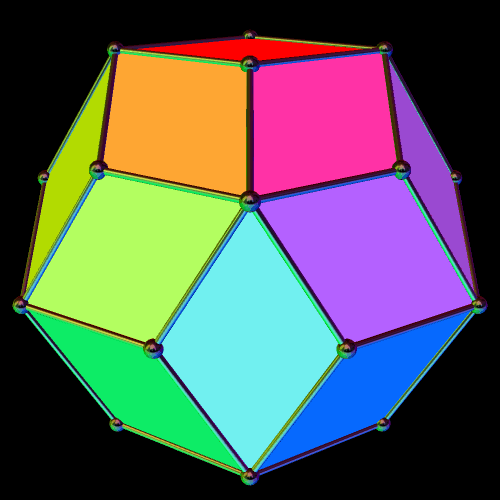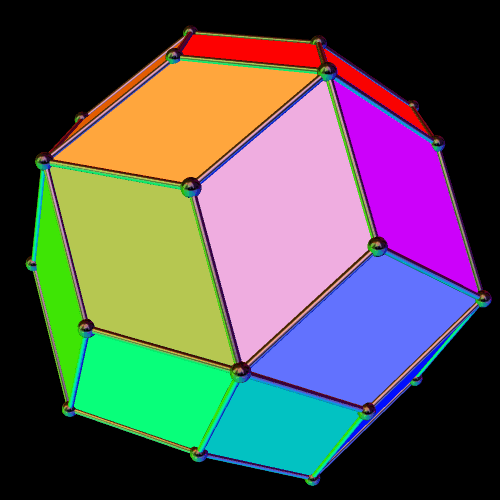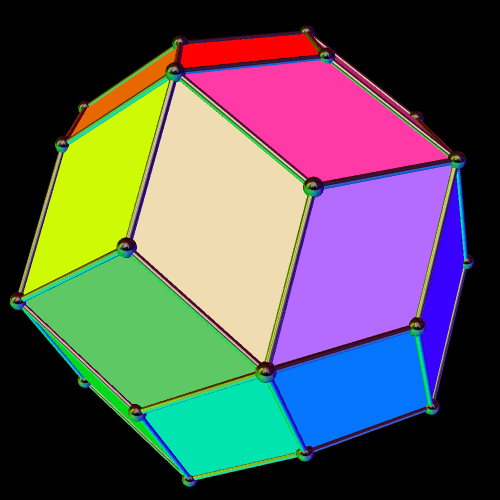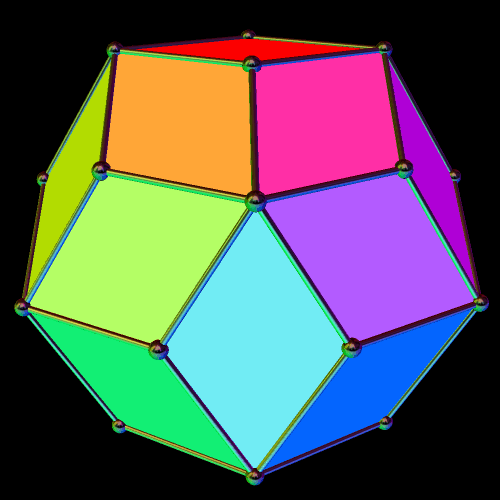
What I found, I immediately recognized as the rhombic triacontahedron. In some ways, this was surprising, and in other ways, it was not. The compound of five cubes is, itself, a stellation of the rhombic triacontahedron — but what I started stellating also included the compound of five octahedra, which, so far as I know, is not part of the rhombic triacontahedron’s (very) long stellation-series. Also, I know what the rhombic triacontahedron’s final stellation looks like, and it isn’t the final stellation shown above, but is, instead, this:
To try to better-understand just what was going on here, I went back, and deliberately left out the five-cube part of the ten-part compound (which is a stellation of the rhombic triacontahedron), which left me just with the compound of five octahedra — and then I had Stella produce this compound’s final stellation.
This was another polyhedron I recognized: the final stellation of the icosahedron. To verify that my memory was correct, I stellated it one more time. Sure enough, this is what I got:
This reminded me that the compound of five octahedra is the second stellation of the icosahedron, helping to explain some of this. I also noticed that the five-octahedron compound can be seen as a faceting of the icosidodecahedron. (The icosidodecahedron is dual to the rhombic triacontahedron, and faceting is the reciprocal function of stellation.) However, I have no idea why the final stellation of the ten-part compound above appears as it does.
It is my opinion that a productive polyhedral investigation usually does more than answer questions; it also raises new ones. At least in my mind, that’s exactly what has happened. Therefore, I think this was a perfectly good way to begin the new year.
Building a Rhombic Enneacontahedron, Using Icosahedra and Elongated Octahedra
With four icosahedra, and four octahedra, it is possible to attach them to form this figure:
This figure is actually a rhombus, but the gap between the two central icosahedra is so small that this is hard to see. To remedy this problem, I elongated the octahedra, thereby creating this narrow rhombus:
It is also possible to use the same collection of polyhedra to make a wider rhombus, as seen below.
These aren’t just any rhombi, either, but the exact rhombi found in the polyhedron below, the rhombic enneacontahedron. It has ninety rhombi as faces: sixty wide ones, and thirty narrow ones.
As a result, it is possible to use the icosahedra-and-elongated-octahedra rhombi, above, to construct a rhombic enneacontahedron made of these other two polyhedra. The next several images show it under construction (I “built” it using Stella 4d, available at this website), culminating with the complete figure.
Lastly, I made one more image — the same completed shape, but in “rainbow color mode.”
A Compound of the Octahedron, and a Pyritohedral Dodecahedron
This compound is the first I have seen which combines a Platonic solid (the blue octahedron) with a pyritohedral modification of a Platonic solid. Here’s what a pyritohedral dodecahedron looks like, by itself:
Stella 4d: Polyhedron Navigator was used to make these — software you can try right here: http://www.software3d.com/Stella.php.
A Rhombic Dodecahedron, Built from Icosahedra and Octahedra
I assembled this using Stella 4d, software available here.
Two Different Forty-Part Polyhedral Compounds
The polyhedron above is a compound of twenty cubes and twenty octahedra, colored by symmetry-based face-type. If the same compound is viewed in “rainbow color mode,” it looks like this:
With this particular compound, though, there are two versions — without taking coloring into consideration at all. The other version simply has the twenty cubes and twenty octahedron in a different, but still symmetrical, arrangement:
The compound above uses this second arrangement, colored by face type, and the next image is the same (second) compound, but in “rainbow color mode.”
These rotating polyhedral images were made with Stella 4d, software you can try for yourself, right here.
Two Polyhedral Meta-Compounds
The polyhedral compound above is actually a compound of two compounds: the compound of three cubes (red, yellow, and blue), as well as the cube/octahedron base/dual compound (green and purple). The dual of this five-part compound is shown below, still with the cube/octahedron compound in green and purple (it is its own dual), and with the three parts of the compound of three octahedra in red, yellow, and blue.
I created these using the “add/blend from memory” function of Stella 4d: Polyhedron Navigator, one of this program’s capabilities which I have only recently begun to explore. You may try this software for yourself, for free, right here.
Combining Octahedral and Icosahedral Symmetry to Form Pyritohedral Symmetry
Pyritohedral symmetry, seen by example both above and below, is most often described at the symmetry of a volleyball:
[Image of volleyball found here.]
To make the rotating polyhedral compound at the top, from an octahedron and an icosahedron, I simply combined these two polyhedra, using Stella 4d, which may be purchased (or tried for free) here.
In the process, I demonstrated that it is possible to combine a figure with octahedral (sometimes called cuboctahedral) symmetry, with a figure with icosahedral (sometimes called icosidodecahedral) symmetry, to produce a figure with pyritohedral symmetry.
Now I can continue with the rest of my day. No matter what happens, I’ll at least know I accomplished something.
The Second of Dave Smith’s “Bowtie” Polyhedral Discoveries, and Related Polyhedra
Dave Smith discovered the polyhedron in the last post here, shown below, with the faces hidden, to reveal how the edges appear on the back side of the figure, as it rotates. (Other views of it may be found here.)
So far, all of Smith’s “bowtie” polyhedral discoveries have been convex, and have had only two types of face: regular polygons, plus isosceles trapezoids with three equal edge lengths — a length which is in the golden ratio with that of the fourth side, which is the shorter base.
He also found another solid: the second of Smith’s polyhedral discoveries in the class of bowtie symmetrohedra. In it, each of the four pentagonal faces of the original discovery is augmented by a pentagonal pyramid which uses equilateral triangles as its lateral faces. Here is Smith’s original model of this figure, in which the trapezoids are invisible. (My guess is that these first models, pictures of which Dave e-mailed to me, were built with Polydrons, or perhaps Jovotoys.)
With Stella 4d (available here), the program I use to make all the rotating geometrical pictures on this blog, I was able to create a version (by modifying the one created by via collaboration between five people, as described in the last post) of this interesting icositetrahedron which shows all four trapezoidal faces, as well as the twenty triangles.
Here is another view: trapezoids rendered invisible again, and triangles in “rainbow color” mode.
It is difficult to find linkages between the tetrapentagonal octahedron Smith found, and other named polyhedra (meaning I haven’t yet figured out how), but this is not the case with this interesting icositetrahedron Smith found. With some direct, Stella-aided polyhedron-manipulation, and a bit of research, I was able to find one of the Johnson solids which is isomorphic to Smith’s icositetrahedral discovery. In this figure (J90, the disphenocingulum), the trapezoids of this icositetrahedron are replaced by squares. In the pyramids, the triangles do retain regularity, but, to do so, the pentagonal base of each pyramid is forced to become noncoplanar. This can be difficult to see, however, for the now-skewed bases of these four pyramids are hidden inside the figure.
Both of these solids Smith found, so far (I am confident that more await discovery, by him or by others) are also golden polyhedra, in the sense that they have two edge lengths, and these edge lengths are in the golden ratio. The first such polyhedron I found was the golden icosahedron, but there are many more — for example, there is more than one way to distort the edge lengths of a tetrahedron to make golden tetrahedra.
To my knowledge, no ones knows how many golden polyhedra exist, for they have not been enumerated, nor has it even been proven, nor disproven, that their number is finite. At this point, we simply do not know . . . and that is a good way to define areas in mathematics in which new work remains to be done. A related definition is one for a mathematician: a creature who cannot resist a good puzzle.
RobertLovesPi.net 