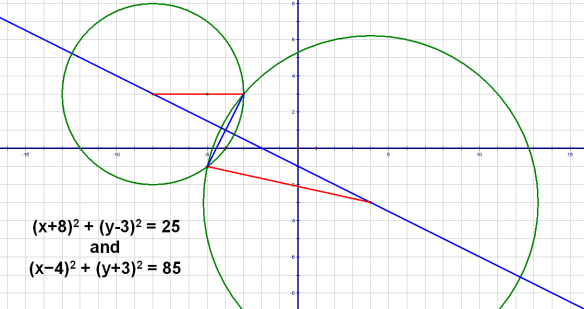
Before attempting to create a method for solving this problem with any given circles, I’m going to attempt solving it for this arbitrary pair of circles. The small circle has radius 5, is centered at (-8,3), and has the equation (x+8)² + (y-3)² = 25. The larger circle has a radius of √85, is centered at (4,-3), and has the equation (x-4)² + (y+3)² = 85.

The first thing I will do is add 60 to each side of the equation of the smaller circle, changing that equation to (x+8)² + (y-3)² + 60 = 85. There are now two equations with 85 on one side, so I will set their other sides equal to each other:  (x+8)² + (y-3)² + 60 = (x-4)² + (y+3)². Next, I square each term in parentheses, turning this equation into x² + 16x +64 + y² -6y +9 + 60 = x² – 8x +16 + y² + 6y +9. After x², y², and 9 are each cancelled from each side, the equation looks like this:  16x +64 – 6y +60 = -8x + 16 + 6y. This simplifies further to -12y + 124= -24x +16, then -12y = -24x -108, then, after dividing both sides -12, that yields the simplified equation for the straight line y = 2x + 9. Any solutions which exist, therefore, must be found on the line y = 2x + 9.

(x+8)² + (y-3)² = 25 is the equation of the smaller circle, and substituting 2x + 9 for y in this equation turns it into (x+8)² + (2x + 9 – 3)² = 25, which is equivalent to (x+8)² + (2x + 6)² = 25. By squaring the terms in parentheses found in this last equation, this turns into x² + 16x +64 + 4x² + 24x + 36 = 25, which simplifies further to 5x² +40x + 75 = 0, and then x² +8x + 15 = 0.

Applying the quadratic formula (because I don’t enjoy factoring trimonials) to this last equation, x = {-8 ± sqrt[64 – (4)(1)15)]}/2, which means that x has two values in this case:  x = (-8 + 2)/2 = -6/2 = -3, and x = (-8 – 2)/2 = -10/2 = -5. When x = -3, then y = 2(-3) +9 = -6 + 9 = 3, so one solution is the ordered pair (-3,3). By constrast, when x = -5, then y = 2(-5) +9 = -10 + 9 = -1, so the other solution is the ordered pair (-5,-1).

For other circle-pairs, the method is the same, but appropriate substitutions will need to be made in the numbers with which I started, likely leading, of course, to different answers. For some pairs of circles, the quadratic formula will not yield two real ordered pairs as solutions. If all values of x and y are nonreal, this simply means that the two circles do not touch at all. If, on the other hand, only ordered pair can be found as a solution, this means the circles are tangent to each other — touching only at a single point.