Shown above: the compound of the icosahedron and the rhombic dodecahedron. Below is its dual, the compound of the dodecahedron and the cuboctahedron.
Both these compounds were created using the “add/blend polyhedron from memory” function in Stella 4d: Polyhedron Navigator. To check out this program for yourself, just follow this link.
The dual to this cluster-polyhedron appears below. Both virtual models were created using Stella 4d: Polyhedron Navigator, software available here.
For years, I have used Zometools (sold here: http://www.zometool.com) to teach geometry. The constructions for the icosahedron and dodecahedron are easy to teach and learn, due to the use of short reds (R1s) and medium yellows (Y2s) for radii for the two of them, as shown below, with short blue (B1) struts as edges for both polyhedra.
Unexpectedly, a student (name withheld for ethical and legal reasons) combined the two models, making this:
I saw it, and wondered if the two combined Platonic solids could be expanded along the edges, to stellate both polyhedra, with medium blues (B2s), to form the great and small stellated dodecahedron. By trying it, I found out that this would require intersecting blue struts — so a Zomeball needed to be there, at the intersection. Trying, however, only told me that no available combination would fit. After several more attempts, I doubled each edge length, and added some stabilizing tiny reds (R0s), and found a combination that would work, to form a compound of the great and small stellated dodecahedron in which both edge lengths would be equal. In the standard (non-stellated) compound of the icosahedron and dodecahedron, in which the edges are perpendicular, they are unequal in length, and in the golden ratio, which is how that compound differs from the figure shown directly above.
Here’s the stabilized icosahedral core, after the doubling of the edge length:
This enabled stellation of each shape by edge-extension. Each edge had a length twice as long as a B2 added to each side — and it turns out, I discovered, that 2B2 in Zome equals B3 + B0, giving the golden ratio as one of three solutions solution to x² + 1/x = 2x (the others are one, and the golden ratio’s reciprocal). After edge-stellation to each component of the icosahedron/dodecahedron quasi-compound, this is what the end product looked like. This required assembling the model below at home, where all these pictures were taken, for one simple reason: this thing is too wide to fit through the door of my classroom, or into my car.
Here’s a close-up of the central region, as well.
The snub cube and its dual make an attractive compound. Since the snub cube is chiral, its chirality is preserved in this compound.
If you examine the convex hull of this compound, you will find it to be chiral as well.
Here is the mirror image of that convex hull:
These two convex hulls, of course, have twin, chiral, duals:
The two chiral convex hulls above (the red, blue, and yellow ones), made an interesting compound, as well.
This is also true of their chiral duals:
I next stellated this last figure numerous times (I stopped counting at ~200), to obtain this polyhedron:
After seeing this, I wanted to know what its dual would look like — and it was a nice polyhedron on which to end this particular polyhedral journey.
I make these transformations of polyhedra, and create these virtual models, using a program called Stella 4d. It may be purchased, or tried for free, at http://www.software3d.com/Stella.php.
In this model, the usual presentation of the icosahedron/dodecahedron dual compound has been altered somewhat. The “arms” of star pentagons have been removed from the dodecahedron’s faces, and the icosahedron is rendered “Leonardo-style,” with smaller triangles removed from each of the faces of the icosahedron, with both these alterations made to enable you to see the model’s interior structure. Also, the dodecahedron is slightly larger than usual, so that its edges no longer intersect those of the icosahedron.
This model was made using Stella 4d, software you can obtain for yourself, with a free trial download available, at http://www.software3d.com/Stella.php.
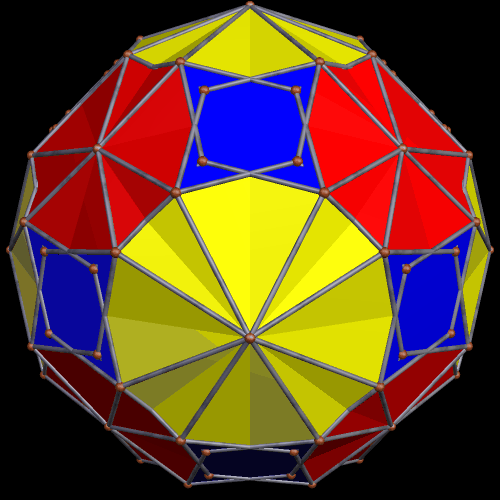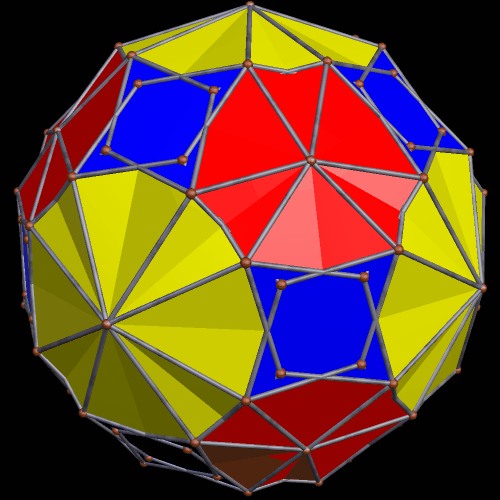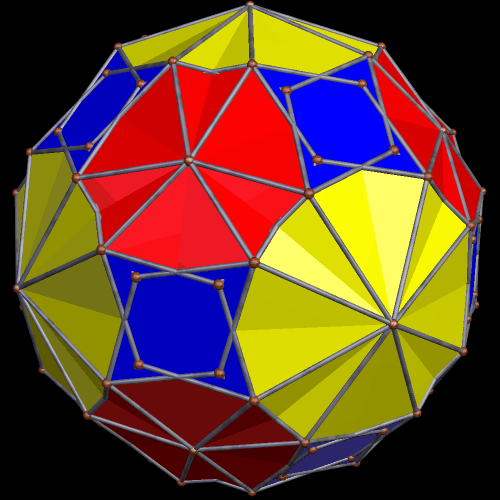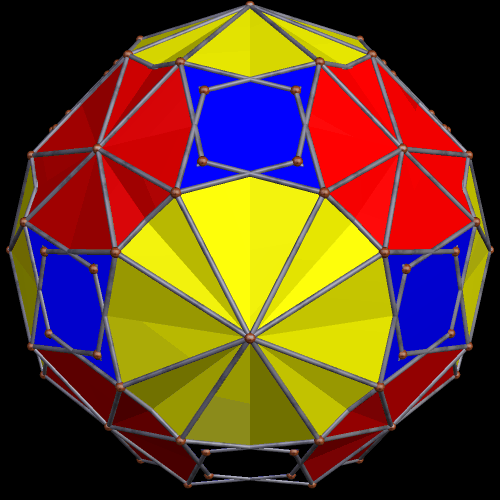
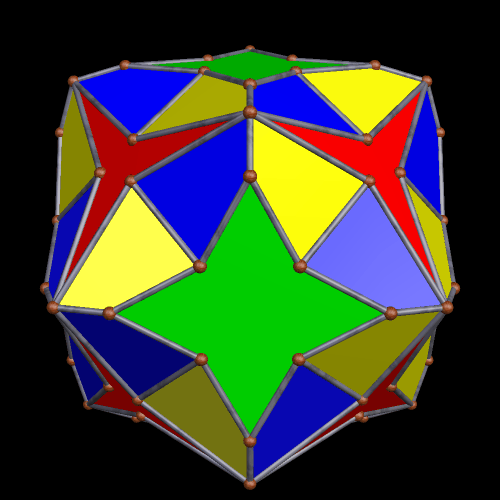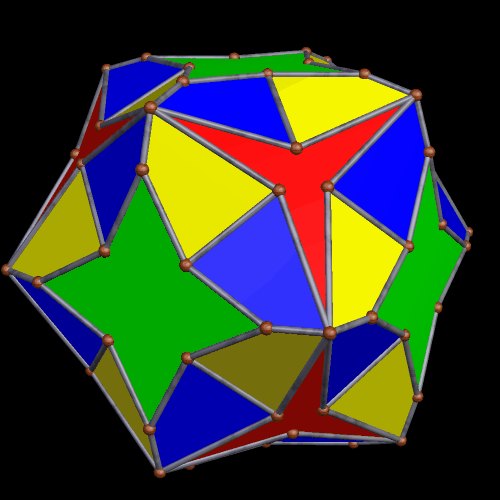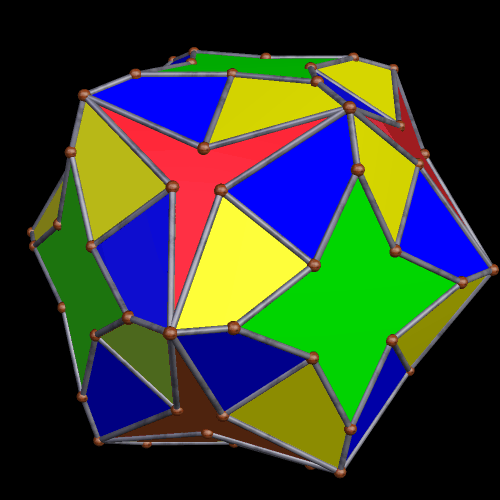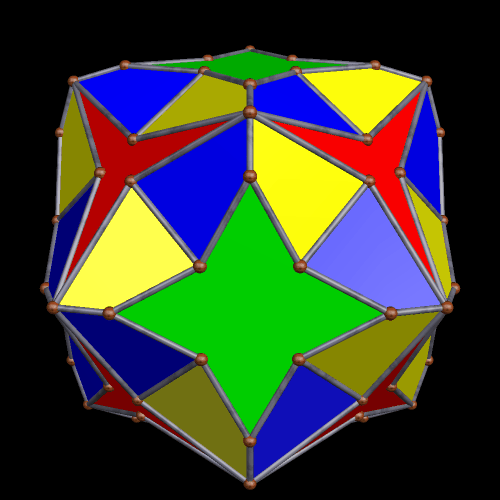
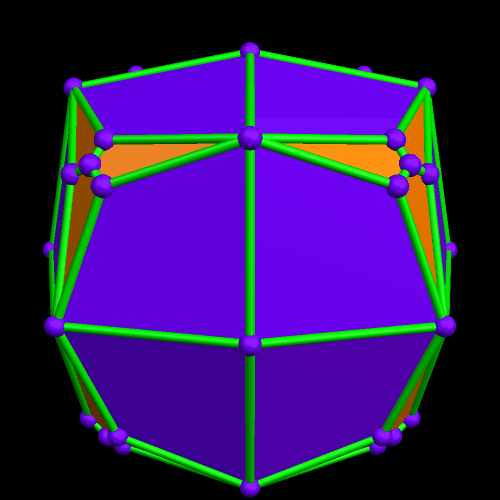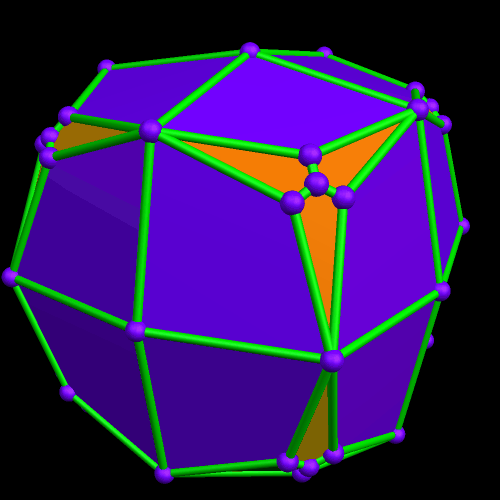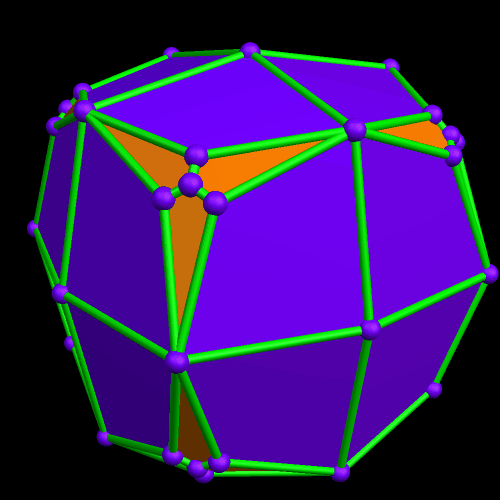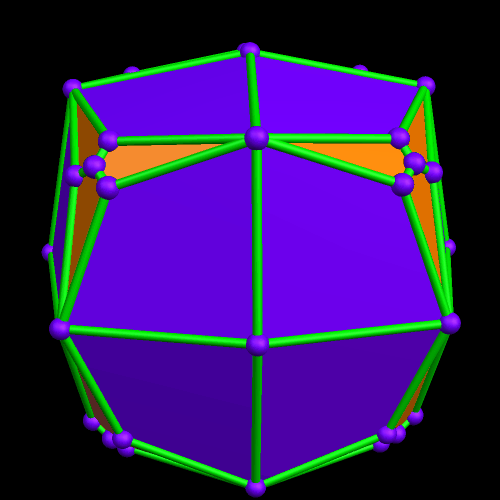
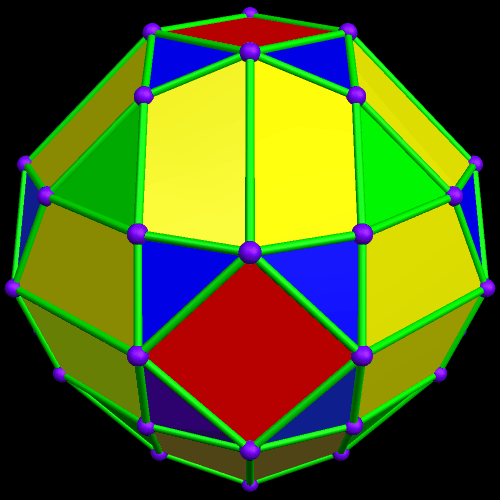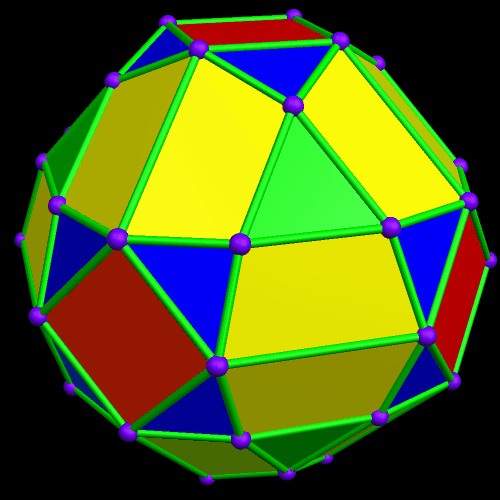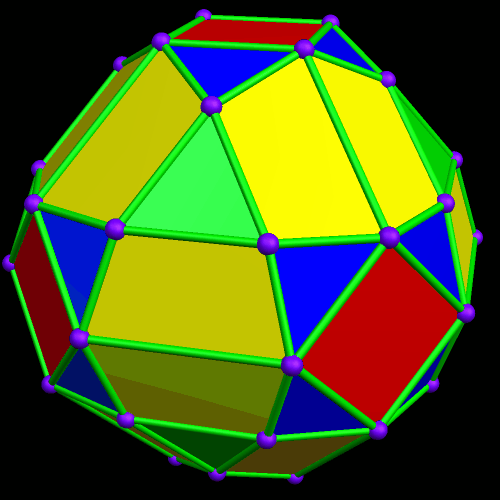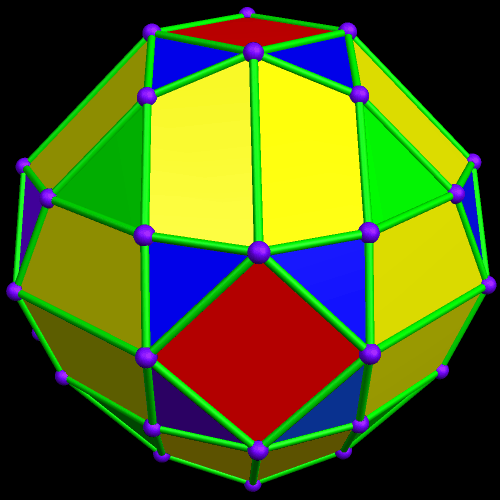
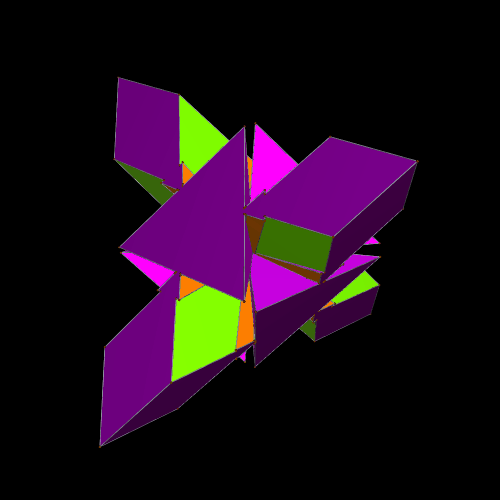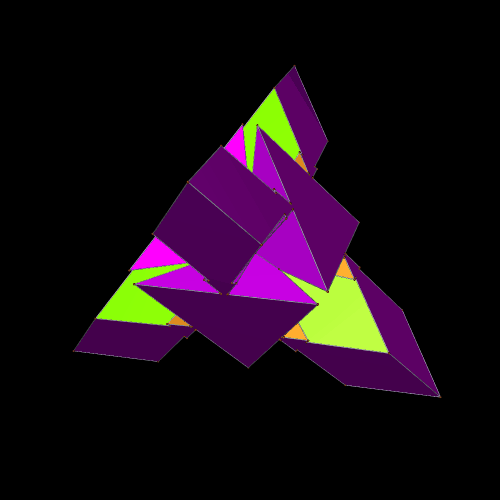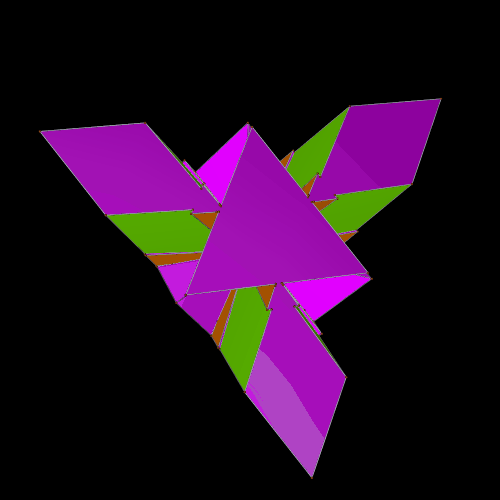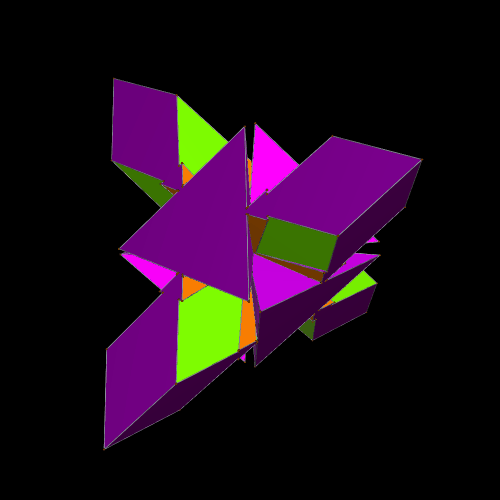In the post directly before this one, the third image was an icosahedral cluster of icosahedra. Curious about what its convex hull would look like, I made it, and thereby saw the first polyhedron I have encountered which has 68 triangular faces.
Still curious, I next examined this polyhedron’s dual. The result was an unusual 36-faced polyhedron, with a dozen irregular heptagons, and two different sets of a dozen irregular pentagons.
Stella 4d (the program I used to make all these images), which is available at http://www.software3d.com/Stella.php, has a “try to make faces regular” function, and I tried to use it on this 36-faced polyhedron. When making the faces regular is not possible, as was the case this time, it sometimes produce surprising results — and this turned out to be one of these times.
The next thing I did was to examine the dual of this latest polyhedron. The result, a cluster of tetrahedra and triangles, was completely unexpected.
The next alteration I performed was to create the convex hull of this cluster of triangles and tetrahedra.
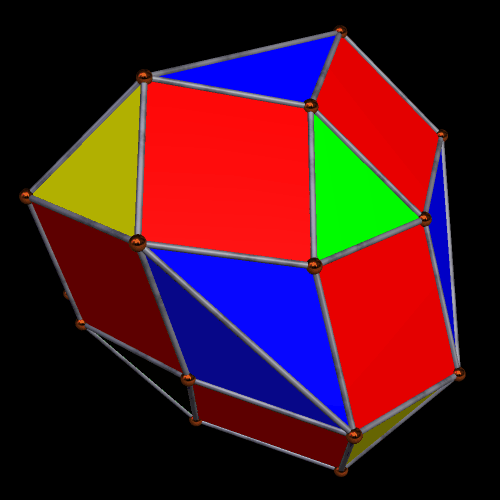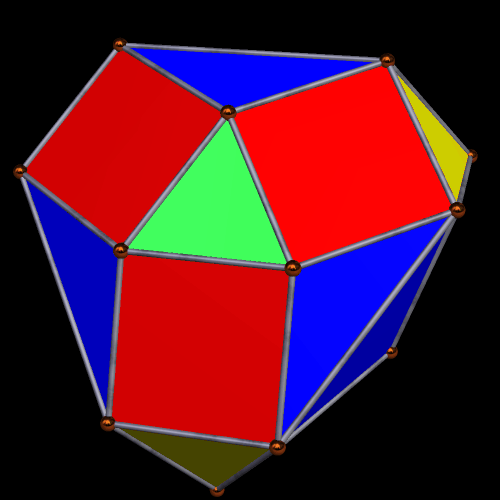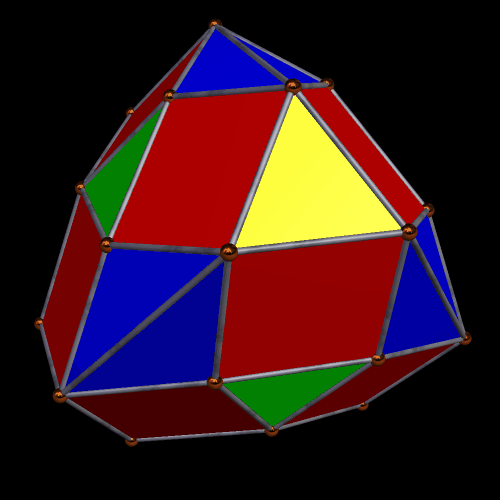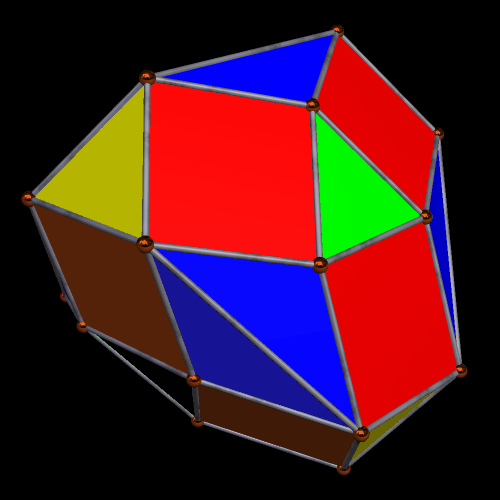
Having seen that, I wanted to see its dual, so I made it. It turned out to have a dozen faces which are kites, plus another dozen which are irregular pentagons.
Next, I tried the “try to make faces regular” function again — and, once more, was surprised by the result.
Out of curiosity, I then created this latest polyhedron’s convex hull. It turned out to have four faces which are equilateral triangles, a dozen other faces which are isosceles triangles, and a dozen faces which are irregular pentagons.
Next, I created the dual of this polyhedron, and it turns out to have faces which, while not identical, can be described the same way: four equilateral triangles, a dozen other isosceles triangles, and a dozen irregular pentagons — again. To find such similarity between a polyhedron and its dual is quite uncommon.
I next attempted the “try to make faces regular” function, once more. Stella 4d, this time, was able to make the pentagons regular, and the triangles which were already regular stayed that way, as well. However, to accomplish this, the twelve other isosceles triangles not only changed shape a bit, but also shifted their orientation inward, making the overall result a non-convex polyhedron.
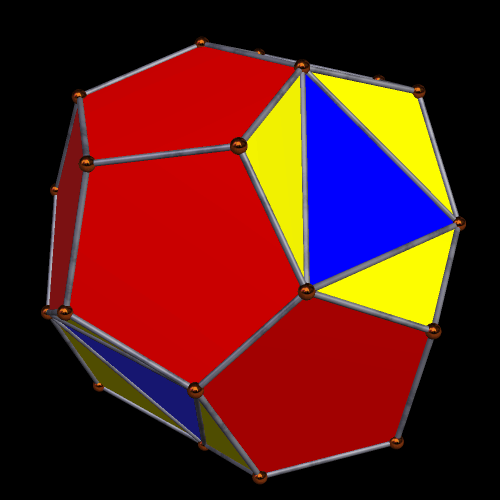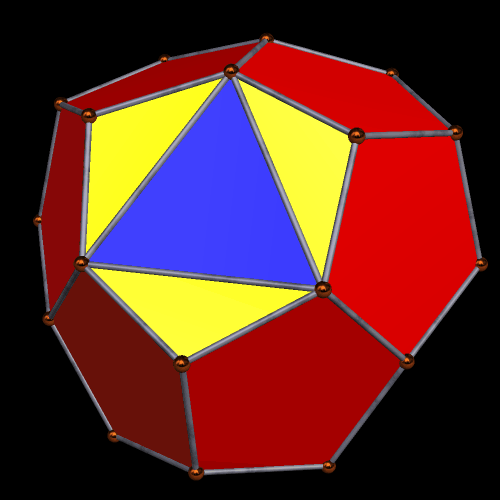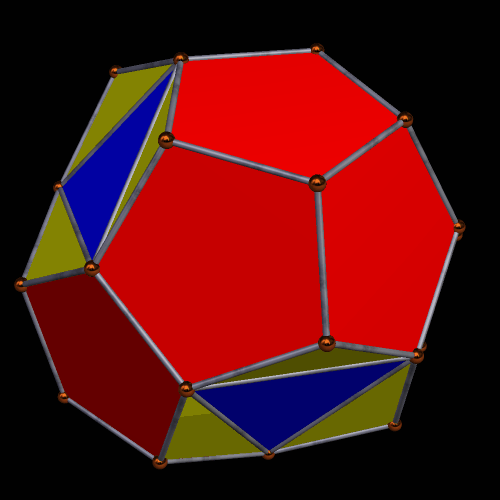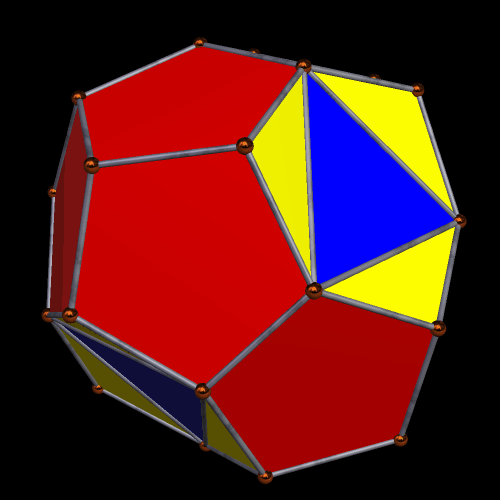
Having a non-convex polyhedron on my hands, the next step was obvious: create its convex hull. One more, I saw a polyhedron with faces which were four equilateral triangles, a dozen other isosceles triangles, and a dozen regular pentagons.
I then created the dual of this polyhedron, and, again, found myself looking at a polyhedron with, as faces, a dozen irregular pentagons, a dozen identical isosceles triangles, and four regular triangles. However, the arrangement of these faces was noticeably different than before.
Given this difference in face-arrangement, I decided, once more, to use the “try to make faces regular” function of Stella 4d. The results were, as before, unexpected.
Next, I created this latest polyhedron’s dual.
At no point in this particular “polyhedral journey,” as I call them, had I used stellation — so I decided to make that my next step. After stellating this last polyhedron 109 times, I found this:
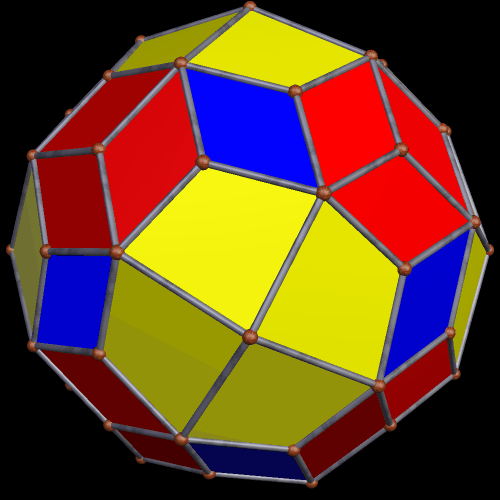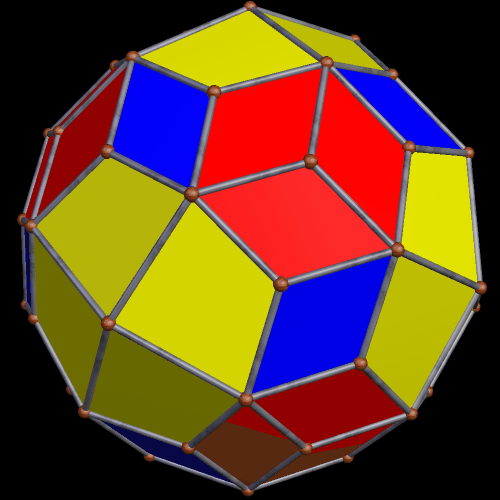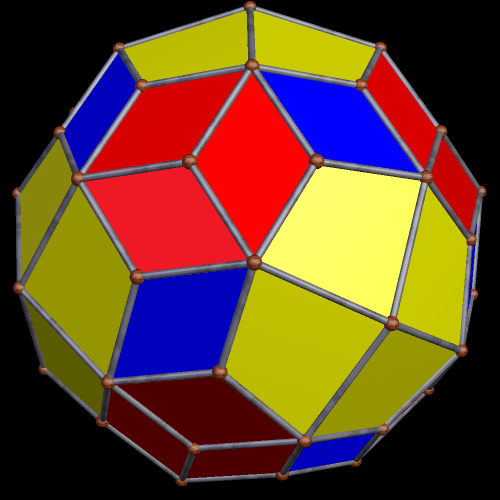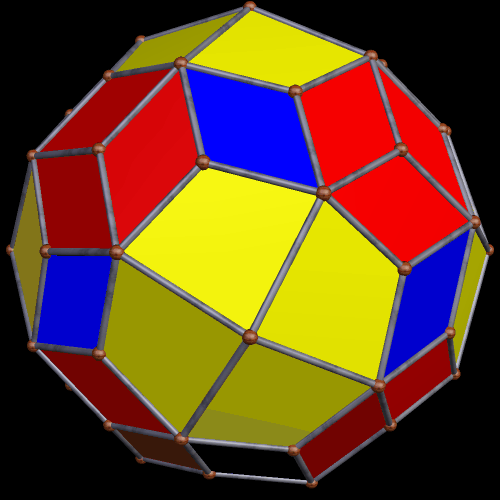
I then created the dual of this polyhedron. The result, unexpectedly, had a cuboctahedral appearance.
A single stellation of this latest polyhedron radically altered its appearance.
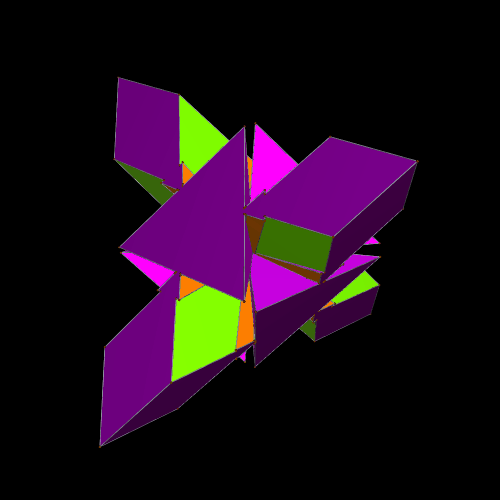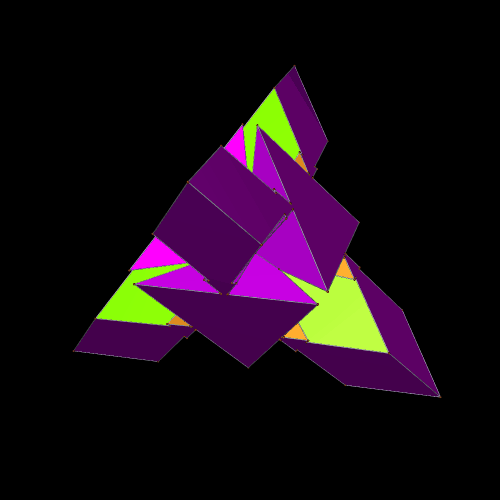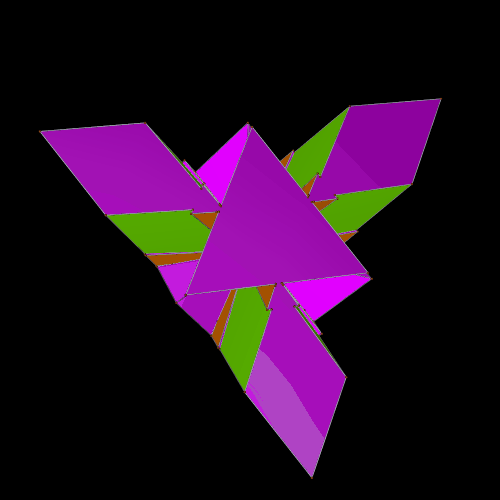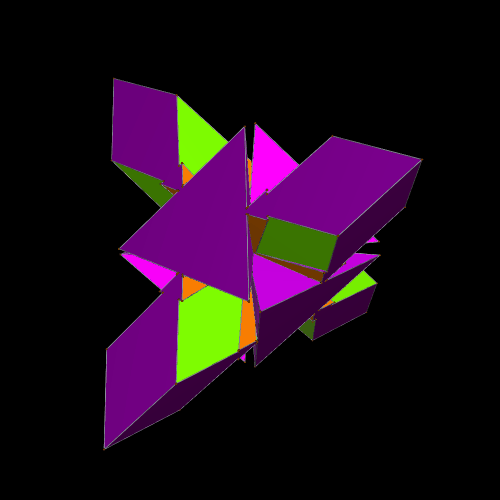
My next step was to create the dual of this polyhedron.
This seemed like a good place to stop, and so I did.
If one starts with a central truncated octahedron, leaves its six square faces untouched, and augments its eight hexagonal faces with trianglular cupolae, this is the result.
Seeing this, I did a quick check of its dual, and found it quite interesting:
After seeing this dual, I next created its convex hull.
After seeing this convex hull, I next creating its dual: one of several 48-faced polyhedra I have found with two different sets of twenty-four kites as faces, one set in six panels of four kites each, and the other set consisting of eight sets of three kites each. I think of these recurring 48-kite-faced polyhedra as polyhedral expressions of a simple fact of arithmetic: (6)(4) = (8)(3) = 24.
I use Stella 4d (available at http://www.software3d.com/Stella.php) to perform these polyhedral transformations. The last one I created in this particular “polyhedral journey” is shown below — but, unfortunately, I cannot recall exactly what I did, to which of the above polyhedra, to create it.
The dual of the icosahedron is the dodecahedron, and a compound can be made of those two solids. If one then takes the convex hull of this solid, the result is a rhombic triacontahedron. One can then made a compound of the rhombic triacontahedron and its dual, the icosidodecahedron — and then take the convex hull of that compound. If one then makes another compound of that convex hull and its dual, and then makes a convex hull of that compound, the dual of this latest convex hull is the polyhedron you see above.
I did try to make the faces of this solid regular, but that attempt did not succeed.
All of these polyhedral manipulations were were performed with Stella 4d: Polyhedron Navigator, available at http://www.software3d.com/Stella.php.
It would really be a pain to count the faces of this polyhedron, in order to verify that there are 270 of them. Fortunately, it isn’t necessary to do so. The polyhedron above is made of rhombus-shaped panels which correspond to the thirty faces of the rhombic triacontahedron. Each of these panels contains nine faces: one square, surrounded by eight triangles. Since (9)(30) = 270, it is therefore possible to see that this polyehdron has 270 faces, without actually going to the trouble to count them, one at a time.
The software I used to make this polyhedron may be found at http://www.software3d.com/Stella.php, and is called Stella 4d. With Stella 4d, a single mouse-click will let you see the dual of a polyhedron. Here’s the dual of the one above.
This polyhedron is unusual, in that it has faces with nine sides (enneagons, or nonagons), as well as fifteen sides (pentadecagons). However, these enneagons and pentadecagons aren’t regular — yet — but they will be in the next post.
One of the thirteen rhombic dodecahedra in this cluster cannot be seen, for it is hidden in the middle. The other twelve are each attached to a face of the central rhombic dodecahedron.
If one then creates the convex hull of this cluster — the smallest convex polyhedron which can contain it — this is the result:
This polyhedron has fifty faces: the six square faces of a cube, the eight triangular faces of an octahedron, the twelve rhombic faces of a rhombic dodecahedron, and twenty-four rectangles to fill the gaps between the other faces.
This fifty-faced polyhedron also has an interesting dual, with 48 faces, all of which are kites. Half of these 48 kites are of one type, and arranged into eight panels of three kites each, while the other half are arranged into six panels of four kites each:
Returning to the fifty-faced polyhedron, two images above, here is what happens if one tries to make each face as regular as possible:
In this polyhedron, the six squares are still squares, the eight triangles are still regular, and the twelve rhombi are still rhombi, although these rhombi are wider than before. The 24 rectangles, however, have now been transformed into isosceles trapezoids.
[Software credit: see http://www.software3d.com/Stella.php for more information about Stella 4d, the program I use to make these rotating images. A free trial download is available at that website.]
RobertLovesPi.net 