Is It Moving?

Posted on 14 January 2015 by RobertLovesPi

Creating a Faceting of the Truncated Icosahedron

Posted on 13 January 2015 by RobertLovesPi

To make a faceted polyhedron, vertices of the original polyhedron are connected in new ways, to create a different set of faces and edges. To make this particular faceting of the truncated icosahedron, I first connected all vertices in the configuration shown below, to make irregular decagonal faces in the interior of the solid.

In this next pic, the decagonal faces formed above are shown in red, and a new set of pentagonal faces is being created.

For a polyhedron to be considered mathematically valid, faces must meet in pairs at each edge. To accomplish that, I had to create another set of pentagonal faces, this one smaller than the last, as shown below.

Here’s the completed polyhedron, with each face-type having its own color.

This next image is of the same polyhedron, but with a different coloring-scheme. In this second version, each face has its own color — except for faces which are parallel, with those faces given the fame color.

I created these images using Stella 4d: Polyhedron Navigator, a program which is available here.

At 47, My Age Is a Prime Number Again =D

Posted on 12 January 2015 by RobertLovesPi

For some reason, I like having my age be a prime number of years. Today, I turn 47, so I get to have a prime-number-age for a whole year now. This hasn’t happened since I was 43, so I made this 47-pointed star to celebrate:

I also make birthday-stars for composite-number ages as well, just because it’s fun, and you can find at least two others on this blog, on January 12, in past years. Also, I wouldn’t want to have to wait until I’m 53 (my next prime age) to make another one of these.

At the moment, I certainly don’t feel 47. There are times when I feel twenty-two . . .

There are also times when I feel six.

At the moment, however, I feel about thirty. For that reason, I put the 47-pointed stars on the thirty faces of a rotating rhombic triacontahedron, because (a) it’s my birthday, (b) I want to, and (c) I can.

Image/music credits:

I created this using Geometer’s Sketchpad and MS-Paint.
“When Yer Twenty-Two,” by The Flaming Lips, via a YouTube posting.
Two panels from a Calvin and Hobbes cartoon, by Bill Watterson. (Calvin is perpetually six years old.)
Created using the image at the top of this post, and the program Stella 4d: Polyhedron Navigator, which is available here.

My First Solution to the Zome Cryptocube Puzzle, with Special Guest Appearances by Jynx the Kitten

Posted on 11 January 2015 by RobertLovesPi

Last month, in a special Christmas promotion, the Zometool company (www.zometool.com) briefly sold a new kit (which will return later) — a fascinating game, or puzzle, called the “Cryptocube.” Zome usually comes in a variety of colors, with each color having mathematical significance, but the Cryptocube is produced in black and white, which actually (in my opinion) makes it a better puzzle. Here’s how the Crypocube challenge works: you use the black parts to make a simple cube, and then use the smaller white parts to invent a structure which incorporates the cube, is symmetrical, is attractive, and can survive having the twelve black cube-edges removed, leaving only the cube’s eight black vertices in place. I had a lot of fun making my first Cryptocube, and photographed it from several angles.

If this was built using standard Zome colors, the round white figure inside the cube, a rhombic triacontahedron, would be red, and the pieces outside the cube, as well as those joining the rhombic triacontahedron to the cube (from inside the cube), would be yellow.

It isn’t only humans who like Zome, by the way. Jynx the Kitten had to get in on this!

Jynx quickly became distracted from the Cryptocube by another puzzle, though: he wanted to figure out how to pull down the red sheet I had attached to the wall, as a photographic backdrop for the Cryptocube. Jynx takes his feline duties as an agent of entropy quite seriously.

As usually happens, Jynx won (in his never-ending struggle to interfere with whatever I’m doing, in this case by pulling the sheet down) and it took me quite a while to get the red sheet back up, in order to take kitten-free pictures of my Cryptocube solution, after removal of the black cube’s edges.

Here’s the view from another angle.

The Cryptocube will be back, available on the Zometool website, later in 2015. In the meantime, I have advice for anyone not yet familiar with Zome, but who wants to try the Cryptocube when it returns: go ahead and get some Zome now, at the link above, in the standard colors (red, blue, and yellow, plus green in advanced kits), and have fun building things with it over the next few months. The reason to do this, before attempting to solve the Crypocube, is simple: the colors help you learn how the Zome system works, which is important before trying to solve a Zome puzzle without these colors visible. After gaining some familiarity with the differing shapes of the red, blue, yellow, and green pieces, working with them in white becomes much easier.

On a related note, Zome was recommended by Time magazine, using the words “Zometool will make your kids smarter,” as one of the 14 best toys of 2013. I give Zome my own strong, personal recommendation as well, and, as a teacher who uses my own Zome collection in class, for instructional purposes, I can attest that Time‘s 2013 statement about Zome is absolutely correct. Zome is definitely a winner!

On the Possible Numbers of Vertices of Extended Convex Polygons

Posted on 10 January 2015 by RobertLovesPi

A few days ago, I came across the phrase, while surfing the Internet, “the extended quadrilateral has six vertices.” Not understanding this, I researched the matter, and found out what this phrase means. If the normal four vertices of a quadrilateral are placed such that the quadrilateral has no parallel sides, then two additional vertices are created when the four sides are extended as lines, as shown below. This gives a total of six vertices for this extended quadrilateral.

Of course, one need not position the vertices in this way. Trapezoids, by definition, have one pair of parallel sides. The non-parallel sides of an extended trapezoid still intersect outside this quadrilateral, creating a five-vertex situation.

The other option is the parallelogram, with two pairs of parallel sides. This eliminates additional vertices altogether, so there are only four.

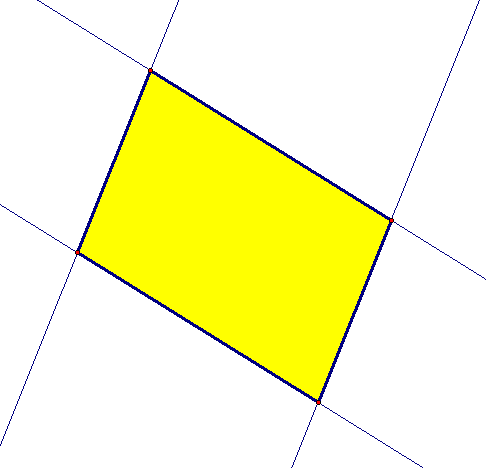
This exhausts the possibilities, so the possible numbers of vertices for extended quadrilaterals are 4, 5, and 6.

Realizing this, of course, just raises other questions: what about other extended convex polygons? What are the numbers of possible intersections for such polygons with varying numbers of sides? Is there a pattern? To investigate this, I needed data, and started by taking a step back from quadrilaterals, to briefly consider extended triangles.

Extending the sides of any triangle creates no additional vertices, beyond the three which exist before the extension. This is a result of the fact that three is the maximum number of intersections created by three coplanar lines. Three is, therefore, for triangles, the only answer.

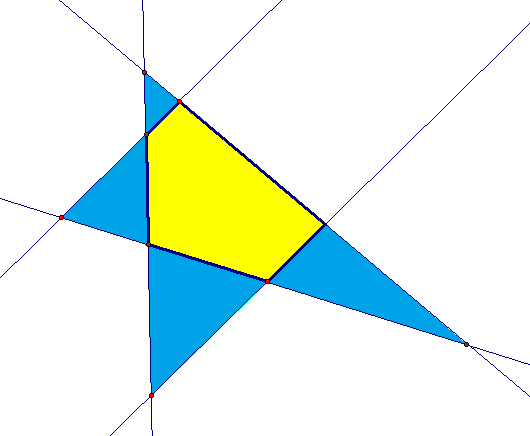
The next step: consider extended convex pentagons. I decided to start by maximizing the number of vertices, by having no parallel sides at all.

As you can see above, this produces ten vertices — five for the non-entended pentagon, plus five more formed by the entensions. To reduce this number, I simply moved vertices of the original, non-extended pentagon to eliminate external vertices, one at a time, by creating pairs of parallel sides.

With one pair of parallel sides, as shown above, the number of vertices is reduced by one, from ten to nine.

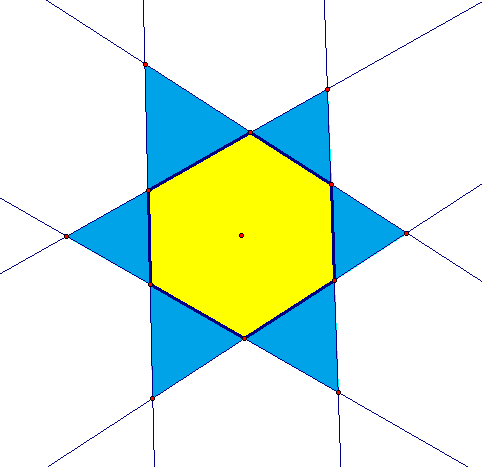
For pentagons, the maximum number of pairs of parallel sides is two, as shown above, which lowers the total number of vertices to eight. For pentagons, then, there are three solutions to this puzzle: 8, 9, and 10.

Next, I considered hexagons.

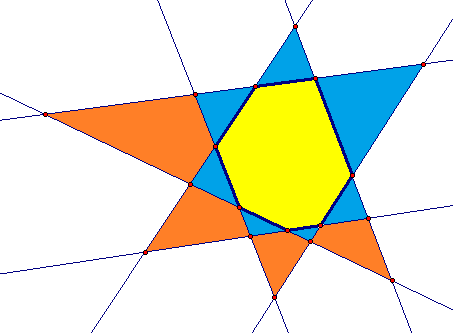
The extended hexagon above has no parallel sides, which gives it the maximum number of vertices: fifteen. In the figure below, by contrast, there is one pair of parallel sides, reducing this number to fourteen.

With two pairs of parallel sides, as shown above, this number again decreases by one, to thirteen. Three pairs of parallel sides is the maximum for hexagons, and is shown below; for this extended hexagon, there are twelve vertices.

For hexagons, then, there are four solutions: 15, 14, 13, and 12.

Still needing more data, I next investigated extended convex heptagons. With no parallel sides at all, as shown below, the total number of vertices is twenty-one.

If only one pair of parallel sides exist, there is one less vertex than the previous answer gave, and this number is twenty, as shown above. It is also possible for there to be two pairs of parallel sides, as shown below, and this yields nineteen vertices.

For heptagons, there is only one other option: three pairs of parallel sides. (A fourth pair would require eight sides.) This situation is shown below, and in it, there are eighteen vertices.

For heptagons, then, the solutions are four in number: 18, 19, 20, and 21.

Next: octagons. With no sides parallel, to obtain the maximum number of vertices (as shown below), there are twenty-eight of them.

In the diagram below, the solution immediately above is reduced by one, to twenty-seven, by making one pair of sides parallel.

The next solution is shown below, and is twenty-six. This is accomplished by making two pair of sides parallel.

To obtain twenty-five vertices, three pairs of sides are made to be parallel, as shown below.

Finally, twenty-four vertices, the minimum for octagons, requires all four pairs of opposite sides to be parallel. This solution is shown below.

Octagons, then, have five solutions: 24 to 28, inclusive.

Here is the data gathered above, in the form of a table, along with additional data obtained by extrapolation, work shown toward a generalized solution, and then that generalized solution itself, in three parts: one for triangles, one where the number of sides is even, and one where n, the number of sides, is odd, with n > 3.

The Final Stellation of the Icosahedron

Posted on 9 January 2015 by RobertLovesPi

This is what you get if you stellate an icosahedron seventeen times. The eighteenth stellation “loops” back around to the original figure, the icosahedron. For this reason, the figure above is often called “the final stellation of the icosahedron,” as well as “the complete icosahedron.” Its faces are twenty irregular star enneagons, of the type shown below. The red areas are the “facelets” which can be seen, while the other parts of the star enneagon are hidden inside the figure.

Both of these images were made using Stella 4d: Polyhedron Navigator, which you can try for yourself right here. A free trial download is available.

Green Icosidodecahedral Cage

Posted on 8 January 2015 by RobertLovesPi

In this icosidodecahedron, the pentagonal faces have been removed, and the triangular faces have been augmented with short pyramids. I used Stella 4d to make it, which you can find here.

An 1800-Faced Polyhedron, with Its 960-Faced Dual

Posted on 7 January 2015 by RobertLovesPi

The polyhedra shown above and below are duals. The one above has 1800 faces and 960 vertices. The one below has 960 faces, and 1800 vertices. This “flipping” of the face and vertex numbers always happens with dual polyhedra.

Also, two dual polyhedra always have the same number of edges, which can be found by subtracting two from the sum of the numbers of faces and vertices (this is based on Euler’s Formula, F + V = E + 2). In this case, each of these polyhedra have 1800 + 960 – 2 = 2758 edges.

These virtual models were created using Stella 4d: Polyhedron Navigator, software you can try for yourself right here.

[Later note: I have noticed a lot of referrals to this post through stumbleupon.com, and wish to thank the unknown person who posted the link there for all this increased traffic to my blog. To those who are finding me via StumbleUpon, welcome! I invite you to check out other posts here, as well. The “topic cloud” on the right side of the page should help you find stuff of interest to you, of the 1000+ posts here, many of which are also about polyhedra.]

A Polyhedron with Eight Regular Hexagonal Faces and Twenty-Four Irregular Pentagonal Faces

Posted on 6 January 2015 by RobertLovesPi

There are many polyhedra that include only hexagons and pentagons as faces — infinitely many, in fact. Most of the well-studied ones include twelve regular pentagonal faces, though, but this polyhedron has twenty-four pentagons, none of which are regular, in six panels of four pentagons each. Its regular faces are the eight hexagons, in the face-planes of the faces of an octahedron.

I made this with Stella 4d, software you can try here.

The WM Function

Posted on 3 January 2015 by RobertLovesPi

As if the world needed another trigonometric function, I give it the WM function, named after the letters apparent in its graph. It is the sine of the sine of x, times 2π, if x is measured in radians, as in the graph below.