Halving and Rehalving, as Well as Doubling and Redoubling, as a Calculator-Free Calculating Strategy

Posted on 21 January 2015 by RobertLovesPi

I don’t like being too dependent on calculators. The future might bring an EMP (electromagnetic pulse) that would fry all such gadgets (and cell phones, cars, computers, etc.), and I want to be ready for a post-calculator world, if that happens.

My overarching strategy for doing math in my head is this: don’t have just one single strategy. Instead, devise one, on the fly, based on the problem you are trying to solve.

I do, however, use a few “go to” strategies for certain things, such as finding 25% of something, or multiplying by eight, or similar problems. This involves looking for, and take advantage of, powers of two, as well as their reciprocals. 25% is 1/4, which is simply halving twice, and multiplying by eight is three doublings, since 8 = 2³. With practice, doubling or halving numbers repeatedly and silently, in one’s head, becomes much faster and easier. If done out loud, it becomes easier still, and on paper, it’s extremely easy.

I intend to do more blog-posts in the future with calculator-free calculation strategies, but not all at once — instead, these techniques will be posted one at a time. However, these postings will stop immediately, in the event of an EMP.

My First Solution to the Zome Cryptocube Puzzle, with Special Guest Appearances by Jynx the Kitten

Posted on 11 January 2015 by RobertLovesPi

Last month, in a special Christmas promotion, the Zometool company (www.zometool.com) briefly sold a new kit (which will return later) — a fascinating game, or puzzle, called the “Cryptocube.” Zome usually comes in a variety of colors, with each color having mathematical significance, but the Cryptocube is produced in black and white, which actually (in my opinion) makes it a better puzzle. Here’s how the Crypocube challenge works: you use the black parts to make a simple cube, and then use the smaller white parts to invent a structure which incorporates the cube, is symmetrical, is attractive, and can survive having the twelve black cube-edges removed, leaving only the cube’s eight black vertices in place. I had a lot of fun making my first Cryptocube, and photographed it from several angles.

If this was built using standard Zome colors, the round white figure inside the cube, a rhombic triacontahedron, would be red, and the pieces outside the cube, as well as those joining the rhombic triacontahedron to the cube (from inside the cube), would be yellow.

It isn’t only humans who like Zome, by the way. Jynx the Kitten had to get in on this!

Jynx quickly became distracted from the Cryptocube by another puzzle, though: he wanted to figure out how to pull down the red sheet I had attached to the wall, as a photographic backdrop for the Cryptocube. Jynx takes his feline duties as an agent of entropy quite seriously.

As usually happens, Jynx won (in his never-ending struggle to interfere with whatever I’m doing, in this case by pulling the sheet down) and it took me quite a while to get the red sheet back up, in order to take kitten-free pictures of my Cryptocube solution, after removal of the black cube’s edges.

Here’s the view from another angle.

The Cryptocube will be back, available on the Zometool website, later in 2015. In the meantime, I have advice for anyone not yet familiar with Zome, but who wants to try the Cryptocube when it returns: go ahead and get some Zome now, at the link above, in the standard colors (red, blue, and yellow, plus green in advanced kits), and have fun building things with it over the next few months. The reason to do this, before attempting to solve the Crypocube, is simple: the colors help you learn how the Zome system works, which is important before trying to solve a Zome puzzle without these colors visible. After gaining some familiarity with the differing shapes of the red, blue, yellow, and green pieces, working with them in white becomes much easier.

On a related note, Zome was recommended by Time magazine, using the words “Zometool will make your kids smarter,” as one of the 14 best toys of 2013. I give Zome my own strong, personal recommendation as well, and, as a teacher who uses my own Zome collection in class, for instructional purposes, I can attest that Time‘s 2013 statement about Zome is absolutely correct. Zome is definitely a winner!

A Special Type of Compound, Built with Zome, of the Great and Small Stellated Dodecahedra

Posted on 17 December 2014 by RobertLovesPi

For years, I have used Zometools (sold here: http://www.zometool.com) to teach geometry. The constructions for the icosahedron and dodecahedron are easy to teach and learn, due to the use of short reds (R1s) and medium yellows (Y2s) for radii for the two of them, as shown below, with short blue (B1) struts as edges for both polyhedra.

Unexpectedly, a student (name withheld for ethical and legal reasons) combined the two models, making this:

I saw it, and wondered if the two combined Platonic solids could be expanded along the edges, to stellate both polyhedra, with medium blues (B2s), to form the great and small stellated dodecahedron. By trying it, I found out that this would require intersecting blue struts — so a Zomeball needed to be there, at the intersection. Trying, however, only told me that no available combination would fit. After several more attempts, I doubled each edge length, and added some stabilizing tiny reds (R0s), and found a combination that would work, to form a compound of the great and small stellated dodecahedron in which both edge lengths would be equal. In the standard (non-stellated) compound of the icosahedron and dodecahedron, in which the edges are perpendicular, they are unequal in length, and in the golden ratio, which is how that compound differs from the figure shown directly above.

Here’s the stabilized icosahedral core, after the doubling of the edge length:

This enabled stellation of each shape by edge-extension. Each edge had a length twice as long as a B2 added to each side — and it turns out, I discovered, that 2B2 in Zome equals B3 + B0, giving the golden ratio as one of three solutions solution to x² + 1/x = 2x (the others are one, and the golden ratio’s reciprocal). After edge-stellation to each component of the icosahedron/dodecahedron quasi-compound, this is what the end product looked like. This required assembling the model below at home, where all these pictures were taken, for one simple reason: this thing is too wide to fit through the door of my classroom, or into my car.

Here’s a close-up of the central region, as well.

On Triangle Congruence, and Why SSA Does Not Work

Posted on 18 November 2014 by RobertLovesPi

Those who have taught geometry, when teaching triangle congruence, go through a familiar pattern. SSS (side-side-side) triangle congruence is usually taught first, as a postulate, or axiom — a statement so obvious that it requires no proof (although demonstrations certainly do help students understand such statements, even if rigorous proof is not possible). Next, SAS (side-angle-side) and ASA (angle-side-angle) congruence are taught, and most textbooks also present them as postulates. AAS (angle-angle-side) congruence is different, however, for it need not be presented without proof, for it follows logically from ASA congruence, paired with the Triangle Sum Theorem. With such a proof, of course, AAS can be called a theorem — and one of the goals of geometricians is to keep the number of postulates as low as possible, for we dislike asking people to simply accept something, without proof.

At about this point in a geometry course, because the subject usually is taught to teenagers, some student, to an audience of giggling and/or snickering, will usually ask something like, “When are we going to learn about angle-side-side?”

The simple answer, of course, is that there’s no such thing, but there’s a much better reason for this than simple avoidance of an acronym which many teenagers, being teenagers, find amusing. When I’ve been asked this question (and, yes, it has come up, every time I have taught geometry), I accept it as a valid question — since, after all, it is — and then proceed to answer it. The first step is to announce that, for the sake of decorum, we’ll call it SSA (side-side-angle), rather than using a synonym for a donkey (in all caps, no less), by spelling the acronym in the other direction. Having set aside the silliness, we can then tackle the actual, valid question: why does SSA not work?

This actually is a question worth spending class time on, for it goes to the heart of what conjectures, theorems, proof, and disproof by counterexample actually mean. When I deal with SSA in class, I refer to it, first, as a conjecture: that two triangles can be shown to be congruent if they each contain two pairs of corresponding, congruent sides, and a pair of corresponding and congruent angles which are not included between the congruent sides, of either triangle. To turn a conjecture into a theorem requires rigorous proof, but, if a conjecture is false, only one counterexample is needed to disprove its validity. Having explained that, I provide this counterexample, to show why SSA does not work:

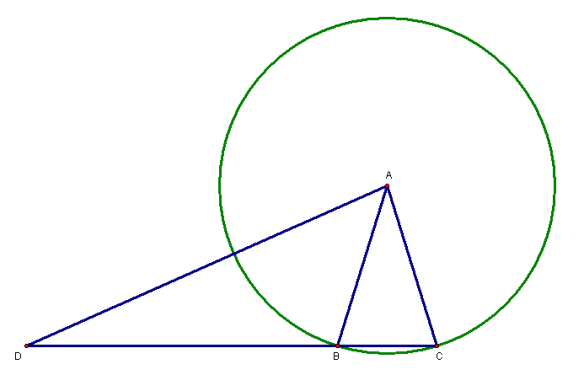
In this figure, A is at the center of the green circle. Since segments AB and AC are radii of the same circle, those two segments must be congruent to each other. Also, since congruence of segments is reflexive, segment AD must be congruent to itself — and, finally, because angle congruence is also reflexive, angle D must also be congruent to itself.

That’s two pairs of corresponding and congruent segments, plus a non-included pair of congruent and corresponding angles, in triangle ABD, as well as triangle ACD. If SSA congruence worked, therefore, we could use it to prove that triangle ABD and triangle ACD are congruent, when, clearly, they are not. Triangle ACD contains all the points inside triangle ABD, plus others found in isosceles triangle ABC, so triangles ABD and ACD are thereby shown to have different sizes — and, by this point, it has already been explained that two triangles are congruent if, and only if, they have the same size and shape. This single counterexample proves that SSA does not work.

Now, can this figure be modified, to produce an argument for a different type of triangle congruence? Yes, it can. All that is needed is to add the altitude to the base of isosceles triangle ABC, and name the foot of that altitude point E, thereby creating right triangle AED.

It turns out that, for right triangles only, SSA actually does work! The relevant parts of the right triangle, shown in red, are segment DA (congruent to itself, in any figure set up this way), segment AE (also congruent to itself), and the right angle AED (since all right angles are congruent to each other). However, as I’ve explained to students many times, we don’t call this SSA congruence, since SSA only works for right triangles. To call this form of triangle congruence SSA (forwards or backwards), when it only works for some triangles, would be confusing. We use, instead, terms that are specific to right triangles — and that’s how I introduce HL (hypotenuse-leg) congruence, which is what SSA congruence for right triangles is called, in order to avoid confusion. Only right triangles, of course, contain a hypotenuse.

This is simply one example of how to use a potentially-disruptive student question — also known as a teenager being silly — and turn it around, using it as an opportunity to teach something. Many other examples exist, of course, in multiple fields of learning.

Kaizen

Posted on 1 November 2014 by RobertLovesPi

I painted this many years ago, as a classroom poster, and then moved it from classroom to classroom, for years, until the posterboard on which it was painted was finally too damaged for further use. At some point, I will have to make a replacement.

Kaizen is a Japanese word which translates only loosely into English, as “continuous improvement.” To me, it means more than that: it means never being content with simply staying the person I am today, and going to sleep, each night, with the sincere intention to be a better person tomorrow.

Does this always actually work, as each day becomes the next one? No, I must admit that it doesn’t — but that does nothing to change the fact that keeping the kaizen principle in mind is an excellent way to live one’s life. On a year-to-year basis, it works much better, in practice, than it does from day to day. I am confident that I am a better person now than I was 365 days ago, even though there have, of course, been ups and downs, as the last year has passed.

Setbacks, which happen to everyone, are no reason to give up, and personal improvement, in all important parts of life, will always be a goal worth pursuing.

“How Tall Are You?”

Posted on 12 October 2014 by RobertLovesPi

When I am asked for my height, anywhere — especially at school — I answer the question honestly. I am 1.80 meters tall.

I also live in the USA, one of only three remaining countries (the other two holdouts are Liberia and Myanmar) which have stubbornly refused to adopt the metric system. However, I am every bit as stubborn as other Americans, but, on this issue, I choose to be stubborn in the opposite direction.

It should surprise no one who knows me well that my classroom, whether I am teaching science or mathematics, is, by design, an all-metric zone. After all, like >99% of people, I have ten fingers (assuming thumbs are counted as fingers), ten toes, and almost always use the familiar base-ten number system when counting, measuring, doing arithmetic, or doing actual mathematics. (Doing arithmetic is not the same thing as doing real mathematics, any more than spelling is equivalent to writing.) Using the metric system is consistent with these facts, and using other units is not.

Admittedly, I do sometimes carry this to an extreme, but I do so to make a point. Metric units are simply better than non-metric units. Why should anyone need to memorize the fact that there are 5,280 feet in one mile? It actually embarrasses me that I have that particular conversion-factor memorized. By “extreme,” I mean that I have been known to paint the non-metric side of meter sticks black, simply to make it impossible for students in my classes to confuse inches and centimeters, and prevent them from measuring anything with the incorrect units.

To those who object that American students need to understand non-metric units, I simply point out that there are plenty of other teachers who take care of that. This is, after all, the truth.

Often, after giving my height as 1.80 meters, I am asked to give it in other units. Unless the person asking is a police officer (in, say, a traffic-stop situation), however, I simply refuse to answer with non-metric units. What do I say, instead? “I’m also 180 centimeters tall. Would you like to know my height in kilometers?”

If pressed on this subject in class — and it comes up, because we do lab exercises where the height of people must be measured — I will go exactly this far: I am willing to tell a curious student that there are 2.54 centimeters in an inch, 12 inches in a foot, and 3.28 feet in a meter. Also, I’m willing to loan calculators to students. Beyond that, if a student of mine really wants to know my height in non-metric units, he or she simply has to solve the problem for themselves — something which has not yet happened. I do not wish to tell anyone my height in feet and inches, for I do not enjoy headaches, and uttering my height, in those units I despise, would certainly give me one. Also, obviously, you won’t find my height, expressed in non-metric units, on my blog, unless someone else leaves it here, in a comment — and I am definitely not asking anyone to do that.

I might, just for fun, at some point, determine my height in cubits. For all I know, a person’s height, measured with their own cubits, might be a near-constant. That would be an interesting thing to investigate, and my students, now that I’ve thought about the question, might find themselves investigating this very issue, next week. The variability of cubits, from one person to another, makes them at least somewhat interesting. It also makes cubits almost completely useless, which explains why they haven’t been used since biblical times, but that’s not the point. One can still learn things while investigating something which is useless, if one is sufficiently clever about it.

Feet and inches, however, are not interesting — at all. They are obsolete, just as cubits are, and they are also . . . offensive. It is not a good thing to insult one’s own brain.

My Aqua Regia Story

Posted on 6 October 2014 by RobertLovesPi

This is my twentieth year teaching, but only the first year when I have not taught at least one class in chemistry, and I miss it. One of my fondest memories of chemistry lab involves the one time I experimented with aqua regia — a mixture of acids which, unlike any single acid, can dissolve both gold and platinum, the “noble metals.” I had read a story of a scientist’s gold Nobel Prize being protected from the Nazis by dissolving it in aqua regia, and then recovering the gold from solution after World War II had ended. Having read about this, I wanted to try it myself, and also thought it would make an excellent lab for classroom use — if I could figure out how to recover the gold, and also learn what precautions would be needed to allow high school students to perform this experiment safely. For sensible and obvious reasons, I conducted a “trial run” without students present, but with another chemistry teacher nearby, since aqua regia, and the gases it produces when dissolving gold, are quite dangerous. Someone else has put a video on YouTube, showing aqua regia dissolving gold, so you can see something much like what I saw, simply by watching this video.

First, I obtained one-tenth of a troy ounce of gold, which cost about $80 at the time. I had read about the extreme malleability of gold, one of the softest metals, and wanted to see evidence for it for myself — so, before I prepared the the aqua regia, I used a hammer to try flattening the gold sample into a thin sheet. That didn’t work, but it didn’t take long for me to figure out why — I had accidentally bought gold coin-alloy, which is 10% copper, not pure gold. Since this alloy is far less malleable than pure gold, my attempt to flatten it had failed, but I also knew this would not pose a problem for my primary experiment — the one involving aqua regia. Also, I didn’t have another spare $80 handy, to purchase another 1/10 troy ounce of pure gold, so I proceeded to make, for the first time in my life, a small amount of aqua regia — Latin for “royal water.”

Unlike what is shown in the video above, I prepared the acid-mixture first, before adding the gold, using a slightly-different recipe: the traditional 1:4 ratio, by volume, of concentrated nitric acid to concentrated hydrochloric acid. Both these acids look (superficially) like water, but the mixture instantly turned yellow, and started fuming, even before anything was added to it. Wearing full protective gear, I watched it for a few minutes — and then, using tongs held by gloved hands, lowered my hammer-bashed sample of gold into the fuming, yellow mixture of concentrated acids.

It worked. It was a fascinating reaction, and a lot of fun to watch. At approximately the same time that the last of my gold sample dissolved, something occurred to me: I had failed to research how to recover the dissolved gold from the resulting solution! No problem, I thought — I can figure this out. (I am seldom accused of lacking self-confidence, even when I’m wrong.)

My first idea was to use a single-replacement reaction. Many times, I have had students extract pure silver from a solution of silver nitrate by adding a more-active metal, such as copper. The copper dissolves, replacing the silver in the silver nitrate solution, and silver powder forms, as a precipitate, on the surface of the copper. Thinking that a similar process could be used to precipitate out the gold from my gold / aqua regia mixure, I simply added come copper to the reaction beaker. The corrosive properties of my aqua regia sample had not yet been exhausted, though, and so the remaining aqua regia simply “ate” the copper. The result was a mess — I had only succeeded in turning an already-complicated problem into an even-more-complicated problem, by adding more chemicals to the mixture. More attempts to turn the gold ions back into solid gold dust, using other chemicals, followed, but all of them failed. Finally, I used a strong base, sodium hydroxide, to neutralize the still-acidic mixture, and then, disgusted by my failure to recover the gold, found a way to safely dispose of the mixture, and did so.

In retrospect, I think I know where I messed up — I should have neutralized the remaining acids in the mixture with sodium hydroxide first, before adding copper to cause the gold to precipitate out, in a no-longer-acidic solution of ions with much less hydronium present. That, I think, will work, and I do intend to try it sometime — after doing more research first, to increase my level of certainty, and also after waiting for the current price of gold to drop to less-expensive levels. Right now, after all, a tenth of a troy ounce of gold costs roughly $120, not a mere $80.

As for the lost $80, I’m not upset about that anymore. I definitely learned things while doing this, and now view the $80 spent as simply the cost of tuition for an educational experience.

Zome: Strut-Length Chart and Product Review

Posted on 22 September 2014 by RobertLovesPi

This chart shows strut-lengths for all the Zomestruts available here (http://www.zometool.com/bulk-parts/), as well as the now-discontinued (and therefore shaded differently) B3, Y3, and R3 struts, which are still found in older Zome collections, such as my own, which has been at least 14 years in the making.

In my opinion, the best buy on the Zome website that’s under $200 is the “Hyperdo” kit, at http://www.zometool.com/the-hyperdo/, and the main page for the Zome company’s website is http://www.zometool.com/. I know of no other physical modeling system, both in mathematics and several sciences, which exceeds Zome — in either quality or usefulness. I’ve used it in the classroom, with great success, for many years.

The Eleven Oddball Symbols on the Periodic Table of the Elements

Posted on 20 September 2014 by RobertLovesPi

Most symbols for elements on the periodic table are easy to learn, such as those for carbon, oxygen, and nitrogen: C, O, and N. There are eleven “oddballs,” though, because their symbols originated in other languages (Latin, mostly), and do not match their English names. Here’s a list of them, by atomic number, with an explanation for each.

11. Na stands for sodium because this element used to be called natrium.

19. K stands for potassium, for this element’s name used to be kalium.

26. Fe stands for iron because this element was formerly named ferrum.

29. Cu stands for copper because it used to be called cuprum.

47. Ag’s (silver’s) old name was argentum.

50. Sn’s (tin’s) name used to be stannum.

51. Antimony’s symbol, Sb, came from its former name, stibium.

74. Tungsten, with the symbol W, was once called wolfram. In some parts of the world, it still goes by that name, in fact.

79. Gold (Au) was called aurum in past centuries.

80. Mercury’s (Hg’s) old name is impossible (for me, anyway) to say five times, quickly: hydrargyrum.

82. Lead (Pb) was once called plumbum because plumbers used it to weight the lower end of plumb-lines.

I think learning things is easier, with longer retention, if one knows the reasons behind the facts, rather than simply attempting rote memorization.

My Australia Story

Posted on 10 September 2014 by RobertLovesPi

I once got into a huge argument, as a 7th grade student, in a “talented and gifted” section of Social Studies. The issue: how many countries are there in the continent of Australia?

The assignment was to choose a continent, and draw a map of it on a full-size posterboard. I had worked for hours on this map, only to get it back, ruined, for the teacher had taken a red ball-point pen, slashed through my line “state and territorial boundaries” in my map’s key, and had written, as a correction, “not states — COUNTRIES.” She also docked points from my grade, but that was a minor issue, to me, compared to her ruining my map. She could have, at least, written her incorrect comment on the back of my map!

When I confronted her about her mistake, she maintained that the political divisions you see above are independent countries. In my opinion, “Northern Territory,” especially, doesn’t sound particularly sovereign, and I said so, but she may not have understood the definition of “sovereign,” for that did not work. Confronted with this absurd situation, I proceeded to grab the “Q” volume of a nearby encyclopedia, and began reading the article about Queensland, loudly enough for the entire class to hear: “Queensland: one of the states of Australia….” I freely admit that, at the time, my goal was to embarrass and humiliate her right out of the teaching profession — for the benefit of her present and future students. I’ve changed my approach, a lot, since then.

A huge brouhaha ensued, and we ended up taking each other to the assistant principal’s office: her, to report a disruptive and defiant student; and me, to report an incompetent teacher, who, in my view, at that age, should have been fired on the spot. Dealing with this situation was probably one of the stranger, and more difficult, situations of that assistant principal’s career, for he knew that Australia is both a single country, and a continent — but he could not, for political reasons I did not yet understand, agree with me in front of this teacher. As for me, I was simply incredulous that someone could be a certified social studies teacher, and not know this basic fact about world geography. The whole scenario, to me, was surreal.

The assistant principal handled it well. To the teacher, he said, “You can go back to class — I’ll handle Robert.” He then “handled” me, after she left, in the only way that could have possibly worked: with an apology, and a polite request to do my best to endure her ignorance until the upcoming end of the year. I respect honesty, was being given a request, not an order, and he had conceded that I was correct. I therefore chose to cooperate — with his polite request.

If he had not taken this approach, I likely would have added him to the list I had, at the time, of people (a mixture of administrators and teachers) whom I was trying to drive out of the education profession, for the benefit of all — but he did the right thing, thus earning my respect.

As for the teacher, I survived the rest of her class, brain intact, and assume she is now retired, this being well over thirty years ago. I’m now in my twentieth year as a teacher, myself, and am pleased to report that average teacher quality has dramatically improved since this fiasco happened. (I wish I could say the same about average administrator quality, but there are, at least, a few competent people working in that field, as well.) During my years of teaching, I haven’t encountered a single teacher who lacked this basic bit of knowledge about world geography. In fact, I count, among my colleagues, many of the smartest people I know.

I am glad, however, that I don’t have to call the teacher in this story a colleague. I simply cannot respect willful, stubborn ignorance, especially in the face of evidence that one is wrong. When one of my students catches me making a mistake, I do the right thing: I thank them, make certain everyone understands the correction, and then we move on with the lesson. That’s what this 7th grade teacher of mine should have done, as well.