Pictured above is the most familiar hexagonal tessellation. I’ve found some additional tessellations which use equilateral (but non-equiangular) hexagons, and have radial symmetry. They appear, using various coloring-schemes, below.
When I tweet a link to this blog-post as @robertlovespi, it will likely be quickly retweeted by @hexagonbot, simply because of the term “hexagon” being included in the tweet. What I don’t understand: Why do other polygons not have bots of their own?
I used Stella 4d to make this image, and you can find that program at http://www.software3d.com/Stella.php.
I created this using Stella 4d: Polyhedron Navigator, a program you can find at http://www.software3d.com/Stella.php.
In this chiral tessellation, the blue triangles and green hexagons are regular. The yellow hexagons are “Golden Hexagons,” which are what you get if you reflect a regular pentagon over one of its own diagonals, then unify the two reflections. The pink and purple quadrilaterals are two types of rhombi, and the red hexagons are a third type of equilateral hexagon. All of the edges of all polygons here have the same length.
There are three different types of points of three-fold rotational symmetry repeated here. Two of these types are centered in the middle of blue triangles, while the third is centered in the middle of some of the green hexagons — specifically, the ones surrounded only by alternating red and yellow hexagons.
When I try to generate the mirror-image of this tessellation, it overloads Geometer’s Sketchpad, and crashes the program. However, inverting the colors of the same reflection, in MS-Paint, to make a color-variant, is easy:
If you’d like to see the second version of this tessellation, made over a decade later, simply click right here.
I created this using Stella 4d, which is available (including a free trial download) at http://www.software3d.com/Stella.php. With adjustments in edge lengths to make the bond lengths correct, this would be the shape of a C180 fullerene molecule.
If the thirty-two faces of the truncated icosahedron are hidden, and only the sixty extra hexagons are visible, this polyhedron looks like this:
In “rainbow color mode,” it has an even more interesting appearance:
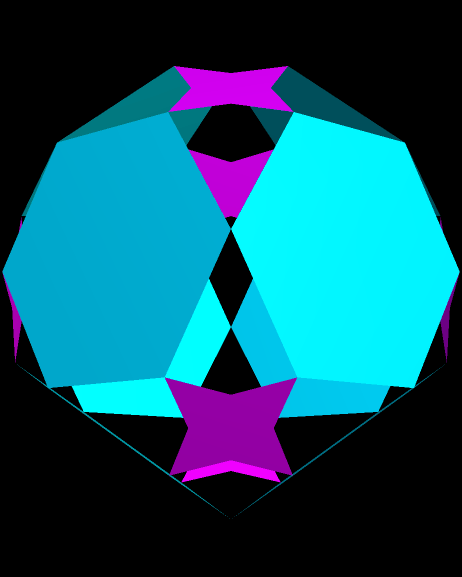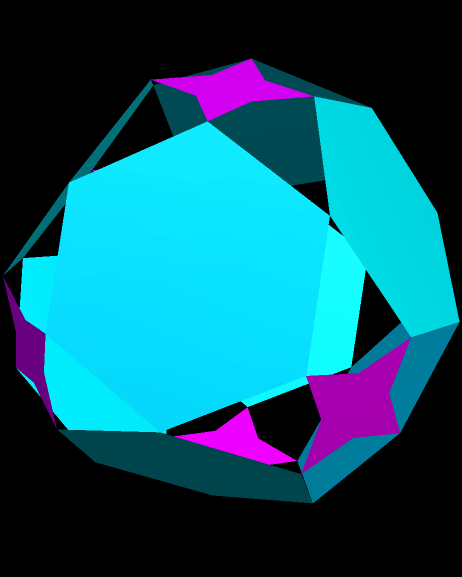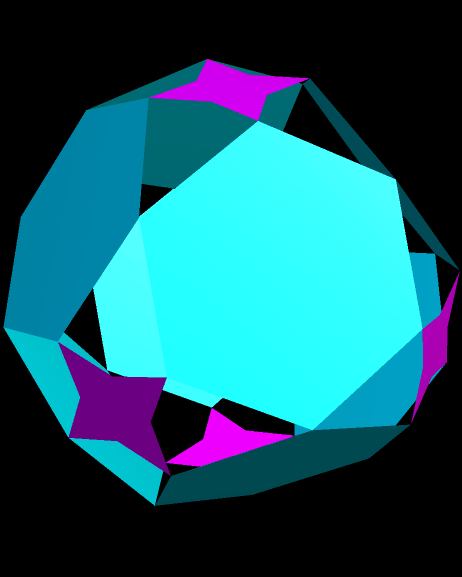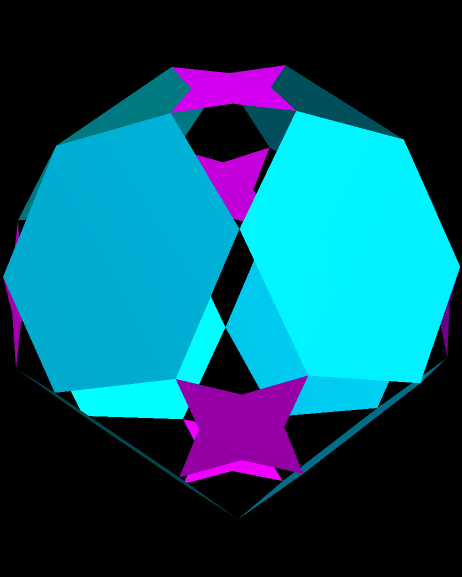
Software credit: see http://www.software3d.com/Stella.php for more information on Stella 4d, the program I used to make this. A free trial download is available.
This image was produced using Stella 4d, which you may try for free, right here: http://www.software3d.com/Stella.php.
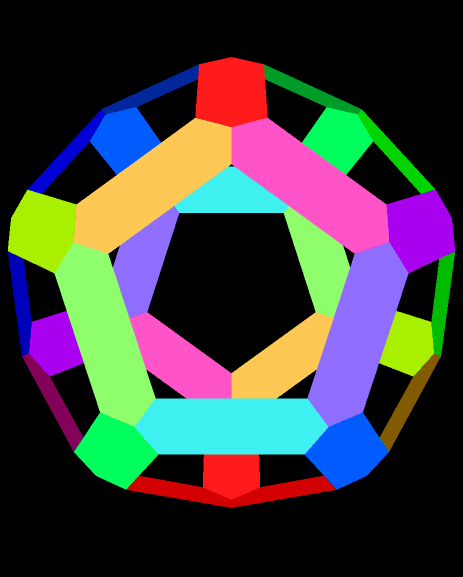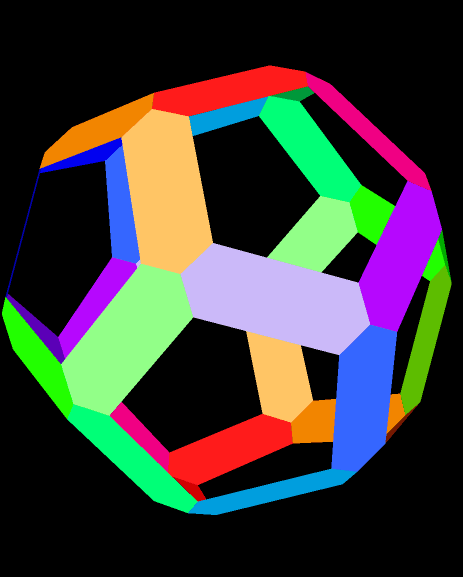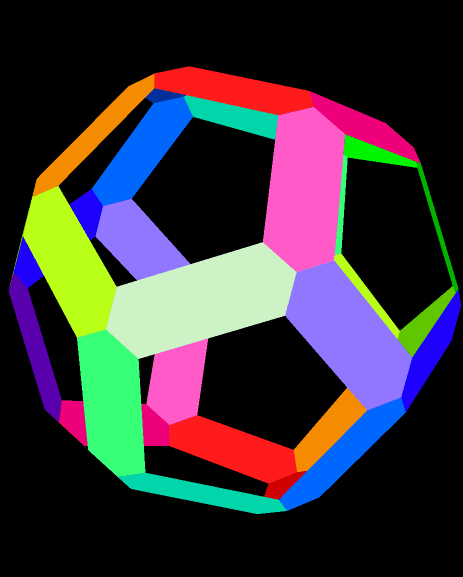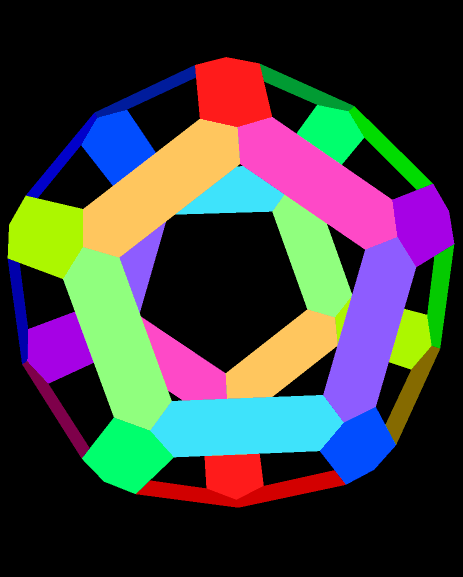
Software credit: see http://www.software3d.com/Stella.php to try or buy the software I used to make this. It’s called Stella 4d.
In each case, modifications along hexagon-edges were made using equilateral triangles. Every segment in this tessellation has equal length, also, which required trisection of the original hexagons’ sides.
RobertLovesPi.net 