The Twelfth Stellation of the Triakis Tetrahedron

Posted on 20 January 2015 by RobertLovesPi

Created with Stella 4d, available here.

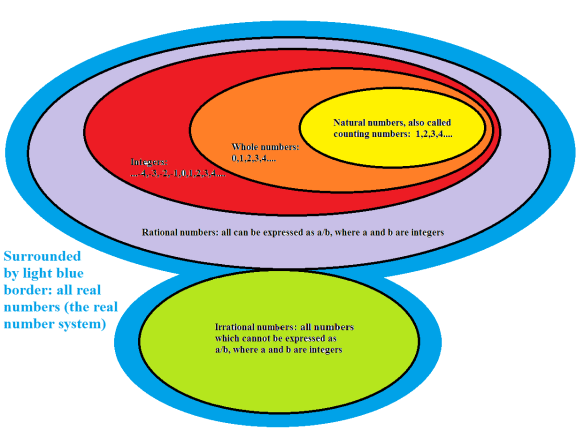
A Venn Diagram of the Real Number System

Posted on 19 January 2015 by RobertLovesPi

23-Tex: The Truncated 600-Cell

Posted on 19 January 2015 by RobertLovesPi

One of the regular 4-dimensional polytopes, or polychora, is called the 600-cell. If you truncate it, you get the figure above, called “23-tex” for short. Its unit cells are 600 truncated tetrahedra, as well as 120 icosahedra. As shown above, you see only the cells, with space between them so you can see them, and vertices and edges rendered invisible. If the vertices and edges are shown, though, 23-tex looks like this:

$23-Tex with$

Since these are four-dimensional figures, it’s not possible to see what these really look like all at once, in hyperspace, because you, the observer, are trapped in a universe where only three spatial dimensions are easy to perceive. That’s one reason I’m showing these figures with them rotating — as they spin, in hyperspace, the “slice” of the shape which appears as a three-dimensional projection, in our universe, changes. Over time, then, you get to see it all — but, in hyperspace, its appearance would be different. If you try to imagine a living creature living inside a horizontal Euclidean plane, and this creature trying to picture a three-dimensional shape, that can help with understanding the nature of the problem that arises when three-dimensional beings try to picture anything involving a fourth spatial dimension.

Three-dimensional polyhedra can be unfolded, and shown as flat “nets” made out of polygons. Well, what does the “net” of a four-dimensional polytope look like? The answer is one dimension “down” from four: the net is a bunch of three-dimensional polyhedra, stuck together at their faces, just as the nets of polyhedra are made of polygons joined at their edges. Here’s one possible net for 23-tex:

$23-Tex net$

The three images above were produced using Stella 4d: Polyhedron Navigator, software you may try for yourself, here.

A Euclidean Construction of a Golden Rectangle in Which All Circles Used Have Radius One or Two

Posted on 18 January 2015 by RobertLovesPi

There is more than one way to construct a golden rectangle using the Euclidean rules, but all the ones I have seen before use circles with irrational radii. This construction, which I believe to be new, does not use that shortcut, which helps explain its length. The cost of avoiding circles of irrational radius is decreased efficiency, as measured by the number of steps required for the entire construction.

In the diagram below, the distance between points A and B is set at one. All of the green circles have this radius, while the magenta circles have a radius exactly twice as long.

To make following the construction from the diagram above easier, I named the points in alphabetical order, as they appear, as the construction proceeds. The yellow rectangle is the resulting golden rectangle. The blue right triangle is what I used to get a segment with a length equal to the square root of five, which is a necessary step, given that this irrational number is part of the numerical definition of the exact value of the golden ratio (one-half of the sum of one and the square root of five). In order to make the hypotenuse have a length equal to the square root of five, by the Pythagorean Theorem, the two legs of this triangle have lengths of one and two.

The Golden Ratio: Working from a Definition to Find a Value

Posted on 18 January 2015 by RobertLovesPi

I found the image above through the Wikipedia article on the golden ratio. After using what appears above to define the golden ratio, the article then reveals its exact and approximate values. Later, the writers of the article do show the calculations involved in doing this, but they seem unnecessarily complicated. I’m going to try to simplify the process here, and might later edit/simplify this Wikipedia article to make it more understandable.

So, first, “a + b is to a as a is to b” need to be written as a fraction, which is easy enough: (a + b)/a = a/b. The value of this fraction, a/b, is, by definition, φ, the golden ratio. As an equation, this can be written a/b = φ.

Next, apply cross-multiplication to (a + b)/a = a/b, and it becomes (a + b)(b) = (a)(a), which simplifies to ab + b² = a².

Also, since a/b = φ, this means that a = φb (via the multiplication property). Next, ab + b² = a² is rewritten, with φb substituted for each a. The result of this substitution is (φb)(b) + b² = (φb)², which then becomes φb² + b² = φ²b². To simplify this, b² may be cancelled (via the division property), producing φ + 1 = φ². This may then be rearranged (via the subtraction and symmetric properties) to φ² – φ – 1 = 0. Two values of φ can then be found via the quadratic formula, and they are {1 ± sqrt[1 – (4)(1)(-1)]}/2 = [1 ± sqrt(5)]/2. Use “+,” and calculate a decimal approximation for this irrational number, and you get ~1.618, which is the golden ratio. Use “-” instead, and you get a negative number (approximately -0.618), which can be rejected on the grounds that a ratio of two lengths must be positive, since all lengths, themselves, are positive.

Also, I’m changing my mind regarding changing Wikipedia, on this subject. The two versions of the calculation (the one now on Wikipedia, and mine) don’t match, but both are mathematically valid — and, while my version makes more intuitive sense to me, that doesn’t mean it would make more sense to others, and Wikipedia isn’t there for me alone. Until I actually wrote the calculation out, I thought my version would be simpler, but I cannot claim that now.

[Later addition: see the first comment below for a way, suggested by a reader of this blog, to simplify the calculation, as I wrote it above. I’m not going to take credit for his improvement, of course — that would violate mathematical etiquette!]

The Rules of Cats

Posted on 17 January 2015 by RobertLovesPi

Jynx the Kitten may not be fully grown yet, but he certainly knows these rules.

All cats (and kittens) know these rules, and efforts, by anyone, to get cats (or kittens) to break them are futile.

(Photo credit: my wife took this picture, after Jynx decided she needed to take a break from crotcheting. When Jynx tries to floss his teeth with the yarn, that’s always disruptive.)

A Polyhedron Featuring Enneagons and Two Types of Pentagon

Posted on 16 January 2015 by RobertLovesPi

Enneagons are nine-sided polygons, and some people prefer to call them “nonagons.” I try not to use the latter term because it mixes Greek and Latin word-parts, which the former term, derived purely from Greek, does not do.

This was made using Stella 4d, a program you may try for yourself here.

Weaving Silk Online

Posted on 15 January 2015 by RobertLovesPi

The image above took very little time to make, online, at this website. The user interface there allows a large degree of control over the shapes and colors used in the images one produces. I didn’t notice a “save image” button, but that’s what screenshots are for, right?

A Short Short Story, Set In an Alternate Universe

Posted on 15 January 2015 by RobertLovesPi

Having run out of appeals, the famous actor bravely stood ready, as Queen Elizabeth II readied her ceremonial sword. Suddenly, a high-pitched voice from the gallery cried out, “Please, Your Majesty! Your Highness, please — anyone but Patrick Stewart! Spare him, and I will die in his place!”

Her heart moved by this young fan’s simple plea, the Queen slowly put down her sword. She carried out no executions that day, to the relief of millions of fans of Star Trek: The Next Generation, from all around the world. However, for the rest of his life, anyone who wanted to see Patrick Stewart had to visit the Tower of London to do so, during the limited hours of visitation permitted for guests of the prisoners there.

[Image credit: see this website.]