About RobertLovesPi

I go by RobertLovesPi on-line, and am interested in many things, a large portion of which are geometrical. Welcome to my own little slice of the Internet. The viewpoints and opinions expressed on this website are my own. They should not be confused with those of my employer, nor any other organization, nor institution, of any kind.

Not for Government Use

Posted on 17 March 2015 by RobertLovesPi

The Human Reaction, When Mathematics No Longer Seems to Make Sense: What Is This Sorcery?

Posted on 15 March 2015 by RobertLovesPi

Unless you understand all of mathematics — and absolutely no one does — there is a point, for each of us, where mathematics no longer makes sense, at least at that moment. Subjectively, this can make the mathematics beyond this point, which always awaits exploration, appear to be some form of sorcery.

Mathematics isn’t supernatural, of course, but this is a reaction humans often have to that which they do not understand. Human reactions do not require logical purpose, and they don’t always make sense — but there is always a reason for them, even if that reason is sometimes simply that one is utterly bewildered.

In my case, this is the history of my own reactions, as I remember them, to various mathematical concepts. The order used is as close as I can remember to the sequence in which I encountered each idea. The list is, of necessity, incomplete.

Counting numbers: no problem, but what do I call the next one after [last one I knew at that time]? And the next one? And the next? Next? Next? [Repeat, until everyone within earshot flees.]
Zero exists: well, duh. That’s how much of whatever I’m snacking on is left, after I’ve eaten it all.
Arithmetic: oh, I’m glad to have words for this stuff I’ve been doing, but couldn’t talk about before.
Negative numbers: um, of course those must exist. No, I don’t want to hear them explained; I’ve got this already. What, you want me to demonstrate that I understand it? Ok, can I borrow a dollar? Oh, sure, I’ll return it at some point, but not until after I’ve spent it.
Multiple digits, the decimal point, decimal places, place value: got it; let’s move on, please. (I’ve never been patient with efforts to get me to review things, once I understand them, on the grounds that review, under such conditions, is a useless activity.)
Pi: love at first sight.
Fractions: that bar means you divide, so it all follows from that. Got it. Say, with these wonderful things, why, exactly, do we need decimals, again? Oh, yeah, pi — ok, we keep using decimals in order to help us better-understand the number pi. That makes sense.
“Improper” fractions: these are cool! I need never use “mixed numbers” again (or so I thought). Also, “improper” sounds much more fun than its logical opposite, and I never liked the term “mixed numbers,” nor the way those ugly things look.
Algebra: ok, you turned that little box we used before into an “x” — got it. Why didn’t we just use an “x” to begin with? Oh, and you can do the same stuff to both sides of equations, and that’s our primary tool to solve these cool puzzles. Ok. Got it.
Algebra I class: why am I here when I already know all this stuff?
Inequality symbols: I’m glad they made the little end point at the smaller number, and the larger side face the larger number, since that will be pretty much impossible to forget.
Scientific notation: well, I’m glad I get to skip writing all those zeroes now. If only I knew about this before learning number-names, up to, and beyond, a centillion. Oh well, knowing those names won’t hurt me.
Exponents: um, I did this already, with scientific notation. Do not torture me with review of stuff I already know!
Don’t divide by zero: why not? [Tries, with a calculator]: say, is this thing broken? [Tries dividing by smaller and smaller decimals, only slightly larger than zero]: ok, the value of the fraction “blows up” as the denominator approaches zero, so it can’t actually get all the way there. Got it.
Nonzero numbers raised to the power of zero equal one: say what? [Sits, bewildered, until thinking of it in terms of writing the number one, using scientific notation: 1 x 10º.] Ok, got it now, but that was weird, not instantly understanding it.
Sine and cosine functions: got it, and I’m glad to know what those buttons on the calculator do, now, but how does the calculator know the answers? It can’t possibly have answers memorized for every millionth of a degree.
Tangent: what is this madness that happens at ninety degrees? Oh, right, triangles can’t have two right angles. Function “blows up.” Got it.
Infinity: this is obviously linked to what happens when dividing by ever-smaller numbers, and taking the tangent of angles approaching a right angle. I don’t have to call it “blowing up” any more. Ok, cool.
Factoring polynomials: I have no patience for this activity, and you can’t stop me from simply throwing the quadratic formula at every second-order equation I see.
Geometry (of the type studied in high school): speed this up, and stop stating the obvious all the time!
Radicals: oh, I was wondering what an anti-exponent would look like.
Imaginary numbers: well, it’s only fair that the negative numbers should also get square roots. Got it. However, Ms. _____________, I’d like to know what the square root of i is, and I’d like to know this as quickly as possible. (It took this teacher and myself two or three days to find the answer to this question, but find it we did, in the days before calculators would help with problems like this.)
The phrase “mental math” . . . um, isn’t all math mental? Even if I’m using a calculator, my mind is telling my fingers which buttons to press on that gadget, so that’s still a mental activity. (I have not yielded from this position, and therefore do not use the now-despised “mental math” phrase, and, each time I have heard it, to date, my irritation with the term has increased.)
0.99999… (if repeated forever) is exactly equal to one: I finally understood this, but it took attacks from several different directions to get there, with headaches resulting. The key to my eventual understanding it was to use fractions: ninths, specifically.
The number e, raised to the power of i‏π, equals -1: this is sorcery, as far as I can see. [Listens to, and attempts to read, explanations of this identity.] This still seems like sorcery!
What it means to take the derivative of an expression: am I just supposed to memorize this procedure? Is no one going to explain to me why this works?
Taking the derivative of a polynomial: ok, I can do this, but I don’t have the foggiest idea why I’m doing it, nor why these particular manipulations of one function give you a new function which is, at all points along the x-axis, the slope of the previous function. Memorizing a definition does not create comprehension.
Integral calculus: this gives me headaches.
Being handed a sheet of integration formulas, and told to memorize them: hey, this isn’t even slightly fun anymore. =(
Studying polyhedra: I finally found the “sweet spot” where I can handle some, but not all, of the puzzles, and I even get to try to find solutions in ways different from those used by others, without being chastised. Yay! Math is fun again! =)
Realizing, while starting to write this blog-post, that you can take the volume of a sphere, in terms of the radius, (4/3)πr³, take its derivative, and you get the surface area of the same sphere, 4πr²: what is this sorcery known as calculus, and how does it work, so it can stop looking like sorcery to me?

Until and unless I experience the demystification of calculus, this blog will continue to be utterly useless as a resource in that subfield of mathematics. (You’ve been warned.) The primary reason this is so unlikely is that I haven’t finished studying (read: playing with) polyhedra yet, using non-calculus tools I already have at my disposal. If I knew I would live to be 200 years old, or older, I’d make learning calculus right now a priority, for I’m sure my current tools’ usefulness will become inadequate in a century or so, and learning calculus now, at age 47, would likely be easier than learning it later. As things are, though, it’s on the other side of the wall between that which I understand, and that which I do not: the stuff that, at least for now, looks like magic — to me.

Please don’t misunderstand, though: I don’t “believe in” magic, but use it simply as a label of convenience. It’s a name for the “box ,” in my mind, where ideas are stored, but only if I don’t understand those ideas on first exposure. They remain there until I understand them, whether by figuring the ideas out myself, or hearing them explained, and successfully understanding the explanation, at which point the ideas are no longer thought of, on any level, as “magic.”

To empty this box, the first thing I would need would be an infinite amount of time. Once I accepted the inevitability of the heat death of the universe, I was then able to accept the fact that my “box of magic” would never be completely emptied, for I will not get an infinite amount of time.

[Image credit: I made a rainbow-colored version of the compound of five cubes for the “magic box” picture at the top of this post, using Stella 4d, a program you may try here.]

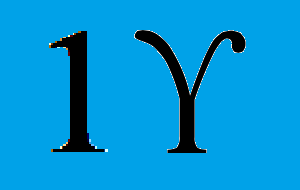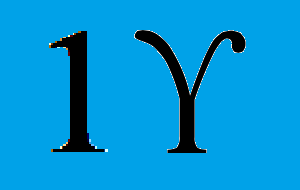
My Early Play with Informal Numbers, Such as Umpteen: A Look at Early Development of a Special Interest in a Young Person with Asperger’s

Posted on 13 March 2015 by RobertLovesPi

As a young child (before I started school), my strong interest in mathematics was always there. No one knew I had Asperger’s at that time, but it is clear to me now, in retrospect, that I was a young “Aspie,” in the early stages of the development of a special interest.

I cannot remember a time without my math-fascination, to the point where I speculate that I was motivated to learn to talk, read, and write English simply to bring more of the mathematics in my head into forms which I could express, and also to gain the ability to research forms of mathematics, by reading about them, which were new to me: negative numbers, fractions, names for extremely large numbers, and so on. I would devour one concept, internalize it, so it could not be forgotten, and quickly move on to my next mathematical “snack.” The shift to geometry-specialization took many years longer; at first, my special interest was simply mathematics in general, to the extent that I could understand it.

I was too young, then, to even understand the difference between actual numbers, and informal numbers I heard others use in conversation, such as zillion, jillion, and especially umpteen, and, armed with this lack of understanding, I endeavored to figure out the properties of these informal numbers. Zillion and jillion were uncountably large: that much seemed clear, although I could never figure out which one was larger. Umpteen, however, seemed more accessible, due to the “-teen” prefix. It seemed perfectly reasonable to me to simplify umpteen to a more fundamental informal number, “ump,” simply by subtracting ten from umpteen, following the pattern I had noticed which connects thirteen to three, seventeen to seven, and so on. This led to the following:

1ϒ – 10 = ϒ (umpteen minus ten equals ump)

I wasn’t using upsilon as a symbol for the informal number “ump” at that age. Rather, I simply needed a symbol, today, to write this blog-post, so I chose one. The capital Greek letter upsilon seems like a good pick. I’m using it more like a digit, here, rather than a variable — although, when I first reasoned this out, over forty years ago, I had not yet learned to distinguish between digits, variables, and numbers, at least not using other peoples’ terms.

Occasionally, I would hear people use ump-based informal numbers (I grew up in Arkansas, you see) which clearly seemed larger than umpteen. One such “number” I heard was, of all things, “umpty-ump.” Well, just how large is umpty-ump? I reasoned that it had to be umpteen minus ten, with this difference then multiplied by eleven.

1ϒ – 10 = ϒ (umpteen minus ten equals ump)

10(ϒ) = ϒ0 (ten times ump equals umpty)

ϒ0 + ϒ = ϒϒ (umpty plus ump equals umpty-ump)

Factoring ump out of the third equation above yields the following:

ϒ(10 + 1) = ϒ(11)

Next, ump cancels on both sides, leaving the following, which is known to be true without the involvement of informal numbers:

10 + 1 = 11

Having figured this out, I would then explain it, at great length, to anyone who didn’t make their escape quickly enough. It never occurred to me, at that age, that there actually are people who do not share my intense interest in mathematics. (Confession: I still do not understand the reason for the shockingly small amount of interest, in mathematics, found in the minds of most people. Why doesn’t everyone find math fascinating, since, well, it is fascinating?)

What I didn’t yet realize is that I was actually figuring out important concepts, with this self-motivated mathematical play: place value in base-ten, doing calculations in my head, some basic algebra, and, of course, the fact that playing with numbers is ridiculously fun. (That last one is a fact, by the way — just in case there is any doubt.)

I did not distinguish play from work at that age, and considered any interruption absolutely unacceptable. This is what I would typically say, if anyone, including my parents, disturbed me while I was working these things out, but was not yet ready to discuss them: “I’m BUSY!”

Everyone who knew me then, I am guessing, remembers me shouting this, as often as I found it necessary.

Some Stereotypes Are Based on Reality (with Jynx the Kitten)

Posted on 5 March 2015 by RobertLovesPi

The Second of Dave Smith’s “Bowtie” Polyhedral Discoveries, and Related Polyhedra

Posted on 5 March 2015 by RobertLovesPi

Dave Smith discovered the polyhedron in the last post here, shown below, with the faces hidden, to reveal how the edges appear on the back side of the figure, as it rotates. (Other views of it may be found here.)

So far, all of Smith’s “bowtie” polyhedral discoveries have been convex, and have had only two types of face: regular polygons, plus isosceles trapezoids with three equal edge lengths — a length which is in the golden ratio with that of the fourth side, which is the shorter base.

He also found another solid: the second of Smith’s polyhedral discoveries in the class of bowtie symmetrohedra. In it, each of the four pentagonal faces of the original discovery is augmented by a pentagonal pyramid which uses equilateral triangles as its lateral faces. Here is Smith’s original model of this figure, in which the trapezoids are invisible. (My guess is that these first models, pictures of which Dave e-mailed to me, were built with Polydrons, or perhaps Jovotoys.)

With Stella 4d (available here), the program I use to make all the rotating geometrical pictures on this blog, I was able to create a version (by modifying the one created by via collaboration between five people, as described in the last post) of this interesting icositetrahedron which shows all four trapezoidal faces, as well as the twenty triangles.

Here is another view: trapezoids rendered invisible again, and triangles in “rainbow color” mode.

It is difficult to find linkages between the tetrapentagonal octahedron Smith found, and other named polyhedra (meaning I haven’t yet figured out how), but this is not the case with this interesting icositetrahedron Smith found. With some direct, Stella-aided polyhedron-manipulation, and a bit of research, I was able to find one of the Johnson solids which is isomorphic to Smith’s icositetrahedral discovery. In this figure (J90, the disphenocingulum), the trapezoids of this icositetrahedron are replaced by squares. In the pyramids, the triangles do retain regularity, but, to do so, the pentagonal base of each pyramid is forced to become noncoplanar. This can be difficult to see, however, for the now-skewed bases of these four pyramids are hidden inside the figure.

Both of these solids Smith found, so far (I am confident that more await discovery, by him or by others) are also golden polyhedra, in the sense that they have two edge lengths, and these edge lengths are in the golden ratio. The first such polyhedron I found was the golden icosahedron, but there are many more — for example, there is more than one way to distort the edge lengths of a tetrahedron to make golden tetrahedra.

To my knowledge, no ones knows how many golden polyhedra exist, for they have not been enumerated, nor has it even been proven, nor disproven, that their number is finite. At this point, we simply do not know . . . and that is a good way to define areas in mathematics in which new work remains to be done. A related definition is one for a mathematician: a creature who cannot resist a good puzzle.

The First of Dave Smith’s “Bowtie” Polyhedral Discoveries: An Example of Mathematical Collaboration

Posted on 2 March 2015 by RobertLovesPi

Recently, a reader of this blog contacted me about a polyhedron he wished to model. His name is Dave Smith, and he had already done much of the work involved, but needed help finishing off his project. Here’s the picture he e-mailed me.

The visible faces are regular pentagons — four of them. The invisible faces are isosceles trapezoids, in two “bowtie” pairs which share their shortest edges with those of their reflections. I e-mailed Smith, and told him the truth: I didn’t have a clue how to make this in Stella 4d, the program I use to make the rotating polyhedra on this blog (including the one below). I also told him I wasn’t giving up — merely enlisting help with his puzzle.

And, with that, I went to Facebook, posting the image above, along with an explanation, and request for help finishing it. This may not be what most people think of when they consider Facebook, but I have deliberately sought out experts there in many fields, including geometry, to make the social-networking site useful in unusual ways, such as getting help with geometrical puzzles I can’t solve alone. Three geometricians with skills which exceed mine (Wendy Krieger, Tom Ruen, and Robert Webb, who wrote Stella 4d) began discussing the figure. One of them, Tom Ruen, sent me .stel files (That’s what Stella 4d uses) for multiple figures, getting closer each time. With the last such virtual model Tom sent me, I was able to “tweak” it to get the pentagons regular.

This eight-faced figure has two edge lengths, the shorter appearing only twice, as the shared, shorter base within each “bowtie” pair of isosceles trapezoids — and these two edge lengths are in the golden ratio. A type of octahedron, it also has an interesting form of symmetry — it reminds me of pyritohedral symmetry, but is not; the features seen in pyritohedral symmetry in relation to the x-, y-, and z-axes of coordinate space only show up here in relation to two of these three axes. This symmetry-form is called dihedral symmetry.

And it only took five people to figure all of this out!

When the Westboro Baptist Church Protests Leonard Nimoy’s Funeral, What Is the Appropriate Phaser Setting?

Posted on 1 March 2015 by RobertLovesPi

I’ve been trying to determine the appropriate phaser setting for dealing with these people, and have decided to go with “heavy stun.”

Heavy stun is kinder than the WBC adults deserve, but some of those WBC people are infants and children, and they have a chance of throwing off their brainwashing as they grow up. I would not deny them that chance.

[Photo credit: This website is where I found this image. It’s a story about the WBC announcing their intent to protest Leonard Nimoy’s funeral.]

A Polyhedron with 542 Faces

Posted on 28 February 2015 by RobertLovesPi

I used Stella 4d to make this. This program’s name, in the last sentence, is a link; if you follow it, you’ll be taken to a site where you can give it a try for free.

5, 10, and 15 (from 2012)

Posted on 27 February 2015 by RobertLovesPi

I recently found a bunch of my “lost” geometrical art which never found its way to this blog before, and here’s the latest piece of it. Created in 2012, it has a central pentadecagon, five orange decagons partially hidden behind other polygons, and many pentagons, all of them regular.

Nine (2015) / Nine (2013)

Posted on 23 February 2015 by RobertLovesPi

First, the newer version I just made:

Next, the 2013 version, which I recently found, along with a bunch of other previously-lost stuff from around then. The two are simply color-inversions of each other, according to the rules for color-inversion used by MS-Paint.